Retos de la semana 50 de 2025
Nivel 1. Se consideran las funciones $f:\mathbb{R}\to\mathbb{R}$ de la forma $f(x)=ax+b$, siendo $a$ y $b$ números reales. ¿Para qué valores de a y b se verifica $f^{2000}(x) = x$ para todo número real $x$.
Nota: Se define $f^2(x)=f(f(x))$, $f^3(x)=f(f(f(x)))$ y, en general, $f^n(x) = f(f^{n-1}(x))$.
Nivel 2. Sea $ABC$ un triángulo con $AB\lt AC$ y sea $I$ su incentro. La circunferencia inscrita en $ABC$ es tangente al lado $BC$ en el punto $D$. Sea $E$ el único punto que satisface que $D$ es el punto medio del segmento $BE$. La línea perpendicular a $BC$ que pasa por $E$ corta a $CI$ en el punto $P$. Demostrar que $BP$ es perpendicular a $AD$.
Retos de la semana 49 de 2025
Halla el producto de tres números primos $p,q,r$, sabiendo que:
\[\left\{\begin{array}{l}r - q = 2p,\\ rq + p^2 = 676.\end{array}\right.\]
pistasolución 1info
Pista. Demuestra en primer lugar que $(p+q)^2=676$.
Solución. Sustituyendo $r=2p+q$ en la segunda ecuación nos queda $676=(2p+q)q+p^2=(p+q)^2$, luego tiene que ser $p+q=26$. Las formas de expresar $26$ como suma de dos primos son
\[26=3+23=7+19=13+13=19+7=23+3\]
y de todas ellas la única que cumple que $r=2p+q$ es primo es $p=3$ y $q=23$, con lo que $r=29$. El producto que nos piden es $pqr=3\cdot 23\cdot 29=2001$ (¡el año!).
Demostrar la igualdad
\[\binom{n}{0}^2+\binom{n}{1}^2+\ldots+\binom{n}{n}^2=\binom{2n}{n}.\]
pistasolución 1solución 2info
Pista. Desarrolla por el binomio de Newton ambos miembros de la igualdad
\[(x+1)^{2n}=(x+1)^n(x+1)^n.\]
Solución. El número $\binom{2n}{n}$ aparece en el binomio de Newton
\[(x+1)^{2n}=\textstyle\binom{2n}{0}x^{2n}+\binom{2n}{1}x^{2n-1}+\ldots+\binom{2n}{n}x^n+\ldots+\binom{2n}{2n},\]
siendo el coeficiente del término de grado $n$. Sin embargo, podemos expresar también $(x+1)^{2n}=(x+1)^n(x+1)^n$ y desarrollar esto último de nuevo por la fórmula de Newton:
\[(x+1)^{2n}=\textstyle\left(\binom{n}{0}x^{n}+\binom{n}{1}x^{n-1}+\ldots+\binom{n}{n}\right)\left(\binom{n}{0}x^{n}+\binom{n}{1}x^{n-1}+\ldots+\binom{n}{n}\right).\]
En esta última ecuación, el término de grado $n$ viene dado por
\[\binom{2n}{n}=\binom{n}{0}\binom{n}{n}+\binom{n}{1}\binom{n}{n-1}+\ldots+\binom{n}{n}\binom{n}{0}.\]
Teniendo en cuenta que $\binom{n}{k}=\binom{n}{n-k}$, se llega directamente a la fórmula del enunciado.
Solución. Vamos a utilizar que $\binom{2n}{n}$ es el número de formas de elegir $n$ elementos del conjunto $C=\{1,2,3,\ldots,2n\}$. Si descomponemos este conjunto en los conjuntos $A=\{1,2,\ldots,n\}$ y $B=\{n+1,n+2,\ldots,2n\}$, elegir $n$ elementos de $C$ equivale a elegir $k$ elementos de los $n$ que tiene $A$ y $n-k$ elementos de los $n$ que tiene $B$, pero esto debe hacerse para cualquier $k$ desde $0$ hasta $n$, lo que nos dice que
\[\binom{2n}{n}=\sum_{k=0}^n\binom{n}{k}\binom{n}{n-k}=\sum_{k=0}^n\binom{n}{k}^2,\]
donde hemos usado que $\binom{n}{k}=\binom{n}{n-k}$ para todo $k$.
Retos de la semana 48 de 2025
Se considera el conjunto $C$ de todos los vectores de $r$ componentes, cada una de las cuales es igual a $1$ o $-1$. Calcular la suma de todas las componentes de todos los elementos de $C$ excluyendo al vector $(1,1,\ldots,1)$.
pistasolución 1solución 2info
Pista. Empareja los vectores de forma creativa.
Solución. Podemos agrupar cada vector con el que resulta de cambiar todas sus componentes de signo, lo cual nos da suma $0$. Esto funciona salvo por el caso del vector $(-1,-1,\ldots,-1)$ que se ha quedado sin pareja al excluir el $(1,1,\ldots,1)$ explícitamente en el enunciado. Por lo tanto, la suma que nos piden es $-r$.
Solución. Para cada entero $0\leq k\leq r$ hay exactamente $\binom{r}{k}$ vectores con $k$ componentes iguales a $1$ y las otras $r-k$ iguales a $-1$. Por lo tanto, cada uno de tales vectores tendrá una suma $k-(r-k)=2k-r$ y la suma que nos piden es
\[\sum_{k=0}^{r-1}(2k-r)\binom{r}{k}=2\sum_{k=0}^{r-1}k\binom{r}{k}-r\sum_{k=0}^{r-1}\binom{r}{k}=2\sum_{k=0}^{r-1}k\binom{r}{k}-r(2^r-1).\]
Observemos que hemos tenido que eliminar el sumando $k=r$ ya que en el enunciado se nos pide excluir explícitamente el vector $(1,1,\ldots,1)$. También hemos usado que la suma de la fila $k$-ésima del triángulo de Pascal es igual a $2^r$. Ahora bien, para tratar la sumatoria que queda, escribamos
\begin{align*}
\sum_{k=0}^{r-1}k\binom{r}{k}&=\sum_{k=1}^{r-1}\frac{k\cdot r!}{k!(r-k)!}=\sum_{k=1}^{r-1}\frac{r!}{(k-1)!(r-k)!}=r\sum_{k=1}^{r-1}\frac{(r-1)!}{(k-1)!((r-1)-(k-1))!}\\
&=r\sum_{k=0}^{r-2}\frac{(r-1)!}{k!((r-1)-k)!}=r\sum_{k=0}^{r-2}\binom{r-1}{k}=r(2^{r-1}-1),
\end{align*}
ya que hemos tenido que excluir de nuevo el sumando $k=r-1$. Por lo tanto, volviendo al cálculo original, la solución al problema es
\[\sum_{k=0}^{r-1}(2k-r)\binom{r}{k}=2r(2^{r-1}-1)-r(2^r-1)=-r.\]
Sea $a$ un entero positivo impar mayor que $17$ tal que $3a-2$ es un cuadrado perfecto. Demostrar que existen enteros positivos distintos $b$ y $c$ tales que $a+b$, $b+c$, $a+c$ y $a+b+c$ son cuatro cuadrados perfectos.
pistasolución 1info
Pista. Prueba a tomar $b$ y $c$ como expresiones que dependen de $a$. Por ejemplo, puedes comenzar probando con $b=2a-2$, para que $a+b=3a-2$ sea un cuadrado perfecto.
Solución. Escribamos $3a-2=m^2$ para cierto entero positivo $m$. De esta definición se deduce fácilmente que $m$ no es múltiplo de $3$ y, como $a$ es impar, se tiene también que $m$ es impar. En otras palabras, $m$ es congruente con $1$ ó con $5$ módulo $6$. El hecho de que $a\gt 17$ se traduce en que $m^2\gt 49$. Consideremos entonces los números
\[b=\frac{2(m^2-1)}{3},\qquad c=\frac{(m^2-25)(m^2-1)}{36}.\]
Es fácil probar que son enteros por ser $m$ congruente con $1$ ó con $5$ módulo $6$, y son positivos por ser $m\gt 49$. Además,
\[c-b=\frac{(m^2-25)(m^2-1)}{36}-\frac{24(m^2-1)}{36}=\frac{(m^2-49)(m^2-1)}{36}\gt 0,\]
lo que nos dice que $b\neq c$. Veamos finalmente que cumplen la propiedad sobre los cuadrados.
\begin{align*}
a+b&=\frac{m^2+2}{3}+\frac{2(m^2-1)}{3}=m^2,\\
b+c&=\frac{2(m^2-1)}{3}+\frac{(m^2-25)(m^2-1)}{36}=\left(\frac{m^2-1}{6}\right)^2,\\
a+c&=\frac{m^2+2}{3}+\frac{(m^2-25)(m^2-1)}{36}=\left(\frac{m^2-7}{6}\right)^2,\\
a+b+c&=\frac{m^2+2}{3}+\frac{2(m^2-1)}{3}+\frac{(m^2-25)(m^2-1)}{36}=\left(\frac{m^2+5}{6}\right)^2.
\end{align*}
Nota. Hemos escrito todos los resultados en función de $m^2$, aunque podríamos haberlo hecho en función de $a$ (el único motivo era que se vea de forma explícita que todas las sumas son cuadrados):
\[b=2a-2,\qquad c=\frac{(a-9)(a-1)}{4},\]
con lo que
\[
a+b=3a-2,\quad
b+c=\left(\frac{a-1}{2}\right)^2,\quad
a+c=\left(\frac{a-3}{2}\right)^2,\quad
a+b+c=\left(\frac{a+1}{2}\right)^2.
\]
Retos de la semana 47 de 2025
- Encontrar todos los enteros positivos $n$ tales que $2^n-1$ es divisible entre $7$.
- Demostrar que no hay enteros positivos $n$ tales que $2^n+1$ es divisible entre $7$.
pistasolución 1info
Pista. Observa que el resto de dividir $2^n$ entre $7$ va variando cíclicamente.
Solución. Escribiéndolo de otra manera, queremos encontrar todos los $n\in\mathbb{N}$ tales que $2^n\equiv 1\ (\mbox{mód } 7)$. Ahora bien, como $2^3=8\equiv 1\ (\mathrm{mod}\ 7)$, tenemos que:
- Si $n=3k$, entonces $2^{3k}=(2^3)^k\equiv 1\ (\mathrm{mod}\ 7)$.
- Si $n=3k+1$, entonces $2^n=2\cdot (2^3)^k\equiv 2\ (\mathrm{mod}\ 7)$.
- Si $n=3k+2$, entonces $2^n=4\cdot(2^3)^k\equiv 4\ (\mathrm{mod}\ 7)$.
Por tanto, los únicos valores de $n$ para los que $2^n-1$ es múltiplo de $7$ son los múltiplos de 3. Sin embargo, no hay valores de $n$ para los que $2^n+1$ sea múltiplo de $7$ ya que esto muestra que $2^n+1$ es congruente con $2$, $3$ o $5$ módulo $7$.
Se considera una función $f:\mathbb{N}\to\mathbb{N}$ que verifica las siguientes propiedades:
- $f(2n) = f(2n + 1) + 1$,
- $f(2n + 1) f(2n + 2) = 4n^2 + 6n$,
- $f(2020) = 2021$.
Determina la expresión de $f$, esto es, $f(n)$ para cada $n\in\mathbb{N}$.
pistasolución 1info
Pista. Observa que $4n^2+6n=2n(2n+3)$ y asigna uno de los factores a $f(2n+1)$ y otro a $f(2n+2)$ para obtener una expresión (muy sencilla) para $f(n)$ distinguiendo si $n$ es par o impar. Luego solo hay que ver que hay una única función que cumple las tres condiciones (a), (b) y (c).
Solución. Observando la factorización $4n^2+6n=2n(2n+3)$, es muy fácil encontrar la siguiente función y ver que cumple las tres condiciones:
\[f(n)=\begin{cases}
n+1&\text{si }n\text{ es par,}\\
n-1&\text{si }n\text{ es impar.}
\end{cases}\]
Vamos a probar que solo hay una función con las condiciones dadas, luego esta será la única. La condición (a) nos asegura que el valor de $f(n)$ para $n$ par determina los valores para $n$ impar. Además, nos permite reescribir las condiciones (b) y (c) como
\[(f(2n)-1)f(2n+2)=4n^2+6n,\qquad f(2020)=2021.\]
Está claro entonces que $f(2n)$ determina el valor de $f(2n+2)$ para todo $n\in\mathbb{N}$, luego $f(2020)$ determina el valor en todos los números pares mayores que $2020$. También $f(2n+2)$ determina el valor de $f(2n)$, luego $f(2020)$ determina el valor de $f$ en todos los pares menores que $2020$. Todo esto nos dice que hay una única función en esas condiciones.
Retos de la semana 46 de 2025
Sean $x,y,z$ números reales positivos.
- Si $x+y+z\geq 3$, ¿se verifica necesariamente que $\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\leq 3$?
- Si $x+y+z\leq 3$, ¿se verifica necesariamente que $\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\geq 3$?
pistasolución 1info
Pista. Utiliza la desigualdad entre las medias aritmética y armónica.
Solución. La respuesta al apartado (a) es negativa. Por ejemplo, los números $x=1$, $y=\frac{1}{2}$ y $z=\frac{3}{2}$ cumplen $x+y+z=3$, pero $\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=\frac{11}{3}\gt 3$.
La respuesta al apartado (b) es afirmativa. Para verlo, usamos la desigualdad entre las medias aritmética y armónica aplicada a los tres números positivos $x,y,z$:
\[\frac{3}{\frac{1}{x}+\frac{1}{y}+\frac{1}{z}}\leq \frac{x+y+z}{3}\leq 1\ \Longleftrightarrow\ \frac{1}{x}+\frac{1}{y}+\frac{1}{z}\geq 3.\]
Problema 418
Se considera un triángulo cuyos lados son los lados de un pentágono, hexágono y decágono regulares inscritos en circunferencias de radio unidad. Demostrar que dicho triángulo es rectángulo.
pistasolución 1solución 2info
Pista. Si $\ell_5$ es el lado del pentágono y $\ell_{10}$ es el lado del decágono, demuestra que $\ell_5^2=1+\ell_{10}^2$. El hecho de que $\ell_5$ también sea la longitud de una diagonal del decágono puede ayudarte.
Solución. El lado de un polígono de $n$ lados inscrito en una circunferencia de radio unidad viene dado por $2\sin(\frac{\pi}{n})$, luego el triángulo que estamos buscando tiene por lados $2\sin(\frac{\pi}{10})$, $2\sin(\frac{\pi}{6})=1$ y $2\sin(\frac{\pi}{5})$. El triángulo existirá y será rectángulo cuando estos tres números cumplan el teorema de Pitágoras. Como $2\sin(\frac{\pi}{10})$ es el mayor de los tres lados, tendrá que jugar el papel de la hipotenusa, es decir, el problema se reduce a demostrar que
\[4\sin^2\left(\frac{\pi}{5}\right)=1+4\sin^2\left(\frac{\pi}{10}\right).\]
Hay muchas formas de demostrar esta identidad usando trigonometría. Aquí comenzaremos calculando $\sin(\frac{\pi}{10})$ usando un pentágono regular $A_1A_2A_3A_4A_5$ de lado $\ell$ y diagonal $d$. Como $\angle A_4A_1A_3=\frac{\pi}{5}$, si tomamos $M$ el punto medio del lado $A_3A_4$, entonces $\angle A_4A_1M=\frac{\pi}{10}$ y el triángulo $A_4A_1M$ tiene un ángulo recto en $M$, luego $2\sin(\frac{\pi}{10})=2\frac{A_4M}{A_1A_4}=\frac{\ell}{d}$. Ahora bien, $\ell$ y $d$ satisfacen la relación $d^2=\ell^2+\ell d$ (véase la nota más abajo), luego $(\frac{\ell}{d})^2+\frac{\ell}{d}-1=0$, es decir, $2\sin(\frac{\pi}{10})$ es solución de la ecuación $x^2+x-1=0$. Resolviendo esta ecuación y quedándonos con la solución positiva, tenemos que
\[\sin\left(\frac{\pi}{10}\right)=\frac{-1+\sqrt{5}}{4}.\]
Usando ahora la fórmula del ángulo doble y la identidad $\sin^2(\frac{\pi}{10})+\cos^2(\frac{\pi}{10})=1$, podemos calcular
\[\sin^2\left(\frac{\pi}{5}\right)=4\sin^2\left(\frac{\pi}{10}\right)\cos^2\left(\frac{\pi}{10}\right)=4\left(\frac{-1+\sqrt{5}}{4}\right)\left(1-\left(\frac{-1+\sqrt{5}}{4}\right)^2\right)=\frac{5-\sqrt{5}}{8}.\]
Ahora podemos calcular explícitamente
\[4\sin^2\left(\frac{\pi}{5}\right)-4\sin^2\left(\frac{\pi}{10}\right)=\frac{5-\sqrt{5}}{2}-4\left(\frac{-1+\sqrt{5}}{4}\right)^2=\frac{5-\sqrt{5}}{2}-\frac{3-\sqrt{5}}{2}=1.\]
Nota. Hay varias formas de probar la identidad $d^2=\ell^2+\ell d$. Dos de ellas son las siguientes:
- Si $P$ denota la intersección de $A_1A_3$ y $A_2A_5$, entonces los triángulos $A_1A_4A_3$ y $A_3PA_2$ son semejantes (tienen los lados paralelos) y la relación $\frac{A_3A_4}{A_2P}=\frac{A_1A_4}{A_2A_3}$ se traduce en $\frac{\ell}{d-\ell}=\frac{d}{\ell}$, de donde $d^2=\ell^2+\ell d$.
- Otra forma de probarla es aplicar el teorema de Ptolomeo al cuadrilátero cíclico $A_1A_2A_3A_4$. El producto de sus diagonales es $d^2$ y la suma de los productos de lados opuestos es $\ell^2+\ell d$, de donde se deduce inmediatamente que $d^2=\ell^2+\ell d$.
Solución. Sea $A_1A_2\ldots A_{10}$ un decágono regular inscrito en una circunferencia de radio $1$, luego $A_1A_3A_5A_7A_9$ es un pentágono regular inscrito en la misma circunferencia. Si llamamos $\ell_5$ y $\ell_{10}$ a las longitudes de los lados del pentágono y el decágono, respectivamente, tendremos que demostrar que $\ell_{5}^2=1+\ell_{10}^2$ (observemos que el hexágono regular inscrito en esta circunferencia tiene lado igual al radio (igual a $1$).
El teorema de Ptolomeo nos dice que en un cuadrilátero cíclico el producto de las diagonales es igual a la suma de los productos de los lados opuestos. Por tanto,
- aplicándolo al cuadrilátero $A_1A_3A_5A_7$, obtenemos que $d^2=\ell_5^2-\ell_5 d$, siendo $d$ la diagonal del pentágono;
- aplicándolo al cuadrilátero $A_1A_5A_6A_7$, obtenemos que $\ell_5=\ell_{10}d$, luego $d=\frac{\ell_5}{\ell_{10}}$.
Sustituyendo $d=\frac{\ell_5}{\ell_{10}}$ en $d^2=\ell_5^2-\ell_5 d$, tenemos que
\[\frac{\ell_5^2}{\ell_{10}^2}=\ell_5^2-\frac{\ell_5^2}{\ell_{10}}\quad\Leftrightarrow\quad \ell_{10}^2=1+\ell_{10}.\]
El teorema de Pitágoras aplicado al triángulo rectángulo $A_1A_6A_7$ nos dice que $d^2+\ell_{10}^2=4$. Sustituyendo $d=\frac{\ell_5}{\ell_{10}}$ y usando repetidamente la relación $\ell_{10}^2=1+\ell_{10}$, obtenemos finalmente que
\[\ell_5^2=\ell_{10}^2(4-\ell_{10}^2)=(1+\ell_{10})(3-\ell_{10})=3+2\ell_0-\ell_{10}^2=3+2(\ell_0^2-1)-\ell_{10}^2=\ell_{10}^2+1.\]
Retos de la semana 45 de 2025
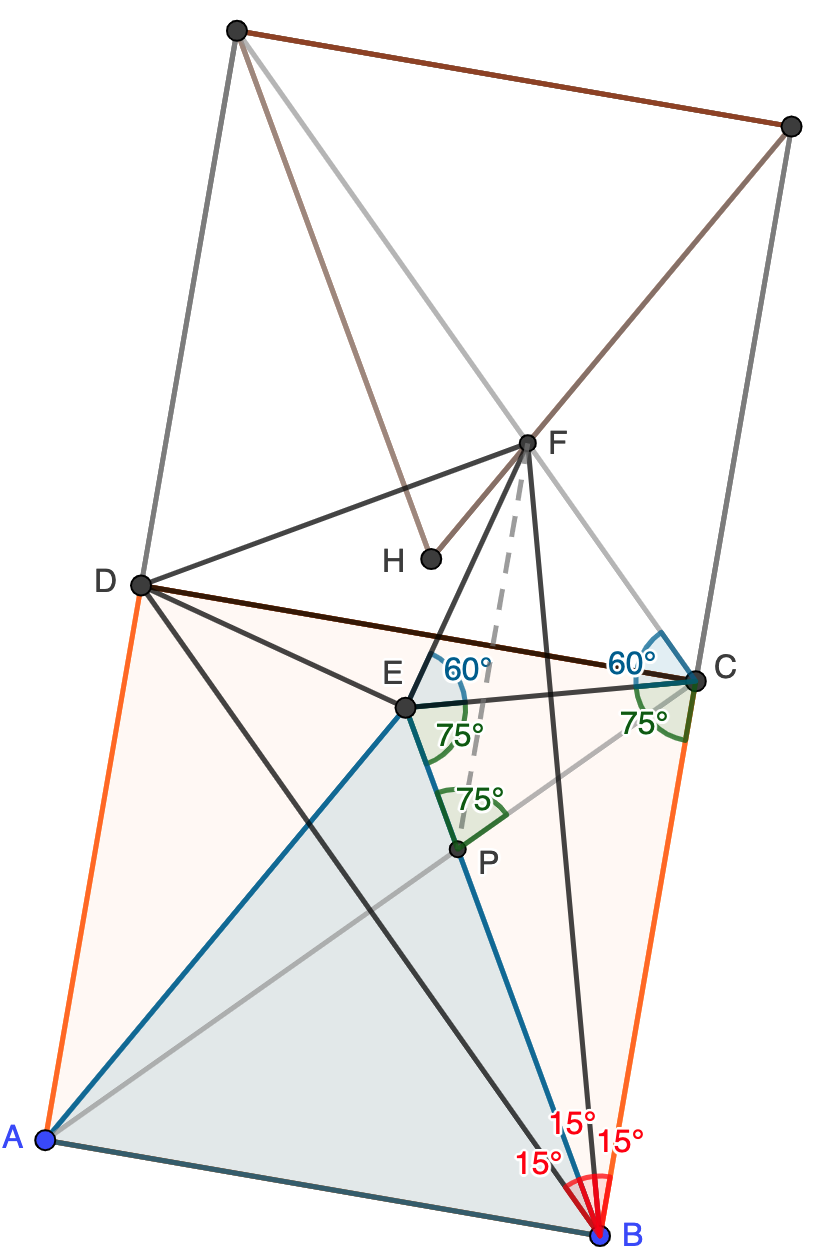
En el interior de un cuadrado $ABCD$ se construye el triángulo equilátero $ABE$. Sea $P$ el punto intersección de las rectas $AC$ y $BE$. Sea $F$ el punto simétrico de $P$ respecto de la recta $DC$. Se pide demostrar que:
- El triángulo $CEF$ es equilátero.
- El triángulo $DEF$ es rectángulo e isósceles.
- El triángulo $BDF$ es isósceles.
- El triángulo $PDF$ es equilátero.
pistasolución 1info
Pista. ¡Caza de ángulos!
Solución. El triángulo $ECB$ es isósceles ya que tiene dos de sus lados iguales a los lados del cuadrado $ABCD$. Como $\angle EBC=90-60=30$, tenemos que $\angle BEC=\angle ECB=75$ (para que los ángulos de este triángulo sumen $180$). Esto nos dice que $\angle DCE=90-75=15$, con lo que $\angle FCE=15+45=60$. Ahora bien, también tenemos que $\angle EPC=\angle APB=180-\angle PAB-\angle PBA=180-60-45=75$, luego $PCE$ es un triángulo isósceles. Tenemos así que $CP=EC$, pero también tenemos que $CP=CF$ por simetría, luego $CEF$ es equilátero por tener dos lados iguales que forman un ángulo igual a $60$. Hemos respondido así al apartado (a).
Que $CEF$ es equilátero implica que $EF=CE=DE$, ya que $CDE$ es claramente isósceles. Además, esto último nos dice que $\angle DEF=180-15-15=150$, con lo que $\angle DEF=150-60=90$. Tenemos entonces probado el apartado (b): $DEF$ es rectángulo e isósceles porque tiene dos lados iguales que forman un ángulo recto.
Ahora observamos que $\angle DEB=60+75=\angle FEB$, luego la recta $EB$ es la bisectriz interior del ángulo recto $\angle DEF$. Esta bisectriz es mediatriz del triángulo isósceles $DEF$, luego cualquier punto de $BE$ está a la misma distancia de $D$ que de $F$. En particular, el triángulo $BDF$ es isósceles y ya tenemos (c).
Tenemos que $PDF$ es isósceles por el mismo motivo, luego será suficiente ver que $\angle DFP=60$ y habremos terminado (hay realmente muchas formas de hacerlo). Como $\angle DBE=60-45=15$, tenemos que $\angle EBF=15$, luego también tenemos que $\angle FBC=90-45-15-15=15$. En otras palabras, $FB$ es bisectriz (y por tanto mediatriz) en el triángulo isósceles $CBE$, luego también lo es del triángulo equilátero $EFC$. Esto nos lleva a que $\angle EFB=\angle BFE=30$. Si trazamos ahora el segmento $PF$, que es paralelo a $BC$ por la simetría, tenemos que $\angle PFB=\angle CBF=15$ por ser ángulos internos alternos, luego $\angle DFP=45+15=60$ como queríamos probar.
¿Es posible colorear los puntos del plano OXY de coordenadas enteras con tres colores de tal modo que cada color aparezca infinitas veces en infinitas rectas paralelas al eje OX y tres puntos cualesquiera, cada uno de distinto color, no estén alineados? Justificar la respuesta.
pistasolución 1info
Pista. Asigna colores según la paridad de las coordenadas del punto.
Solución. La respuesta es que sí es posible y para justificarlo daremos una forma de colorearlo. Dado un punto de coordenadas $(x,y)$,
- Lo pintamos de color A si las coordenadas $x,y$ tienen distinta paridad.
- Lo pintamos de color B si $x$ e $y$ son pares.
- Lo pintamos de color C si $x$ e $y$ son impares.
De esta manera, los colores A y B aparecen infinitas veces en las rectas de la forma $y=2k$ y los colores A y C aparecen infinitas veces en las rectas de la forma $y=2k+1$. Queda ver que cualquier recta $r$ contiene puntos de a lo sumo dos colores. Está claro que podemos suponer que la recta $r$ contiene al menos dos puntos de coordenadas enteras $P_1=(x_1,y_1)$ y $P_2=(x_2,y_2)$ y podemos suponer que no hay puntos de coordenadas enteras en el interior del segmento $P_1P_2$, luego el vector director $\vec{v}=(x_2-x_1,y_2-y_1)$ es tal que los puntos de $r$ de coordenadas enteras son los de la forma $P_1+n\vec{v}$ con $n\in\mathbb{Z}$. Distingamos varios casos:
- Si las dos coordenadas de $v$ son impares, entonces todos los puntos de $r$ son o bien todos de color A (cuando $x_1$ e $y_1$ tienen distinta paridad) o bien alternan entre colores B y C (cuando $x_1$ e $y_1$ tienen la misma paridad).
- Si la primera coordenada de $v$ es impar y la segunda par, entonces los puntos de $r$ o bien alternan entre colores A y B o entre colores A y C (dependiendo de la paridad de $y_1$). Análogamente ocurre cuando la primera coordenada de $v$ es par y la segunda impar.
- No puede ocurrir que las dos coordenadas de $v$ sean pares ya que en tal caso el punto medio $P_1+\frac{1}{2}\vec{v}$ también tendría coordenadas enteras y estaría en el interior del segmento $P_1P_2$.
Nota. Una dificultad de este problema es que la intuición parece decirnos que la coloración no puede existir ya que hay demasiadas rectas posibles. Sin embargo, si nos ponemos en que sí puede existir y pensamos en que en cada recta con al menos dos colores estos alternan, es fácil llegar a la solución propuesta.
Retos de la semana 44 de 2025
Se sabe que un dodecaedro regular es un poliedro regular con 12 caras pentagonales iguales y concurriendo 3 aristas en cada vértice. Se pide calcular, razonadamente,
- el número de vértices;
- el número de aristas;
- el número de diagonales de todas las caras;
- el número de segmentos rectilíneos determinados por cada dos vértices;
- el número de diagonales del dodecaedro.
pistasolución 1info
Pista. Razona con cuidado intentando no contar un mismo elemento varias veces.
Solución. Las caras son 12 polígonos que tienen 5 lados cada uno (un total de $12\cdot 5=60$ lados). En esta suma de lados tenemos cada arista contada por duplicado, lo que hace un total de $30$ aristas. Como tres de ellas concurren en cada vértice y cada arista une dos vértices, tendremos un total de $2\cdot\frac{30}{3}=20$ vértices.
Cada cara tiene 5 diagonales, lo que hace un total de $5\cdot 12=60$ diagonales de todas las caras.
Cada par de vértices determina un segmento, luego habrá $\binom{20}{2}=190$ segmentos determinados por cada dos vértices. Finalmente, el número de diagonales del dodecaedro será igual a este número de segmentos descontando las diagonales de las caras y las aristas del poliedro, es decir, $190-60-30=100$.
Nota. Podemos comprobar que se cumple la fórmula de Euler
\[C-A+V=2,\]
donde $C=12$, $A=30$ y $V=20$ son el número de caras, aristas y vértices, respectivamente.
¿Cuántos números de cuatro cifras (comprendidos entre $1000$ y $9999$) verifican que la suma de sus cifras es mayor o igual que su producto? ¿Para cuántos de ellos se verifica la igualdad?
pistasolución 1info
Pista. Demuestra que, si ninguno de los números es cero, entonces hay al menos dos que son iguales a uno.
Solución. Ordenamos los cuatro dígitos como $a\leq b\leq c\leq d$ (la forma de ordenarlos no afecta a la suma ni al producto) y supongamos que $a+b+c+d\geq abcd$. Si algunos de estos dígitos son cero, se tiene claramente la desigualdad estricta (ya que la suma de los dígitos no puede ser cero). Hay $9^4=6561$ números con los cuatro dígitos distintos de cero, luego $9000=6561=2439$ en los que alguno de los dígitos es cero.
Supongamos ahora que ningún dígito es cero. No puede ser $b\geq 2$ ya que en tal caso se tendría que $abcd\geq bcd\geq 4d\geq a+b+c+d$ y la igualdad no se alcanza pues tendría que ser $a=1$ (en la primera desigualdad) y $a=b=c=d$ (en la última), lo cual es incompatible con $b\geq 2$. Deducimos así que $a=b=1$, lo que nos deja con la desigualdad $2+c+d\geq cd$, que se escribe de forma equivalente como $(c-1)(d-1)\leq 3$.
- Si $c=1$, entonces $d$ puede ser cualquier número entre $1$ y $9$, lo que nos da la solución 1111 además todos los números que son permutación de $111d$. Esto nos da un total de $1+8\cdot 4=33$ soluciones en las cuales no se da nunca la igualdad.
- Si $c=2$, entonces $d$ puede ser 2, 3 o 4 y con el 4 se da la igualdad. Esto nos da 6 soluciones que son permutación de 1122, 12 soluciones que son permutación de 1123 y 12 soluciones que son permutación de 1124. Esto hace un total de 30 soluciones y solo en 12 de ellas se da la igualdad.
- Si $c\geq 3$ ya no hay ninguna solución pues tendría que ser $d\geq 3$.
Recapitulando, tenemos $2439+33+30=2502$ soluciones y solamente en $12$ de ellas se obtiene la igualdad.
Retos de la semana 43 de 2025
¿Cuál es el menor valor positivo posible de $36^m-5^n$, siendo $m$ y $n$ números naturales?
pistasolución 1info
Pista. ¿Cuáles pueden ser las cifras de las unidades del número $36^m-5^n$?
Solución. Observemos que la expresión decimal de $36^m$ siempre termina en $6$ mientras que la de $5^n$ siempre lo hace en $5$ luego $36^m-5^n$ siempre termina en $1$ independientemente de los valores de $m$ y $n$. Además, para $m=1$ y $n=2$, el resultado es $11$ luego si descartamos que pueda ocurrir $36^m-5^n=1$, habremos terminado y la respuesta será $11$.
Si ocurriera que $36^m-5^n=1$, entonces $(6^m-1)(6^m+1)=36^m-1=5^n$, de donde $6^m+1$ debería ser una potencia de $5$ pero, módulo $5$, este número es congruente con $2$ y hemos llegado a una contradicción.
Sean $x,y,z$ reales positivos tales que $x+y+z=3$. Hallar el valor máximo alcanzado por
\[\sqrt{x}+\sqrt{2y+2}+\sqrt{3z+6}.\]
¿Para qué valores de $x,y,z$ se alcanza dicho máximo?
pistasolución 1info
Pista. Utiliza la desigualdad de las medias con pesos, o la desigualdad de Jensen.
Solución. La desigualdad entre las medias aritmética y cuadrática con pesos nos dice que
\[au+bv+cw\leq\sqrt{a u^2+bv^2+cw^2},\]
donde $a,b,c,u,v,w$ son números reales positivos tales que $a+b+c=1$ (la forma usual de la desigualdad entre las medias aritmética y cuadrática se obtiene para los pesos $a=b=c=\frac{1}{3}$). Ahora aplicamos este resultado a los números $a=\frac{1}{6}$, $b=\frac{1}{3}$ y $c=\frac{1}{2}$ (que suman la unidad), $u=6\sqrt{x}$, $v=3\sqrt{2y+2}$ y $w=2\sqrt{3z+6}$. Sustituyendo estos valores tenemos que
\[\sqrt{x}+\sqrt{2y+2}+\sqrt{3z+6}\leq\sqrt{\frac{36x}{6}+\frac{9(2y+2)}{3}+\frac{4(3z+6)}{2}}=\sqrt{6(x+y+z)+18}.\]
Usando ahora que $x+y+z=3$ y simplificando, la desigualdad anterior queda
\[\sqrt{x}+\sqrt{2y+2}+\sqrt{3z+6}\leq 6.\]
Para ver que $6$ realmente es el máximo buscado y responder a la última pregunta del enunciado, vamos a ver que se alcanza la igualdad y en qué valores. La igualdad en la desigualdad de las medias con pesos se alcanza cuando los números son iguales, es decir, cuando $u=v=w$. Elevando al cuadrado, esto equivale a que $36x=18(y+1)=12(z+2)$. Teniendo en cuenta que $x+y+z=3$, es fácil despejar $x=y=z=1$. Como para $x=y=z=1$ se alcanza la igualdad, deducimos que sólo se alcanza para esta elección de las variables, terminando así la solución.
Nota. La desigualdad entre las medias aritmética y cuadrática con pesos es equivalente a la desigualdad de Jensen (con pesos) aplicada a la función convexa $f(x)=x^2$, lo que da lugar a otra forma de enfocar esta misma solución.
Retos de la semana 42 de 2025
Prueba que, para todo $a,b,c\gt 0$, se cumple que
\[\frac{a^2}{b^3c}-\frac{a}{b^2}\geq \frac{c}{b}-\frac{c^2}{a}.\]
¿En qué caso se cumple la igualdad?
pistasolución 1info
Pista. Factoriza la expresión $\frac{a^2}{b^3c}-\frac{a}{b^2}-\frac{c}{b}+\frac{c^2}{a}$ poniendo previamente denominador común.
Solución. Observemos que
\begin{align*}
\frac{a^2}{b^3c}-\frac{a}{b^2}-\frac{c}{b}+\frac{c^2}{a}&=\frac{a^3-a^2 b c-a b^2 c^2+b^3 c^3}{a b^3 c}\\
&=\frac{c^2}{a}\cdot\left(\frac{a^3}{b^3c^3}-\frac{a^2}{b^2c^2}-\frac{a}{bc}+1\right).
\end{align*}
Obtenemos así el polinomio $x^3-x^2-x+1$ tras el cambio $x=\frac{a}{bc}$. Este polinomio se puede factorizar como $(x-1)^2(x+1)$, luego podemos proseguir factorizando como
\begin{align*}
\frac{a^2}{b^3c}-\frac{a}{b^2}-\frac{c}{b}+\frac{c^2}{a}
&=\frac{c^2}{a}\cdot\left(\frac{a}{bc}-1\right)^2\left(\frac{a}{bc}+1\right)\geq 0.
\end{align*}
La igualdad se da cuando el factor $\frac{a}{bc}-1$ se anula (ya que el resto de factores son estrictamente positivos), es decir, cuando $a=bc$.
Problema 431
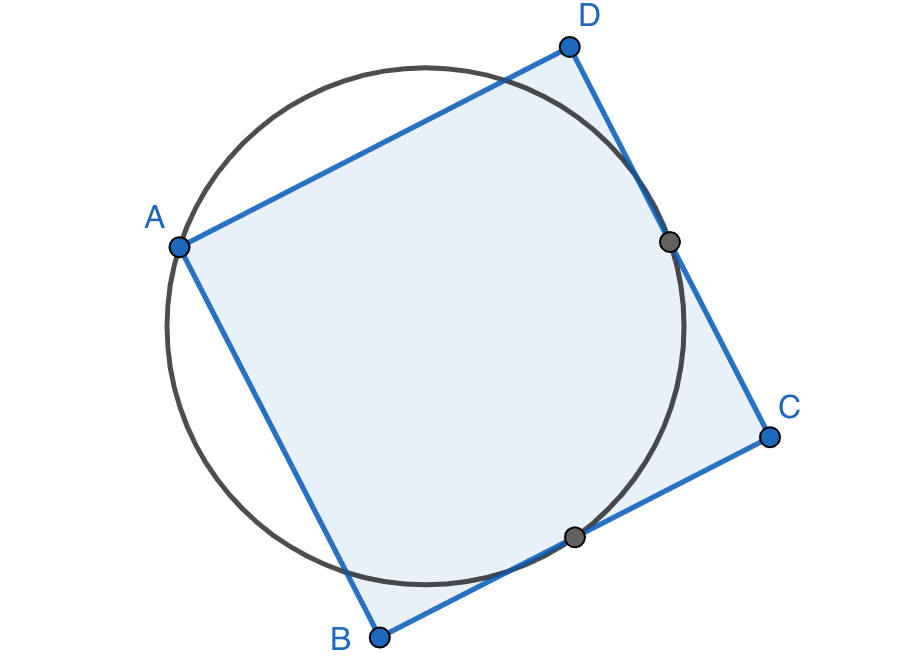
En un cuadrado $ABCD$ se traza una circunferencia que pasa por el vértice $A$ y por los puntos medios de los lados $BC$ y $CD$. Determinar si es mayor la longitud de la circunferencia o el perímetro del cuadrado.
pistasolución 1info
Pista. El teorema de Pitágoras puede ser útil.
Solución. Supongamos que el cuadrado tiene lado 1 sin perder generalidad. Sea $O$ el centro de la circunferencia y sean $M$ y $N$ los puntos medios de los lados $BC$ y $CD$. Llamando $P$ al punto medio de $MN$ y usando el teorema de Pitágoras se calcula fácilmente $AM=\frac{\sqrt{5}}{2}$ y $MP=\frac{1}{2}MN=\frac{\sqrt{2}}{4}$. Además, $AO=OM=R$, el radio de la circunferencia. Por lo tanto, el teorema de Pitágoras en los triángulos rectángulos $AMP$ y $OMP$ nos dice que
\[\frac{5}{4}=\frac{1}{8}+(R+OP)^2,\qquad R^2=OP^2+\frac{1}{8}.\]
Este sistema de dos ecuaciones con incógnitas $OP$ y $R$ se resuelve fácilmente, obteniendo como únicas soluciones positivas:
\[OP=\frac{\sqrt{2}}{3},\qquad R=\frac{5\sqrt{2}}{12}.\]
Por lo tanto, la longitud de la circunferencia es $2\pi R=\frac{5\sqrt{2}\pi}{6}$, mientras que el perímetro del cuadrado es $4$. Como $\pi^2\lt 10\lt \frac{576}{50}$, tomando raíces cuadradas obtenemos que $\frac{5\sqrt{2}\pi}{6}\lt 4$, es decir, la longitud de la circunferencia es menor que el perímetro del cuadrado.
Nota. El valor de $R$ también se deduce de la fórmula para el radio de la circunferencia circunscrita al triángulo $AMN$, es decir,
\[R=\frac{MN\cdot AM\cdot AN}{\sqrt{p(p-MN)(p-AM)(p-AN)}},\]
donde $p=\frac{1}{2}(AM+MN+AN)$ es el semiperímetro del triángulo.
Retos de la semana 41 de 2025
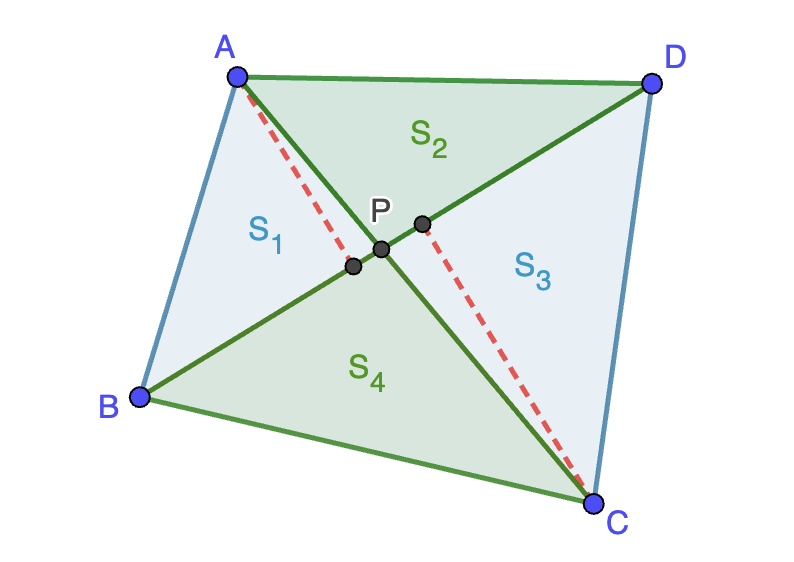
Un cuadrilátero convexo tiene la propiedad que cada una de sus dos diagonales
biseca su área. Demostrar que este cuadrilátero es un paralelogramo.
pistasolución 1info
Pista. Usa que el área es $\frac{1}{2}$ de la base por la altura en los cuatro triángulos en que las diagonales dividen al cuadrilátero.
Solución. Sea $ABCD$ el cuadrilátero convexo y $P$ el punto de corte de las diagonales. Si llamamos $S_1,S_2,S_3,S_4$ a las áreas de los cuatro triángulos en que las diagonales dividen al cuadrilátero, como se indica en la figura, entonces la propiedad de la bisección nos dice que
\[S_1+S_2=S_2+S_3=S_3+S_4=S_4+S_1\ \Longleftrightarrow\ \begin{cases}S_1=S_3,\\S_2=S_4.\end{cases}\]
Ahora bien, para que la diagonal $BD$ biseque, las distancias de $A$ y $C$ a la recta $BD$ deben ser las mismas (las alturas de los triángulos $ABD$ y $BCD$ de base común $BD$, indicadas con línea discontinua roja). Por lo tanto, tiene que ser $BP=DP$ para que se cumpla que $S_1=S_3$. Análogamente, se demuestra que $AP=CP$, luego hemos llegado a que las diagonales se cortan en su punto medio y esto implica que $ABCD$ es un paralelogramo.
Un grupo de $12$ piratas de edades diferentes se reparte $2022$ monedas,
de manera que cada pirata (salvo el más joven) tiene una moneda más que el siguiente más joven. A continuación, cada día se procede de la siguiente manera: se escoge a un pirata que tenga al menos $11$ monedas, y ese da una moneda a todos los demás. Encontrar el mayor número de monedas que un pirata puede llegar a tener.
pistasolución 1info
Pista. Trabaja con las monedas módulo $12$.
Solución. Observamos en primer lugar que el reparto es posible ya que la ecuación $a+(a+1)+(a+2)+\ldots+(a+11)=2022$ tiene solución entera $a=163$, de forma que los piratas obtienen desde $163$ monedas el menor hasta $163+11=174$ el mayor. Trabajando módulo $12$, a cada uno le toca un número de monedas con un resto distinto, pero la idea fundamental es que tras hacer un traspaso de monedas, cada uno se queda con $1$ moneda más (módulo $12$, cosa que no le hará gracia al que pierde $11\equiv -1$ monedas). Por tanto, a lo largo de todo el proceso, hemos encontrado el invariante de que todos los restos serán distintos. Esto nos dice que la configuración en que un pirata acumula el mayor número de monedas es que los otros tengan $0,1,2,3,\ldots,10$ monedas y él tenga las $1965$ restantes.
Todavía nos queda por ver que esto es posible, es decir, hemos buscado el que teóricamente es el mejor escenario posible, pero podría ocurrir que no se pudiera llegar a él. La idea para conseguirlo es que los once piratas menores repartan monedas mientras puedan y el mayor no reparta nada. En este proceso, por cada reparto de los menores, el mayor va acumulando una moneda más, luego los menores se van quedando (en conjunto) con una moneda menos en cada paso. De esta manera, el proceso debe terminar en el momento en que los once menores tienen todos ellos menos de $11$ monedas. Por el argumento de los restos módulo $12$, estos piratas deben tener necesariamente $0,1,2,\ldots,10$ monedas (en algún orden) y el mayor tendrá las $1965$ restantes.
Nota. El problema no tiene nada que ver con $12$ o $2022$ salvo que $2022$ es la suma de $12$ enteros consecutivos. Convéncete de que el mismo problema se resuelve de forma análoga para $m$ piratas y $a+\frac{m(m-1)}{2}$ monedas (para cualesquiera enteros $m\geq 2$ y $a\geq 0$).
Retos de la semana 40 de 2025
Se dan 98 puntos sobre una circunferencia. María y José juegan alternativamente de la siguiente forma: cada uno de ellos traza un segmento uniendo dos de los puntos que no hayan sido unidos entre sí anteriormente. El juego termina cuando los 98 puntos han sido usados como extremos de un segmento al menos una vez, siendo el vencedor quien dibuja el último trazo. Si José inicia el juego, ¿quién puede asegurarse la victoria?
Solución. Probaremos por inducción que José tiene una estrategia tal que, para todo $n\geq 0$, la primera vez que hay $4n+2$ puntos utilizados, José ha sido el último en jugar. Como $98$ es de la forma $4n+2$, esto nos dice que José tiene una estrategia ganadora.
El caso base de inducción es $n=0$, que se cumple ya que, coloque donde coloque José, habrá $4\cdot 0+2=2$ puntos utilizados y él ha sido el último en jugar. Supongamos entonces que después de jugar José, hay $4n+2$ puntos utilizados y demostremos que, después de cierto número de jugadas de ambos jugadores, habrá $4n+6$ puntos utilizados y José habrá sido el último en jugar. La forma de proceder de José después de cada jugada de María es la siguiente:
- Si después de la jugada de María sigue habiendo $4n+2$ puntos utilizados (María ha unido dos que ya habían sido utilizados), entonces José une uno ya utilizado con otro no utilizado previamente y ahora hay $4n+3$ utilizados.
- Si después de la jugada de María hay $4n+3$ puntos utilizados, entonces José une dos que ya hayan sido utilizados previamente y siguen quedando $4n+3$ utilizados.
- Si después de la jugada de María hay $4n+4$ puntos utilizados, entonces José une dos que ya no hayan sido utilizados hasta el momento, quedando utilizados $4n+6$.
- Si después de la jugada de María hay $4n+5$ puntos utilizados, entonces José une uno que no haya sido utilizados con otro que sí y quedan utilizados $4n+6$.
Está claro que José puede hacer siempre utilizar puntos no utilizados, luego sólo habrá que justificar que si después de la jugada de María hay $4n+3$ puntos utilizados, entonces quedan dos de ellos que no han sido unidos y José puede unirlos. El número de uniones posibles entre $4n+3$ puntos está dado por $(4n+3)(2n+1)$, que es un número impar. Como José siempre juega en los turnos impares, no puede ser María la que complete todas las uniones posibles entre los $4n+3$ puntos.
Finalmente, observemos que María en su turno nunca se le presentan $4n+4$ ni $4n+5$ puntos utilizados, luego no puede ser la primera en utilizar los $4n+6$ puntos, lo que demuestra que esta es la estrategia ganadora para José.
Nota. Este es un problema que admite muchas discusiones de casos y aproximaciones ligeramente distintas. La solución arriba presentada tiene la ventaja de que se puede adaptar para cualquier número de la forma $4n+2$ en lugar de $98$.
Sean $k$, $m$ y $n$ enteros positivos tales que $k+m+1$ es un primo estrictamente mayor que $n+1$. Si $C_s$ denota el entero $s(s+1)$, demostrar que el producto
\[(C_{m+1} − C_k)(C_{m+2}-C_k)\cdots(C_{m+n}-C_k)\]
es divisible por $C_1C_2\cdots C_n$.
pistasolución 1info
Pista. Observa en primer lugar que puedes factorizar $C_{m+i}-C_k=(m+k+i+1)(m-k+i)$ y expresa el producto del enunciado en términos de números combinatorios.
Solución. En primer lugar, vamos a desarrollar los factores que aparecen en ese producto para obtener una expresión más sencilla. Observamos que
\begin{align*}
C_{m+i}-C_k&=(m+i+1)(m+i)-(k+1)k\\
&=(m+i)^2-k^2+m+i-k\\
&=(m+k+i)(m-k+i)+m-k+i\\
&=(m+k+i+1)(m-k+i).
\end{align*}
Por lo tanto, podemos agrupar factores para expresar
\begin{align*}
&\frac{(C_{m+1}-C_k)\cdots(C_{m+n}-C_k)}{C_1C_2\cdots C_n}\\
&\quad=\frac{(m+k+2)(m-k+1)\cdots(m+k+n+1)(m-k+n)}{1\cdot 2\cdot 2\cdot 3\cdots n(n+1)}\\
&\quad=\frac{(m+k+2)\cdots(m+k+n+1)(m-k+1)\cdots(m-k+n)}{n!(n+1)!}\\
&\quad=\frac{1}{m+k+1}\binom{m+k+n+1}{n+1}\binom{m-k+n}{n}.
\end{align*}
Los números combinatorios son enteros pero falta por ver que alguno de ellos es divisible por el primo $m+k+1$. Claramente lo es el primero de ellos dado que en
\[\binom{m+k+n+1}{n+1}=\frac{(m+k+1)(m+k+2)\cdots(m+k+n+1)}{(n+1)!}\]
el numerador es múltiplo de $m+k+1$ y el denominador no lo es ya que $n+1\lt m+k+1$ por hipótesis.
Retos de la semana 39 de 2025
Demostrar que $m(m+1)$ no es la potencia de ningún número entero para ningún número natural $m\in\mathbb{N}$.
pistasolución 1info
Pista. Los números $m$ y $m+1$ son primos relativos.
Solución. Supongamos que $m(m+1)$ es igual a $a^n$ para $a,n\in\mathbb{N}$ con $n\geq 2$. Como $m$ y $m+1$ son primos relativos, tanto $m$ como $m+1$ deben ser potencias $n$-ésimas de enteros. No obstante, dos potencias $n$-ésimas se diferencia como mínimo en $2^n-1^n\geq 3$ para $n\geq 2$, mientras que $m$ y $m+1$ se diferencia solo en una unidad.
Hallar todas las ternas de reales positivos $(x,y,z)$ que cumplen el sistema
\[\left\{\begin{align*}
2x\sqrt{x+1}-y(y+1)=1,\\
2y\sqrt{y+1}-z(z+1)=1,\\
2z\sqrt{z+1}-x(x+1)=1.
\end{align*}\right.\]
pistasolución 1info
Pista. Observa que $(x^2+x+1)^2=(x^2-x-1)^2+4x^2(x+1)$.
Solución. La primera ecuación se puede escribir como $2x\sqrt{x+1}=1+y+y^2$ y, elevando al cuadrado, obtenemos $4x^2(x+1)=(1+y+y^2)^2$. Por lo tanto,
\[(x^2+x+1)^2=(x^2-x-1)^2+4x^2(x+1)=(x^2-x-1)^2+(y^2+y+1)^2,\]
por lo que se cumple la desigualdad
\[(x^2+x+1)^2\geq (y^2+y+1)^2\]
y la igualdad se da si y sólo si $x^2-x-1=0$. Razonando de forma similar con las otras ecuaciones, llegamos a que
\[(x^2+x+1)^2\geq (y^2+y+1)^2\geq (z^2+z+1)^2\geq (x^2+x+1)^2,\]
por lo que se ha de cumplir necesariamente la igualdad en todas las desigualdades y deducimos que $x=y=z=\frac{1+\sqrt{5}}{2}$, que es el único número positivo que cumple $x^2-x-1=0$.
Retos de la semana 38 de 2025
Sean $x$ e $y$ números reales entre $0$ y $1$. Probar que
\[x^3+xy^2+2xy\leq 2x^2y+x^2+x+y.\]
pistasolución 1info
Pista. Pasa todo al miembro de la derecha y manipula un poco completando algunos cuadrados perfectos.
Solución. Pasando todos los términos al segundo miembro podemos identificar algunos cuadrados perfectos y reescribir la desigualdad como
\[(1-x)(x-y)^2+y(1-y)+x\geq 0.\]
Esta desigualdad es evidente ya que $0\leq x,y\leq 1$.
Sea $ABCD$ un cuadrilátero convexo y $P$ un punto interior. Determinar qué
condiciones deben cumplir el cuadrilátero y el punto $P$ para que los cuatro
triángulos $PAB$, $PBC$, $PCD$ y $PDA$ tengan la misma área.
pistasolución 1info
Pista. Estas áreas se pueden calcular utilizando que el área de cada triángulo es $\frac{1}{2}$ del seno del ángulo en el vértice $P$ multiplicado por los dos lados que que tienen a $P$ como extremo.
Solución. Consideremos los ángulos $\alpha=\angle APB$, $\beta=\angle BPC$, $\gamma=\angle CPD$ y $\delta=\angle DPA$, que suman $360^\circ$. Entonces, podemos escribir
\begin{align*}
\text{Área}(PAB&)=\tfrac{1}{2}PA\cdot PB\cdot\mathrm{sen}(\alpha),&
\text{Área}(PCD&)=\tfrac{1}{2}PC\cdot PD\cdot\mathrm{sen}(\gamma),\\
\text{Área}(PBC&)=\tfrac{1}{2}PB\cdot PC\cdot\mathrm{sen}(\beta),&
\text{Área}(PDA&)=\tfrac{1}{2}PD\cdot PA\cdot\mathrm{sen}(\delta).
\end{align*}
En particular tenemos que $\text{Área}(PAB)\cdot\text{Área}(PCD)=\text{Área}(PBC)\cdot\text{Área}(PDA)$ ya que las cuatro áreas son iguales, lo que nos da la igualdad trigonométrica
\[\mathrm{sen}(\alpha)\mathrm{sen}(\gamma)=\mathrm{sen}(\beta)\mathrm{sen}(\delta).\qquad (\star)\]
Ahora bien, como $\alpha+\beta+\gamma+\delta=360^\circ$, la igualdad $(\star)$ nos dice que
\begin{align*}
\cos(\alpha+\gamma)=\cos(\beta+\delta)&\ \Leftrightarrow\ \cos(\alpha)\cos(\gamma)-\mathrm{sen}(\alpha)\mathrm{sen}(\gamma)=\cos(\beta)\cos(\delta)-\mathrm{sen}(\beta)\mathrm{sen}(\delta)\\
&\ \Leftrightarrow\ \cos(\alpha)\cos(\gamma)=\cos(\beta)\cos(\delta).
\end{align*}
Elevando esta última al cuadrado y cambiando $\cos^2=1-\mathrm{sen}^2$, llegamos a que
\[(1-\mathrm{sen}^2(\alpha))(1-\mathrm{sen}^2(\gamma))=(1-\mathrm{sen}^2(\beta))(1-\mathrm{sen}^2(\delta)).\]
Desarrollamos y usamos $(\star)$ de nuevo para obtener que
\[\mathrm{sen}^2(\alpha)+\mathrm{sen}^2(\gamma)=\mathrm{sen}^2(\beta)+\mathrm{sen}^2(\delta)\]
Sumando dos veces $(\star)$ a esta última ecuación, nos queda
\[\left(\mathrm{sen}(\alpha)+\mathrm{sen}(\gamma)\right)^2=\left(\mathrm{sen}(\beta)+\mathrm{sen}(\delta)\right)^2.\]
Como todos los senos son positivos (aquí usamos que el cuadrilátero es convexo, luego $\alpha,\beta,\gamma,\delta\lt 180^\circ$), deducimos finalmente que $\mathrm{sen}(\alpha)+\mathrm{sen}(\gamma)=\mathrm{sen}(\beta)+\mathrm{sen}(\delta)$. En otras palabras, las dos parejas $(\mathrm{sen}(\alpha),\mathrm{sen}(\gamma))$ y $(\mathrm{sen}(\beta),\mathrm{sen}(\delta))$ tienen la misma suma y el mismo producto, luego son iguales salvo reordenación.
- Si $\mathrm{sen}(\alpha)=\mathrm{sen}(\beta)$ y $\mathrm{sen}(\gamma)=\mathrm{sen}(\delta)$, hay dos posibilidades. La primera es que $\alpha+\beta=180^\circ$ o bien $\gamma+\delta=180^\circ$ (en cuyo caso, $P$ está en la diagonal $AC$). La segunda es que $\alpha=\beta$ y $\gamma=\delta$; como $\alpha+\beta+\gamma+\delta=360^\circ$, se tiene que $\alpha+\delta=180^\circ$ y $P$ está sobre $BD$.
- Si $\mathrm{sen}(\alpha)=\mathrm{sen}(\delta)$ y $\mathrm{sen}(\gamma)=\mathrm{sen}(\beta)$, se razona de forma totalmente análoga y $P$ estará sobre una de las dos diagonales.
Como $P$ está sobre una de las dos diagonales, supongamos que sobre $AC$, se sigue que $P$ es el punto medio de $AC$ ya que los triángulos $PAB$ y $PBC$ tienen bases $AP$ y $CP$ y la misma altura sobre ellas, luego $AP=CP$ para que sus áreas coincidan. Además, las distancias de $B$ y $D$ a $AC$ tienen que ser la misma para que los cuatro triángulos tengan la misma área.
En resumen, la condición que nos piden es que coincidan las distancias de dos vértices opuestos del cuadrilátero a la diagonal que pasa por los otros dos vértices y que el punto $P$ sea el punto medio de dicha diagonal.
Retos de la semana 37 de 2025
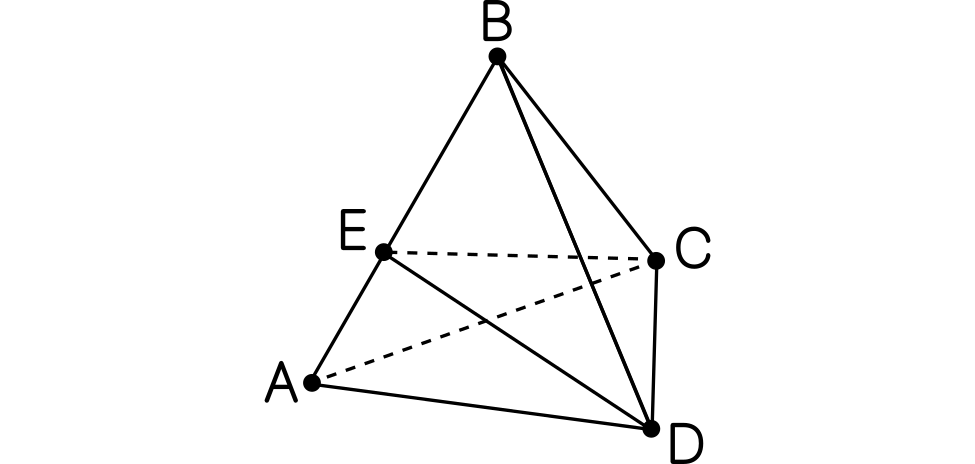
Se considera un tetraedro regular como el de la figura. Si el punto $E$ recorre la arista $AB$. ¿Cuándo el ángulo $\angle CED$ es máximo?
pistasolución 1info
Pista. Si $M$ es el punto medio de $CD$, demuestra el ángulo será máximo cuando la longitud de $EM$ sea mínima.
Solución. Sea $M$ el punto medio de $CD$, de forma que $EM$ es una altura del triángulo isósceles $CDE$. El ángulo $\alpha=\angle CED$ verifica que $\mathrm{tan}(\frac{\alpha}{2})=\frac{CM}{EM}$. El ángulo será máximo cuando la tangente sea máxima, es decir, cuando $EM$ sea mínimo ya que $CM$ no depende de dónde hayamos puesto el punto $E$. Ahora podemos restringirnos al plano que contiene al triángulo $ABM$. El segmento $EM$ está en este plano y su longitud será mínima cuando $EM$ sea perpendicular a $AB$, es decir, cuando $EM$ sea una altura de $ABM$, que coincide con la mediatriz por ser $ABM$ isósceles. Concluimos que el ángulo $\angle CED$ es máximo cuando $E$ es el punto medio de $AB$.
Nota. Usando el seno en lugar de la tangente, también puede razonarse de forma similar que lo que hay que minimizar es la longitud de $CE$, lo que nos lleva a que ha de ser perpendicular a $AC$ y $E$ tiene que ser el punto medio.
Consideramos una lista con los números $0$, $1$ y $\sqrt{3}$. De manera sucesiva, se va aplicando la siguiente operación: se escoge uno de los tres números de la lista y se le añade un múltiplo racional arbitrario de la diferencia de los otros dos. Repitiendo el proceso, ¿es posible conseguir que los tres números de la lista sean $0$, $\sqrt{3}-1$ y $\sqrt{3}+1$?
pistasolución 1info
Pista. Piensa en cada número $x+y\sqrt{3}$ como en el punto del plano de coordenadas $(x,y)$ y ahora piensa en en la operación propuesta como una operación sobre el triángulo que tiene a dichos números por vértices.
Solución. Los números que se obtienen de esta manera son siempre de la forma $x+y\sqrt{3}$ para ciertos $x,y\in\mathbb{Q}$. Vamos a identificar entonces cada número con el punto $(x,y)$ en el plano. Al sumarle a un punto un múltiplo racional de la diferencia de los otros dos, no hacemos más que mover uno de los vértices del triángulo que forman en la dirección paralela al lado opuesto (ya que la diferencia representa el vector director de la recta que forman dichos puntos en el plano). Originalmente, los tres puntos son $(0,0),(1,0),(0,1)$, que forman un triángulo de área $\frac{1}{2}$ y queremos llegar a los puntos $(0,0),(-1,1),(1,1)$, que forman un triángulo de área $1$. Por tanto, es imposible conseguir esos tres números.
Retos de la semana 36 de 2025
En cada uno de los vértices de un cubo hay una mosca. Al sonar un silbato, cada una de las moscas vuela a alguno de los vértices del cubo situado en una misma cara que el vértice de donde partió, pero diagonalmente opuesto a este. Al sonar el silbato, ¿de cuántas maneras pueden volar las moscas de modo que en ningún vértice queden dos o más moscas?
pistasolución 1info
Pista. Fíjate en que hay dos subconjuntos de cuatro moscas que se mueven independientemente de lo que haga el otro subconjunto.
Solución. Coloreamos los vértices del cubo de blanco y negro de forma que dos vértices adyacentes tengan colores distintos. Esto hace que los vértices diagonalmente opuestos de una misma cara tengan el mismo color y que haya 4 vértices blancos y 4 vértices negros. Ahora bien, una mosca puede ir desde cualquier vértice blanco a cualquier otro vértice blanco cada vez que toca el silbato, por lo que las moscas situadas en los vértices blancos tendrán tantos movimientos posibles como las permutaciones de cuatro elementos que no dejan ningún elemento fijo. Llamamos 1,2,3,4 a los vértices blancos. Si el vértice 1 va al vértice 2, entonces hay tres posibilidades para el vértice 2:
- Si el 2 vuelve al 1, entonces el 3 debe ir al 4 y el 4 al 3 para no dejar ningún vértice fijo y que no acaben dos moscas en el mismo vértice.
- Si el 2 va al 3, entonces el 3 debe ir al 4 (si fuera volviera al 1, entonces el 4 se quedaría fijo), luego el 4 debe volver al 1.
- Si el 2 va al 4, entonces el 4 debe ir al 3 y el 3 volver al 1 por el mismo razonamiento que en el punto anterior.
Por tanto, hay 3 posibilidades si el vértice 1 va al vértice 2. De la misma forma, hay 3 posibilidades si el 1 va al 3 y 3 posibilidades si el 1 va al 4, lo que nos da un total de 9 permutaciones de los vértices blancos. Como a los negros les pasa lo mismo, tendremos un total de $9\cdot 9=81$ formas en que pueden volar las moscas.
Nota. En el lenguaje de permutaciones, estamos diciendo que de las 24 permutaciones de 4 elementos, hay 3 productos de dos transposiciones y 6 ciclos de longitud 4, que son las 9 que no fijan ningún elemento.
Consideremos la sucesión de enteros positivos $\{x_n\}$ definida por $x_1=2$ y $x_{n+1}=2x_n^3+x_n$ para todo $n\geq 1$. Hallar la mayor potencia de $5$ que divide a $x_{2014}^2+1$.
pistasolución 1info
Pista. Demuestra por inducción que $x_n$ es múltiplo de $5^n$ pero no de $5^{n+1}$.
Solución. Se pueden calcular algunos términos, pero rápidamente el resultado se dispara ya que la sucesión crece exponencialmente:\[x_1^2+1=5,\quad x_2^2+1=325,\quad x_3^2+1=136469125,\ldots\] Vamos a probar por inducción sobre $n$ que $x_n^2+1$ es múltiplo de $5^n$ pero no de $5^{n+1}$. Si probamos esto, tendremos que la solución al problema es $5^{2024}$. Está claro que el caso $n=1$ es cierto ya que $x_1^2+1=5$ es múltiplo de $5$ pero no de $25$. También es cierto si $n=2$ ya que $x_2^2+1=325$ es múltiplo de $25$ pero no de $125$. Supongamos que la propiedad es cierta para $n\geq 2$, lo que nos permite escribir $x_n^2+1=5^ny_n$, siendo $y_n$ no múltiplo de $5$. Entonces, para $x_{n+1}$ podemos desarrollar y simplificar \begin{align*}x_{n+1}^2+1&=(2x_n^3+x_n)^2+1=(4x_n^4+4x_n^2+1)x_n^2+1\\\\&=(4(5^ny_n-1)^2+4(5^ny_n-1)+1)(5^ny_n-1)+1\\\\&=4\cdot 5^{3n}y_n^3-8\cdot 5^{2n}y_n^2+5^{n+1}y_n\\\\&=5^{n+1}(4\cdot 5^{2n-1}y_n^3-8\cdot 5^{n-1}y_n^2+y_n).\end{align*}Este número es múltiplo de $5^{n+1}$ pero no de $5^{n+2}$ ya que el factor $4\cdot 5^{2n-1}y_n^3-8\cdot 5^{n-1}y_n^2+y_n$ es congruente con $y_n$ módulo $5$. Aquí estamos usando que $n\geq 2$ para asegurar que $5^{n-1}$ es múltiplo de $5$, es decir, en la inducción hemos tenido que comprobar dos casos iniciales.
Retos de la semana 35 de 2025
Juan escribe la lista de parejas $(n,3^n)$ para $n=1,2,3,\ldots$ en una pizarra. A medida que va escribiendo la lista, subraya las parejas $(n,3^n)$ siempre que $n$ y $3^n$ tienen la misma cifra de las unidades. De las parejas subrayadas, ¿cuál ocupa la posición 2013?
Pista. La cifra de las unidades de $3^n$ se repite periódicamente conforme $n$ avanza en los números naturales.
Deslizamos un cuadrado de $10\text{cm}$ de lado por el plano $OXY$ de forma que los vértices de uno de sus lados estén siempre en contacto con los ejes de coordenadas, uno con el eje $OX$ y otro con el eje $OY$. Determina los lugares geométricos que en ese movimiento describen:
- El punto medio del lado de contacto con los ejes.
- El centro del cuadrado.
- Los vértices del lado de contacto y del opuesto en el primer cuadrante.
pistasolución 1info
Pista. Utiliza coordenadas. En algún momento vas a tener que saber reconocer por su ecuación una cónica cuyos ejes no son paralelos a los ejes de coordenadas.
Solución. Por la simetría del problema, podemos pensar en que los puntos de contacto con los ejes están en el semiplano superior y luego añadir la configuración simétrica respecto del origen para completar los lugares geométricos que nos piden. Supondremos entonces que los vértices de contacto tienen coordenadas $A=(a,0)$ y $B=(0,\sqrt{100-a^2})$ y que, por tanto, $a$ se mueve en el intervalo $(-10,10)$. Observemos que $a=-10$ se corresponde con el cuadrado apoyado en el semieje negativo $OX$ y que el cuadrado está contenido en el tercer cuadrante, mientras que si $a=10$ entonces el cuadrado estará contenido completamente en el primer cuadrante.
- El punto medio $M$ del lado $AB$ tiene coordenadas $x_M=\tfrac{a}{2}$ e $y_M=\tfrac{1}{2}\sqrt{100-a^2})$, luego se cumple que $x_M^2+y_M^2=25$. Esto nos dice que $M$ describe la mitad superior de la circunferencia de radio $5$ y centro $(0,0)$. Por simetría, $M$ describe la circunferencia entera cuando dejamos que $B$ también se mueva por el semiplano inferior.
- Un vector normal al lado de contacto es $\vec{n}=(\sqrt{100-a^2},a)$ y tiene módulo $10$ igual a la longitud del lado. El centro del cuadrado puede calcularse como $C=M+\frac{1}{2}\vec{n}$, que tiene coordenadas $x_C=\tfrac{a}{2}+\frac{1}{2}\sqrt{100-a^2}$ e $y_C=\tfrac{1}{2}\sqrt{100-a^2})+\frac{a}{2}$, por lo que se cumple que $x_C=y_C$. Queda por ver qué puntos exactamente de la recta $x=y$ (bisectriz del primer cuadrante) toma el punto $C$, para lo que consideramos la función $f(a)=\tfrac{a}{2}+\frac{1}{2}\sqrt{100-a^2}$, que es continua en $[-10,10]$ y derivable en $(-10,10)$. Se verifica que $f'(a)=\frac{1}{2}-\frac{x}{2\sqrt{100-x^2}}$, de donde es fácil ver que $f'(a)=0$ tiene por única solución $a=5\sqrt{2}$, donde la función alcanza su máximo absoluto en el intervalo $[-10,10]$ y el valor máximo correspondiente es $f(5\sqrt{2})=5\sqrt{2}$. El mínimo absoluto se alcanza en el extremo $a=-10$, donde no es derivable, pero se cumple que $f(-10)=-5$. De esta forma, $C$ toma todos los valores en el segmento que une $(-5,-5)$ y $(5\sqrt{2},5\sqrt{2})$. Al considerar también el caso simétrico en que $B$ recorre el semiplano inferior, concluimos que el lugar geométrico de $C$ es el segmento rectilíneo que une $(-5\sqrt{2},-5\sqrt{2})$ y $(5\sqrt{2},5\sqrt{2})$ contenido en la bisectriz del primer cuadrante, incluyendo los extremos de dicho segmento.
- Un vértice $V$ opuesto al lado $AB$ viene dado por $V=A+\vec{n}$, luego tiene coordenadas $x_V=a+\sqrt{100-a^2}$ e $y_V=a$. Tenemos así que $(x_V-y_V)^2=100-y_V^2$ o equivalentemente $x_V^2-2x_Vy_V+2y_V^2=100$. Se trata, por tanto, de saber qué conjunto representa la ecuación $x^2-2xy+2y^2=100$. Como es un polinomio cuadrático, deducimos que se trata de una cónica; como podemos completar cuadrados para expresarlo como $(x-y)^2+y^2=100$ y ambos cuadrados tienen coeficientes positivos, deducimos que se trata de una elipse; como no tiene términos lineales en $x$ o $y$, deducimos que está centrada en el origen, aunque no tiene sus ejes paralelos a los ejes de coordenadas por tener término en $xy$. Ahora bien, al variar $a$ en $[-10,10]$ se ve fácilmente que se recorren todos los puntos de la elipse una vez se ha añadido el caso en que $B$ recorre el semieje $OY$ negativo.
Nota. Hemos supuesto que cuando $A$ y $B$ están en los semiejes positivos, el cuadrado está enteramente contenido en el primer cuadrante. Existe otra posibilidad que es suponer que en ese caso el cuadrado mira hacia el otro lado. No obstante, en tal caso, los lugares geométricos que nos piden serían simétricos de los obtenidos ya que se trataría simplemente de girar $90^\circ$ la figura.
Retos de la semana 34 de 2025
Sean $a$, $b$ y $c$ tres números reales positivos cuyo producto es $1$. Demostrar que si la suma de estos números es mayor que la suma de sus recíprocos, entonces exactamente uno de ellos es mayor que $1$.
pistasolución 1info
Pista. Utiliza las condiciones dadas para probar que $(a-1)(b-1)(c-1)\gt 0$.
Solución. Usando que $abc=1$ y la hipótesis de que la suma de los números es mayor que la de la suma de sus recíprocos (inversos multiplicativos), podemos escribir
\begin{align*}
0&\lt a+b+c-\frac{1}{a}-\frac{1}{b}-\frac{1}{c}=a+b+\frac{1}{ab}-\frac{1}{a}-\frac{1}{b}-ab\\
&=\frac{a^2b+ab^2+1-b-a-a^2b^2}{ab}=\frac{(a-1)(b-1)(1-ab)}{ab}\\
&=(a-1)(b-1)(\tfrac{1}{ab}-1)=(a-1)(b-1)(c-1).
\end{align*}
Esta desigualdad estricta nos dice que ninguno de los números puede ser igual a $1$. Para que el producto de los signos en $(a-1)(b-1)(c-1)$ sea positivo, exactamente uno de los tres números debe ser mayor que $1$ (si los tres números son mayores que $1$, entonces el producto también sería positivo pero tendríamos $abc\gt 1$, en contra de lo que nos dice el enunciado).
En el interior de una circunferencia de centro $O$ y radio $r$, se toman dos puntos $A$ y $B$ simétricos respecto de $O$. Se considera $P$ un punto variable sobre esta circunferencia y se traza la cuerda $PP'$ perpendicular a $AP$. Sea $C$ el punto simétrico de $B$ respecto de $PP'$. Hallar el lugar geométrico del punto $Q$, interseccion de $PP'$ con $AC$ al variar $P$ sobre la circunferencia.
pistasolución 1info
Pista. Demuestra que $AQ+BQ$ es constante cuando se mueve $P$.
Solución. Consideremos los puntos $S$ y $S'$ simétricos de $P$ y $P'$ respecto del centro de la circunferencia, lo que define un rectángulo inscrito $PP'SS'$. Además, como $AP'$ es perpendicular a $PP'$, se tiene que $A$ pertenece al interior del segmento $PS'$ y $B$, por simetría, pertenece al segmento $SP'$. Por la simetría respecto de $O$ y la simetría de $B$ y $C$ respecto de $PP'$, s e tiene que $AS'=BP'=P'C$. Como los segmentos $AS'$ y $P'C$ son paralelos (están en lados opuestos del rectángulo), se tiene que $AS'P'C$ es un paralelogramo, luego $AC=P'S'=2r$. Finalmente, observamos que $QC=QB$ por simetría, luego $AQ+QB=AQ+QC=2r$ y deducimos que la suma de las distancias de $Q$ a $A$ y $B$ es constante. Esto nos asegura que $Q$ está en una elipse de focos $A$ y $B$.
Nos queda determinar de qué elipse se trata concretamente ya que hay infinitas con focos $A$ y $B$. Si prolongamos $AB$ hasta que corte en un punto $X$ a la circunferencia, se tiene claramente que $AX+XB=2r$, luego $X$ también está en la misma elipse. Como la elipse es simétrica respecto de la recta $AB$, no queda otra que ser tangente a la circunferencia en $X$. Además, como $Q$ pertenece a la cuerda $PP'$, los puntos de la elipse siempre son interiores a la circunferencia. Concluimos que el lugar geométrico es la única elipse de focos $A$ y $B$ tangente interiormente a la circunferencia.
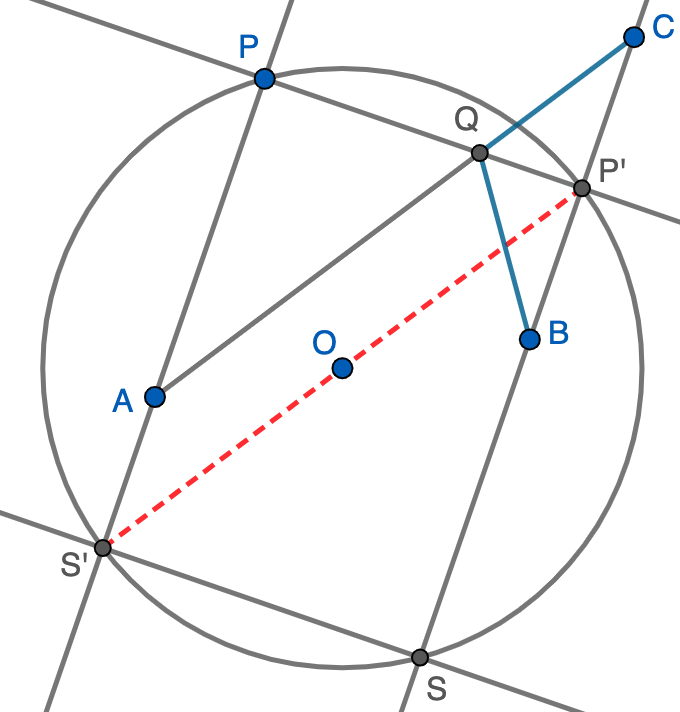
Retos de la semana 33 de 2025
Sea $ABC$ un triángulo rectángulo en $C$ no isósceles con catetos $b\gt a$.
- Hallar el lado del cuadrado $AXYZ$ que circunscribe al triángulo $ABC$ (los vértices $B$ y $C$ tienen que estar en lados distintos del cuadrado).
- Explicar paso a paso cómo construir el cuadrado $AXYZ$ con regla y compás.
pistasolución 1info
Pista. Observa que $ACZ$ y $BCY$ son triángulos semejantes.
Solución. En la figura hemos representado el triángulo $ABC$ inscrito en el cuadrado $AXYZ$. Como el triángulo es rectángulo en $C$, se tiene que $\angle YBC=90^\circ-\angle YCB=\angle ACZ$, luego los triángulos $BCY$ y $ACZ$ son semejantes. Si llamamos $\ell$ al lado del cuadrado, tendremos que $CZ=\sqrt{b^2-\ell^2}$ y $CY=\ell-CX$, luego la semejanza nos dice que
\begin{align*}
\frac{CY}{AZ}=\frac{BC}{AC}&\ \Leftrightarrow\ \frac{\ell-\sqrt{b^2-\ell^2}}{\ell}=\frac{a}{b}\ \Leftrightarrow\ 1-\sqrt{\frac{b^2}{\ell^2}-1}=\frac{a}{b}\\
&\ \Leftrightarrow\ \sqrt{\frac{b^2}{\ell^2}-1}=1-\frac{a}{b}\ \Leftrightarrow\ \frac{b^2}{\ell^2}=1+\left(1-\frac{a}{b}\right)^2\\
&\ \Leftrightarrow\ \frac{1}{\ell^2}=\frac{b^2+(b-a)^2}{b^4}\ \Leftrightarrow\ \ell=\frac{b^2}{\sqrt{2b^2-2ab+a^2}}.
\end{align*}
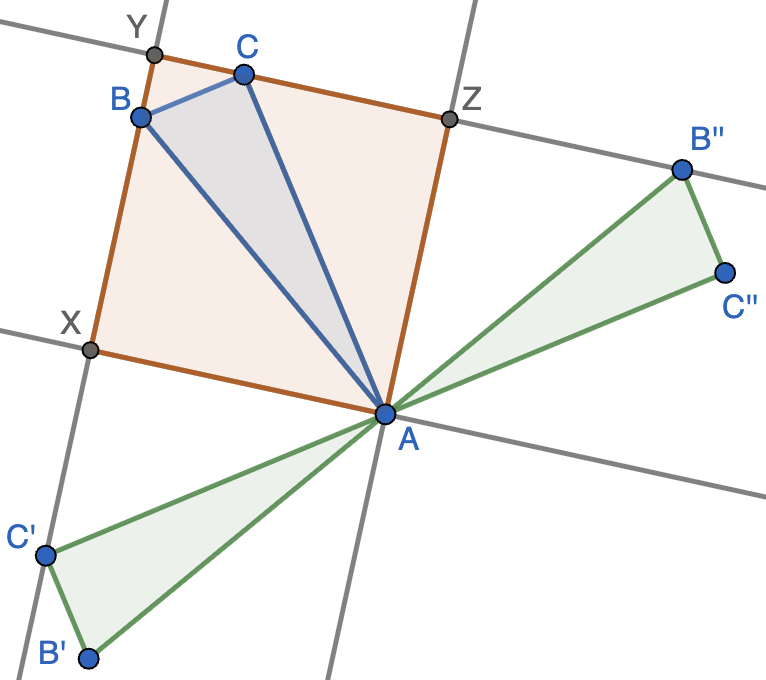
Para construir el cuadrado observamos que al rotar el triángulo $90^\circ$ en sentido horario y antihorario (como se muestra en la figura) con centro en $A$, obtenemos triángulos congruentes $AB'C'$ y $AB''C''$. El cuadrado $AXYZ$ se convierte en sendos cuadrados con un lado en común con él, luego las rectas $BC'$ y $CB''$ contienen a los lados del cuadrado. Ahora basta tomar $Y$ como su intersección y $X$ y $Z$ como los pies de las perpendiculares desde $A$.
Tenemos $42$ números naturales distintos colocados en fila. Entre cada dos consecutivos se escribe un signo de suma o de multiplicación y además se pueden añadir tantos paréntesis como sea necesario sin alterar el orden de los números. Demostrar que se puede conseguir de este modo que el resultado de la operación sea múltiplo de $750141$.
pistasolución 1info
Pista. Coloca paréntesis formando grupos de 3 y 7 números consecutivos en la fila. Demuestra que puedes colocar las operaciones dentro de cada paréntesis para que los grupos de 3 den un múltiplo de 3 y los grupos de 7 un múltiplo de 7.
Solución. Observemos que $750141=3^7\cdot 7^3$, luego vamos a dividir los $42$ números en $7$ grupos de $3$ y $3$ grupos de $7$. Cada grupo se pone entre paréntesis y luego se añade un signo de multiplicación entre paréntesis consecutivos. De esta forma, el problema se reduce a ver que en cada grupo de $3$ podemos conseguir un múltiplo de $3$ y en cada grupo de $7 un múltiplo de $7$.
- Grupos de 3. Si uno de los tres números es múltiplo de tres, simplemente multiplicamos los tres números. Si los tres números tienen todos resto 1 o todos resto 2 al dividirlos entre tres, sumamos los tres números. Si hay números con resto 1 y números con resto 2 mezclados, simplemente sumamos uno de cada consecutivos, los ponemos entre paréntesis y multiplicamos por el tercero.
- Grupos de 7. Aquí la distinción de casos se vuelve más tediosa (aunque se puede hacer), luego demostraremos de otra forma que hay una cadena consecutiva que suman un múltiplo de 7; bastará sumarla, ponerla entre paréntesis y multiplicar por el resto de números de este grupo. Pongamos que los números son $a_1,a_2,\ldots,a_7$ y vamos haciendo las sumas
\begin{align*}&a_1,\\&a_1+a_2,\\ &a_1+a_2+a_3,\\ &\vdots\\ &a_1+a_2+a_3+a_4+a_5+a_6+a_7.\end{align*}
Si una de ellas es múltiplo de $7$ habremos terminado; si no, todas dejarán resto entre $1$ y $6$ al dividirlas por $7$. Por el principio del palomar, algún resto se repetirá, luego basta restar la suma de más términos de la suma de menos términos para obtener una subsuma de la forma $a_k+a_{k+1}+\ldots+a_j$ múltiplo de $7$. Por ejemplo, si $a_1+a_2+a_3+a_4+a_5$ y $a_1+a_2$ dejan el mismo resto al dividir por $7$, entonces $a_3+a_4+a_5$ es múltiplo de $7$.
Nota. De la misma forma, se puede probar que en una lista de $n$ números enteros, existe alguna suma de números consecutivos que es múltiplo de $n$.
Retos de la semana 32 de 2025
Consideramos la siguiente figura formada por 12 vértices y 16 segmentos. ¿Es posible dibujar una curva que atraviese cada segmento una única vez sin pasar por ningún vértice?
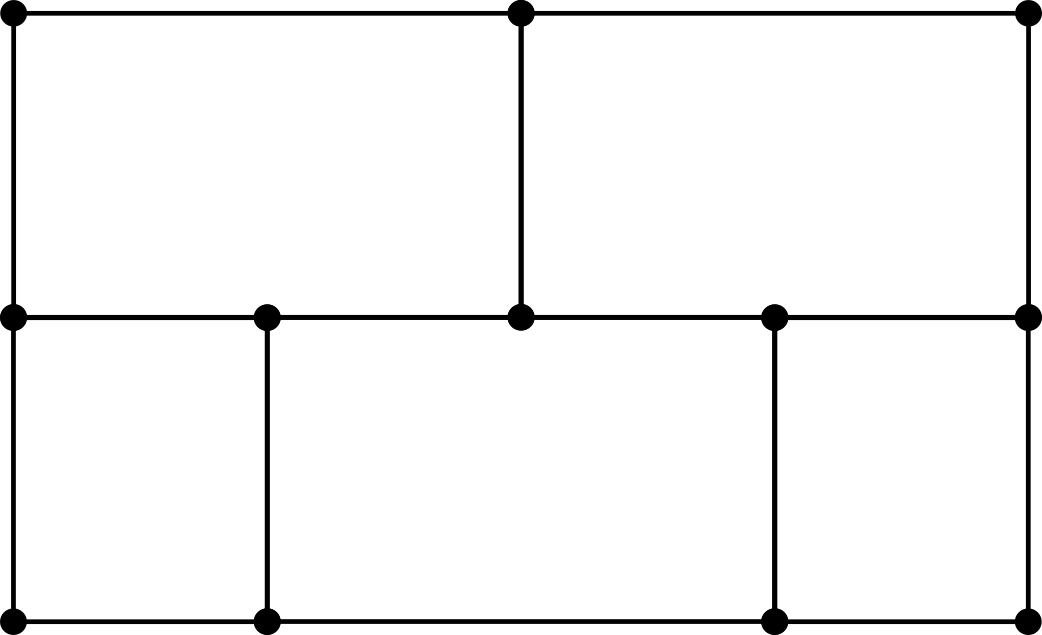
pistasolución 1solución 2info
Pista. ¿Qué pasa con la curva en las regiones con un número impar de lados?
Solución. Observemos que en la figura se forman tres pentagonos y dos cuadrados. Evidentemente, nuestra curva tendría que empezar fuera de (al menos) dos de los pentágonos. Cada vez que la curva atraviesa un lado de uno de estos pentágonos pasará de estar en el interior a estar en el exterior o del exterior al interior. Por tanto, como cada pentágono tiene un número impar de lados, la curva debería terminar en el interior de dos de los pentágonos, lo cual es absurdo. Concluimos que no existe dicha curva.
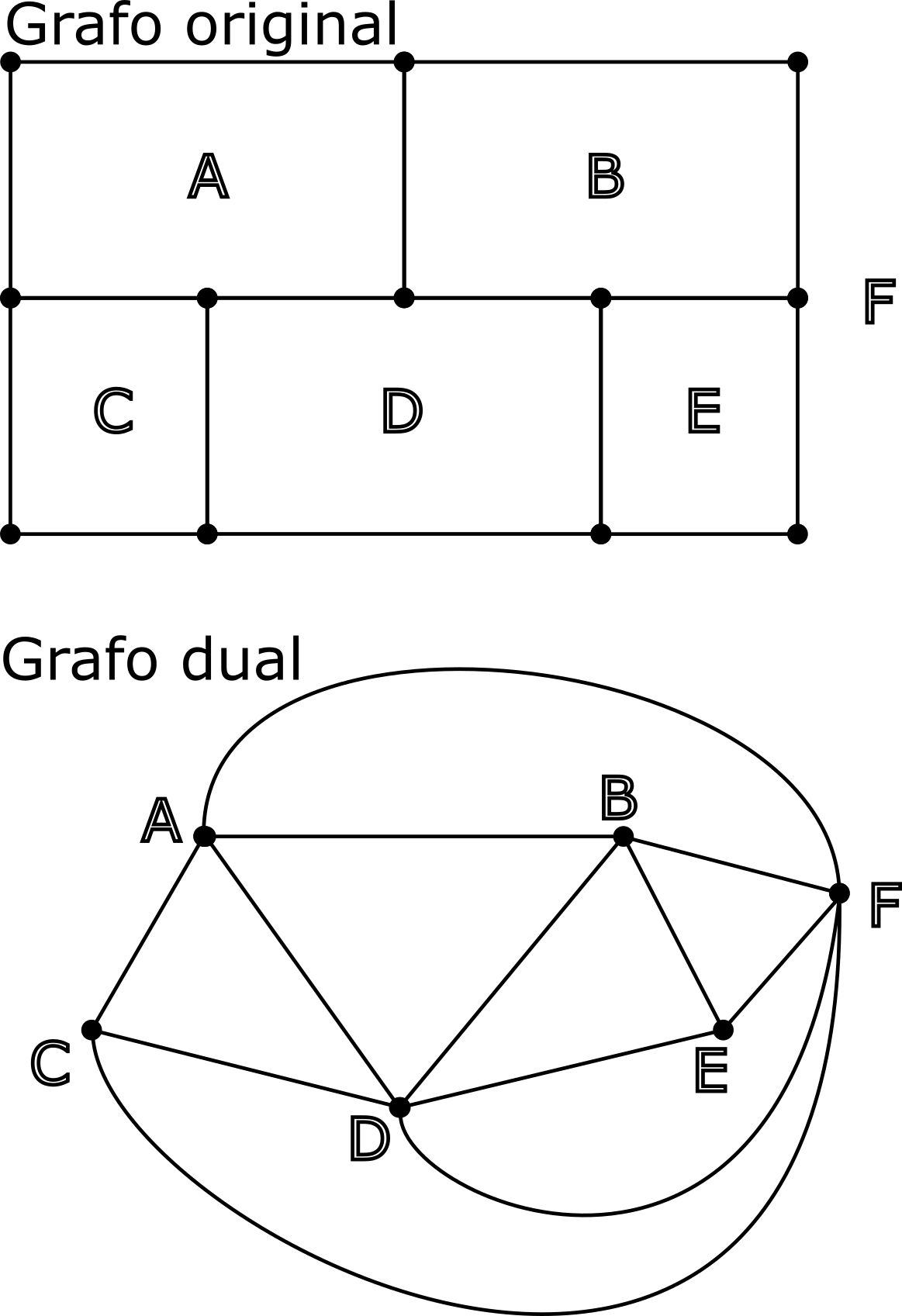
Solución. Esta es una solución muy estándar usando algo de teoría de grafos. La figura del enunciado es un grafo plano y podemos considerar el grafo dual, que tiene un vértice por cada cara del grafo original y en el que dos vértices se unen por una arista cuando representan a caras adyacentes (ver figura).
Atravesar una arista del grafo original equivale a recorrer una arista del grafo dual, por lo que el problema se reduce a encontrar un camino que pase por todas las aristas del grafo dual una sola vez. Esto no puede hacerse ya que eso implicaría que hay como máximo dos vértices del grafo dual a los que llegan un número par de aristas (Teorema de Euler). Sin embargo, el grafo dual tiene 4 vértices (C, D, E y F) a los que llegan un número par de aristas, por lo que concluimos que la curva buscada no puede existir.
Probar que para todo entero positivo $n$, la expresión decimal de
\[\frac{1}{n}+\frac{1}{n+1}+\frac{1}{n+2}\]
es un número decimal periódico mixto.
pistasolución 1info
Pista. Un número racional es periódico puro si y sólo si se puede expresar como $\frac{r}{s}$ y $s$ es un número natural que se escribe solo con dígitos $9$. Un número racional es limitado si se puede expresar como $\frac{r}{s}$ y $s$ solo tiene factores $2$ y $5$. Descarta ambas posibilidades y tendrás el problema resuelto.
Solución. Podemos poner denominador común y escribir
\[\frac{1}{n+1}+\frac{1}{n+2}+\frac{1}{n}=\frac{3 n^2+6 n+2}{n (n+1) (n+2)}.\]
Observamos que si $n$ es impar, entonces el numerador es impar y el denominador es par. Si $n=2k$ es par, entonces el denominador es múltiplo de $4$ ya que $n$ y $n+2$ son pares consecutivos, mientras que el numerador es igual a $2(6 k^2+6 k+1)$ y sólo tiene un factor $2$. Esto nos dice que en cualquier expresión como fracción del número $\frac{1}{n+1}+\frac{1}{n+2}+\frac{1}{n}$ tendremos que el denominador es par. En particular, nunca se puede poner como una fracción en la que el denominador sea $999\cdots 9$ (como les pasa a todos los periódicos puros).
Finalmente, descartamos también que el número sea un decimal exacto. Esto viene de que el denominador $n (n+1) (n+2)$ es múltiplo de $3$ (es el producto de tres enteros consecutivos) mientras que el numerador $3n^2+6n+2$ deja resto $2$ al dividirlo entre $3$. Un número decimal limitado se tiene que poder escribir como una fracción en la que el denominador sólo tiene factores $2$ o $5$, pero este argumento nos dice que en cualquier fracción que exprese a este número habrá un factor $3$ en el denominador.
Retos de la semana 31 de 2025
Encontrar todas las soluciones de la ecuación
\[nm = k(n + m)\]
donde $n$ y $m$ son números enteros y $k$ es un número primo mayor o igual que 2.
pistasolución 1info
Pista. Factoriza la ecuación como $(n-k)(n-k)=k^2$.
Solución. Observemos que la ecuación se puede escribir como
\[(m-k)(n-k)=k^2.\]
Si suponemos que $m\leq n$, como los divisores de $k^2$ son $\pm 1$, $\pm k$ y $\pm k^2$, tendrá que darse alguna de las siguientes posibilidades:
- $m-k=-k^2$, $n-k=-1$, de donde $m=k-k^2$ e $n=k-1$,
- $m-k=-k$, $n-k=-k$, de donde $m=n=0$,
- $m-k=1$, $n-k=k^2$, de donde $m=k+1$ e $n=k^2+k$,
- $m-k=k$, $n-k=k$, de donde $m=n=2k$.
Esto nos da la siguientes seis posibilidades para el par $(m,n)$:
\begin{align*}
&(k-k^2,k-1),&&(k-1,k-k^2),&&(0,0),&\\
&(k+1,k^2+k),&&(k^2+k,k+1),&&(2k,2k).&
\end{align*}
Nota. Este fue el problema 4 de la fase nacional de la Olimpiada Matemática Española de 1995.
Determinar los números reales $x\gt 1$ para los cuales existe un triángulo cuyos lados tienen longitudes
\[x^4+x^3+2x^2+x+1,\qquad 2x^3+x^2+2x+1,\qquad x^4-1.\]
pistasolución 1info
Pista. Determina cuál es el lado mayor y fíjate en que no debe alcanzar a la suma de los otros dos para que exista el triángulo (desigualdad triangular).
Solución. En primer lugar, vamos a determinar cuál es el lado mayor. Por un lado,
\[x^4+x^3+2x^2+x+1\gt x^4+1\gt x^4-1,\]
ya que $x$ es positivo. Usando que $x\gt 1$, tenemos que $x^4\geq x^3$ y $x^2\gt x$, luego
\[x^4+x^3+2x^2+x+1\gt x^3+x^3+x^2+x+x+1=2x^3+x^2+2x+1.\]
Sabiendo entonces que el primer lado es el mayor, tendremos que ver cuándo no supera a la suma de los otros dos, es decir, la respuesta al enunciado serán los números $x\gt 1$ tales que
\[x^4+x^3+2x^2+x+1\lt (2x^3+x^2+2x+1)+(x^4-1).\]
Tras simplificar y factorizar, nos queda $-x^3+x^2-x+1\lt 0$ y podemos factorizar el miembro de la izquierda para llegar a la desgualdad $(x^2+1)(1-x)\lt 0$, desigualdad que no se cumple para todo $x\gt 1$. Por tanto, para todo $x\gt 1$ hay un triángulo cuyos lados tienen las longitudes del enunciado.
Retos de la semana 30 de 2025
Calcular el número máximo de raíces reales distintas que puede tener un
polinomio no nulo $P$ que verifique la siguiente propiedad: el producto de dos raíces distintas de $P$ sigue siendo una raíz de $P$.
pistasolución 1info
Pista. Demuestra que no puede haber dos raíces distintas con valor absoluto mayor que $1$ ni dos raíces con valor absoluto estrictamente entre $0$ y $1$.
Solución. En el conjunto $A=(-\infty,1)\cup(1,+\infty)=\{x\in\mathbb{R}:|x|\gt 1\}$ no puede haber más de una raíz. Para probarlo, como todo polinomio tiene un número finito de raíces, habría una raíz $r$ con valor absoluto mayor o igual que el resto de raíces en $A$; si ahora $s$ es otra raíz, entonces $sr$ también es raíz según el enunciado y tiene valor absoluto $|sr|=|s|\cdot |r|\gt |r|$, contradiciendo que $r$ tiene el valor absoluto máximo. De la misma forma, se prueba que en el conjunto $B=(-1,0)\cup(0,1)=\{x\in\mathbb{R}:0\lt|x|\lt 1\}$ hay una única solución (en este caso, sólo hay que considerar la de valor absoluto mínimo).
Hemos visto así que hay un máximo de $5$ raíces: una en $A$, otra en $B$ y las otras tres serían $-1$, $0$ y $1$, los tres puntos que no están ni en $A$ ni en $B$. Sin embargo, no pueden ser las raíces a la vez ya que si $-1$ fuera una raíz y hubiera otra raíz $\alpha\in A$, entonces $-\alpha=(-1)\alpha\in A$ sería una raíz distinta en $A$. Deducimos, por tanto, que hay un máximo de $4$ raíces. Un ejemplo que prueba que $4$ es el máximo posible es el polinomio:
\[p(x)=x(x-1)(x-2)(x-\tfrac{1}{2}).\]
Problema 1120
Las diagonales de un trapecio $ABCD$ se cortan en el punto $O$, siendo $AB$ y $CD$ los lados paralelos. Sabiendo que la diagonal $AC$ mide $7$, que la altura del trapecio mide $4\sqrt{3}$ y que el ángulo $\angle AOB$ es de $60^\circ$, ¿cuáles son los posibles valores del área de $ABCD$?
pistasolución 1info
Pista. Usa trigonometría y relaciones del triángulo $AOB$ en los que puedas usar los datos del enunciado. Para ello, observa que $OAB$ es semejante a $OCD$ y que las medidas $7$ y $4\sqrt{3}$ se obtienen sumando longitudes homólogas de $OAB$ y $OCD$.
Solución. Consideremos la perpendicular común a las rectas $AB$ y $CD$ que pasa por $O$, que las corta en $P$ y $Q$, respectivamente, de forma que $PQ=4\sqrt{3}$. Los triángulos $AOB$ y $COD$ son semejantes ya que tienen el ángulo $O$ común (opuesto por el vértice) y las rectas $AB$ y $CD$ son paralelas. Por tanto, existe una constante de proporcionalidad $\lambda>0$ tal que $CD=\lambda AB$, $CO=\lambda AO$ y $DO=\lambda BO$. Como $OP$ y $OQ$ son alturas correspondientes en estos triángulos semejantes, tenemos que $OQ=\lambda OP$.
El área del triángulo $AOB$ se puede calcular de dos maneras equivalentes:
\[\tfrac{1}{2}AB\cdot OP=\mathrm{Area}(AOB)=\tfrac{1}{2}BO\cdot AO\,\mathrm{sen}(60^\circ)=\tfrac{\sqrt{3}}{4}BO\cdot AO.\]
Multiplicando por $(1+\lambda)$ y usando que
\begin{align*}
AC&=AO+OC=(1+\lambda)AO=7,\\
PQ&=OP+OQ=(1+\lambda)OP=4\sqrt{3},
\end{align*}
según la información del enunciado, la igualdad de áreas se puede reescribir como
\[AB\cdot (1+\lambda)OP=\tfrac{\sqrt{3}}{2}BO\cdot (1+\lambda)AO\ \Leftrightarrow\ \frac{BO}{AB}=\frac{8}{7}.\]
Ahora bien, el teorema del coseno aplicado al triángulo $AOB$ nos dice que
\[AB^2=BO^2+AO^2-2BO\cdot AO\cos(60^\circ)=BO^2+AO^2-BO\cdot AO,\]
Dividiendo por $AB^2$, esto puede reescribirse como
\[1=\left(\frac{BO}{AB}\right)^2+\left(\frac{AO}{AB}\right)^2-\frac{BO}{AB}\cdot \frac{AO}{AB}.\]
Sustituyendo $\frac{BO}{AB}=\frac{8}{7}$ nos queda una ecuación de segundo grado en la incógnita $\frac{AO}{AB}$, que se resuelve fácilmente dando dos soluciones positivas: $\frac{AO}{AB}=\frac{3}{7}$ y $\frac{AO}{AB}=\frac{5}{7}$. Teniendo en cuenta que $AO=\frac{7}{1+\lambda}$, las soluciones anteriores nos dan $(1+\lambda)AB=\frac{49}{3}$ o bien $(1+\lambda)AB=\frac{49}{5}$.
Finalmente, como el área del trapecio está dada por $S=\frac{1}{2}(AB+CD)PQ=\frac{1}{2}(1+\lambda)AB\cdot PQ$ y que $PQ=4\sqrt{3}$ es conocido, llegamos a que las posibles soluciones son
\[S=\frac{98\sqrt{3}}{3}\quad\text{y}\quad S=\frac{98\sqrt{3}}{5}.\]
Las dos soluciones se corresponden con que $C$ se proyecte sobre $AB$.

Retos de la semana 29 de 2025
Sea $P$ un punto del lado $BC$ de un triángulo $ABC$. La paralela por $P$ a $AB$ corta al lado $AC$ en el punto $Q$ y la paralela por $P$ a $AC$ corta al lado $AB$ en el punto $R$. Si la razón entre las áreas de los triángulos $RBP$ y $QPC$ es $k^2$, hallar la razón entre las áreas de los triángulos $ARQ$ y $ABC$.
pistasolución 1info
Pista. Observa que los triángulos $BRP$, $PQC$ y $BAC$ son semejantes y que $ARPQ$ es un paralelogramo.
Solución. Por el paralelismo entre las rectas dadas, está claro que los triángulos $RBP$, $QPC$ y $ABC$ son semejantes ya que tienen sus tres ángulos iguales. También por tener sus lados opuestos paralelos, es fácil darse cuenta de que $ARPQ$ es un paralelogramo, luego $QRQ$ y $PQR$ son triángulos congruentes. Para pasar de $QPC$ a $RBP$ multiplicamos por un factor $k$ (de forma que las áreas se multiplican por $k^2$), luego $BP=k\cdot CP$. De esta forma $BC=(1+k)CP$, luego para pasar de $QPC$ a $ABC$ se multiplica por un factor $1+k$ (y las áreas se multiplican por $(1+k)^2$). Todo esto nos dice que
\begin{align*}
(1+k)^2\mathrm{Área}(RBP)&=\mathrm{Área}(ABC)=\mathrm{Área}(RBP)+\mathrm{Área}(QPC)+2\mathrm{Área}(ARQ)\\
&=\mathrm{Área}(RBP)+k^2\,\mathrm{Área}(RBP)+2\mathrm{Área}(ARQ),
\end{align*}
de donde se tiene que $\mathrm{Área}(ARQ)=k\,\mathrm{Área}(RBP)$. Con esto podemos calcular finalmente
\begin{align*}
\frac{\mathrm{Área}(ARQ)}{\mathrm{Área}(ABC)}=\frac{k\,\mathrm{Área}(RBP)}{(1+k)^2\,\mathrm{Área}(RBP)}=\frac{k}{(1+k)^2}.
\end{align*}
En un triángulo rectángulo de hipotenusa unidad y ángulos respectivos de
$30^\circ$, $60^\circ$ y $90^\circ$, se eligen $25$ puntos cualesquiera. Demostrar que siempre habrá $9$ entre ellos que podrán cubrirse con un semicírculo de radio $\frac{3}{10}$.
pistasolución 1info
Pista. Subdivide el triángulo en tres triángulos rectángulos de hipotenusa menor que $\frac{3}{5}$ y usa el principio del palomar.
Solución. Un triángulo rectángulo puede recubrirse con un semicírculo de diámetro su hipotenusa. Si descomponemos el triángulo en tres triángulos rectángulos de hipotenusa menor que $\frac{3}{5}$, habremos terminado puesto que por el principio del palomar en uno de ellos tienen que encontrarse $9$ de los puntos (si en cada uno hubiera $8$ o menos puntos, entonces el total de puntos no podría exceder $8\cdot 3=24$).
Llamamos $A$ al vértice con el ángulo recto, $B$ al vértice de $30^\circ$ y $C$ al de $60^\circ$. Sea $D$ el punto interior de $BC$ tal que $BE=\frac{3}{5}$ y trazamos la perpendicular a la hipotenusa $BC$ que pasa por $E$ y corta a $BC$ en otro punto $E$. Entonces, tenemos $ABC$ descompuesto como unión de los tres triángulos rectángulos $BDE$, $ACD$ y $BDE$, como se indica en la figura. Ahora bien, $BDE$ tiene hipotenusa $BD=\frac{3}{5}$, mientras que $ACD$ y $BDE$ comparten hipotenusa $CD$. El teorema de Pitágoras nos dice que
\begin{align*}
CD^2&=DA^2+AC^2=(AB-BD)^2+AC^2=(\mathrm{sen}(60)-\tfrac{3}{5})^2+\mathrm{cos}^2(60)\\
&=(\tfrac{\sqrt{3}}{2}-\tfrac{3}{5})^2+(\tfrac{1}{2})^2=\tfrac{34-15\sqrt{3}}{25}
\end{align*}
Tenemos que ver que este número es menor que $\frac{3}{5})^2=\frac{9}{25}$, lo que equivale a ver que $34-15\sqrt{3}\lt 9$ o, más simplificadamente, $5\lt 3\sqrt{3}$. Esto es inmediato ya que, elevando al cuadrado por ser números positivos, la desigualdad se reduce a $25\lt 27$.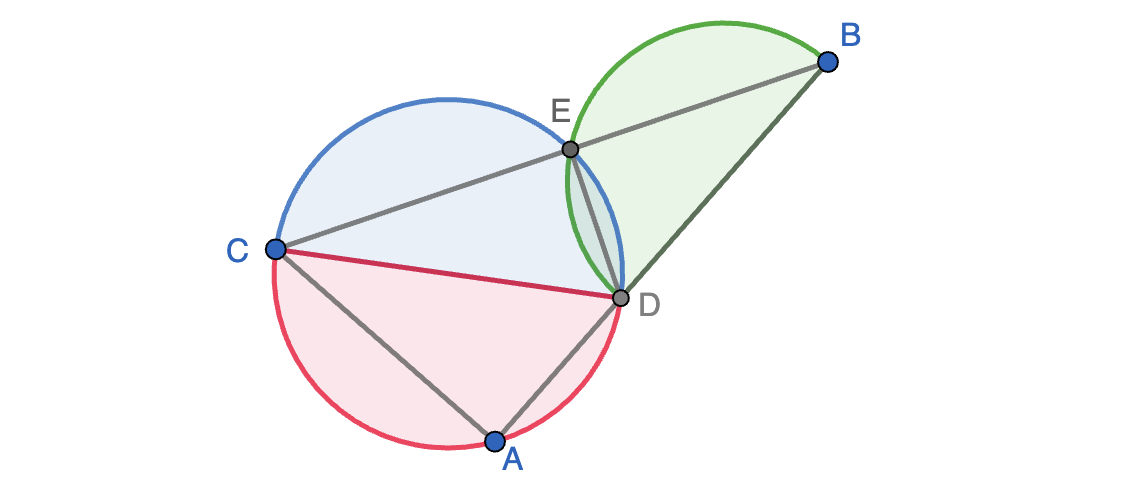
Retos de la semana 28 de 2025
Cada entero positivo se colorea de azul o de rojo de forma que la suma de cualesquiera dos números (no necesariamente distintos) del mismo color, sea azul. Determinar todas las coloraciones posibles del conjunto de los enteros positivos que sigan esta regla.
pistasolución 1info
Pista. Observa que todos los pares deben ir de azul. ¿Qué ocurre con los impares entonces?
Solución. Los números pares tienen que ser necesariamente azules ya que se obtienen como suma de un número (su mitad) consigo mismo. Por tanto, si un número impar $2k+1$ está pintado de azul, se tiene que todos los siguientes impares $2k+3=(2k+1)+2$, $2k+5=(2k+1)+4$,... también tienen que estar pintados azules. Nos quedan, en consecuencia, las siguientes coloraciones:
- Todos los pares de azul y todos los impares de rojo.
- Todos los enteros de azul salvo los primeros $n$ impares, que están pintados de rojo, para cierto $n\geq 0$. En particular, para $n=0$, tendríamos todos los enteros pintados de azul.
Es fácil ver que estas dos formas de pintar cumplen la regla de coloración, luego son las únicas posibilidades.
Sea $ABCD$ un cuadrilátero convexo que tiene los lados $BC$ y $AD$ iguales y no paralelos. Sean $E$ y $F$ puntos en los lados $BC$ y $AD$, respectivamente, que satisfacen $BE=DF$. Las rectas $AC$ y $BD$ se cortan
en $P$, las rectas $BD$ y $EF$ se cortan en $Q$ y las rectas $EF$ y $AC$ se cortan en $R$. Consideremos todos los triángulos $PQR$ que se forman cuando $E$ y $F$ varían. Demuestre que las circunferencias circunscritas a esos triángulos tienen en común otro punto además de $P$.
Sin pistas
Sin soluciones
infoRetos de la semana 27 de 2025
Hallar el menor entero positivo $n$ tal que la suma de los $n$ términos
\[A(n) = 1 + 11 + 111 + \ldots + 11\ldots11\]
sea divisible por $45$.
pistasolución 1info
Pista. Ser divisible por $45$ equivale a ser divisible por $5$ y por $9$.
Solución. Ser divisible por $45$ es lo mismo que ser divisible simultáneamente por $5$ y por $9$. Por un lado tenemos que
\[A(n)\equiv 1+1+1+\ldots+1=n\ (\text{mod }5),\]
luego $A(n)$ es múltiplo de $5$ si y solo si $n$ lo es. Por otro lado,
\[A(n)\equiv 1+2+3+\ldots+n=\frac{n(n+1)}2\ (\text{mod }9),\]
ya que cada número es congruente con la suma de sus cifras módulo $9$ y donde hemos usado además la fórmula conocida para la suma de los $n$ primeros números naturales. Ahora bien, $\frac{n(n+1)}2$ es múltiplo de $9$ cuando $n$ o $n+1$ sean múltiplos de $9$ (ambos no pueden ser múltiplos de $3$ porque son enteros consecutivos). Buscando el primer múltiplo positivo de $5$ tal que $n$ o $n+1$ sean múltiplos de $9$, llegamos rápidamente a que la respuesta a la pregunta del enunciado es $n=35$.
Supongamos que $a,b,c$ son los lados de un triángulo. Probar que
\[a^2(b+c-a)+b^2(c+a-b)+c^2(a+b-c)\leq 3abc.\]
pistasolución 1info
Pista. Si $a,b,c$ son las longitudes de los lados de un triángulo, entonces puedes sustituir $a=x+y$, $b=y+z$ y $c=z+x$ y ahora $x,y,z$ son números reales positivos arbitrarios. Opera para simplificar la expresión resultante.
Solución. Si $a,b,c$ son las longitudes de los lados de un triángulo, entonces podemos sustituir $a=x+y$, $b=y+z$ y $c=z+x$, siendo ahora $x,y,z$ números positivos arbitrarios. Esto nos da la siguiente desigualdad a demostrar
\[2z(x+y)^2+2x(y+z)^2+2y(z+x)^2\leq 3(x+y)(y+z)(x+z).\]
Haciendo todos los productos indicados, nos queda equivalentemente
\[xy^2+x^2y+yz^2+y^2z+zx^2+xz^2\leq 6xyz.\]
Esta última desigualdad es consecuencia de aplicar la desigualdad entre las medias aritmética y geométrica a los seis sumandos (observemos que son números positivos), es decir,
\[\frac{xy^2+x^2y+yz^2+y^2z+zx^2+xz^2}{6}\leq\sqrt[6]{xy^2\cdot x^2y\cdot yz^2\cdot y^2z\cdot zx^2\cdot xz^2}=xyz.\]
Retos de la semana 26 de 2025
Determinar todas las ternas $(x,y,z)$ de números reales que satisfacen el siguiente sistema de ecuaciones:
\[\left.\begin{array}{r}x+y-z=-1\\x^2-y^2+z^2=1\\-x^3+y^3+z^3=-1\end{array}\right\}\]
pistasolución 1info
Pista. Prueba que toda solución cumple $y=-1$.
Solución. Probando con los números $1$ y $-1$, podemos encontrar fácilmente las soluciones $(1,-1,1)$ y $(-1,-1,-1)$. Probaremos que son las únicas y, para ello, comenzaremos viendo que cualquier solución $(x,y,z)$ cumple que $y=-1$.
En efecto, si $y\gt -1$, en la primera ecuación tendríamos que $x\gt z$ y en la tercera que $x\lt z$, lo que nos lleva a una contradicción. Si ocurriera que $y\lt -1$, tendríamos que de la primera ecuación $x-z=-1-y\gt 0$ y, de la tercera, que $-x^3+z^3=-1-y^3\gt 0$, luego volvemos a caer en la misma contradicción. Deducimos entonces que $y=-1$.
Sustituyendo $y=-1$, tenemos que $x=z$ en la primera ecuación y $x^2+z^2=2$ en la segunda, luego $x=z=\pm 1$, de donde obtenemos las soluciones propuestas anteriormente. Observemos que ambas cumplen la tercera ecuación luego son las únicas soluciones.
Sea $ABCD$ un cuadrilátero convexo tal que las rectas $AB$ y $CD$ se cortan en un punto $F$ y las rectas $AD$ y $BC$ se cortan en un punto $E$. Demostrar que las circunferencias circunscritas de los triángulos $BFC$, $AFD$, $DCE$ y $ABE$ tienen un punto en común.
pistasolución 1info
Pista. Considera el punto de corte de dos de las circunferencias y demuestra que pertenece a las otras dos usando repetidamente el arco capaz (¡caza de ángulos!).
Solución. Consideremos las circunferencias circunscritas a los triángulos $ABE$ y $AFD$, que se cortarán en $A$ y en otro punto $P$. Queremos ver que este punto $P$ pertenece a las otras dos circunferencias circunscritas, para lo que vamos a usar la propiedad del arco capaz. Llamaremos $\alpha,\beta,\gamma,\delta$ a los ángulos del cuadrilátero $A,B,C,D$ por comodidad.
Como $ADPF$ es cíclico, tenemos que $\angle APD=\angle AFD=180-\alpha-\delta$ y, como $ABPE$ es cíclico, tenemos que $\angle APB=\angle AEB=180-\alpha-\beta$, luego
\[\angle DPB=\angle DPA+\angle APB=(180-\alpha-\delta)+(180-\alpha-\beta)=360-2\alpha-\beta-\delta=\gamma-\alpha,\]
donde hemos usado que $\alpha+\beta+\gamma+\delta=360$. Ahora bien, como $ADPF$ es cíclico, tenemos que $\angle DPF=180-\angle DAF=180-\alpha$, luego obtenemos que
\[\angle BPF=\angle DPF-\angle APF=(180-\alpha)-(\gamma-\alpha)=180-\gamma=\angle BCF.\]
De este modo, los dos ángulos indicados en rojo en la figura son iguales, luego $P$ está en la circunferencia circunscrita al triángulo $BFC$. Con la circunferencia $DCE$ se razona igual (sólo hay que cambiar $E$ por $F$ y $B$ y $\beta$ por $D$ y $\delta$ en el razonamiento anterior).
Retos de la semana 25 de 2025
Dado un cuadrilátero convexo $ABCD$, se consideran el cuadrilátero $A'B'C'D'$ tal que $A$ es el punto medio de $DA'$, $B$ es el punto medio de $AB'$, $C$ es el punto medio de $BC'$ y $D$ es el punto medio de $CD'$. Demostrar que el área de $A'B'C'D'$ es cinco veces el área de $ABCD$.
pistasolución 1info
Pista. ¿Cuál es la razón entre las áreas de $BB'C'$ y $ABC$?
Solución. El triángulo $BB'C'$ (azul) tiene doble área que el $ABC$ (naranja) ya que tiene base doble $BC'=2BC$ y las mismas alturas respecto de estas bases (las distancias de $A$ y $B'$ a la recta $BC$ coinciden pues el punto medio de $AB'$ pertenece a la recta. De la misma manera, los triángulos $AA'B'$, $CC'D'$ y $DD'A'$ tiene área el doble que las de $ABD$, $BCD$ y $CDA$, respectivamente. Por lo tanto, la suma de las áreas de $AA'B'$, $BB'C'$, $CC'D'$ y $DD'A'$ es cuatro veces la del cuadrilátero $ABCD$. Si le sumamos una vez más el área de $ABCD$, tenemos el área de $A'B'C'D'$ es cinco veces el área de $ABCD$.
Encontrar un conjunto infinito de enteros positivos $S$ tal que la suma de los elementos de cualquier subconjunto finito de $S$ no sea un cuadrado perfecto.
pistasolución 1info
Pista. El siguiente cuadrado perfecto después de $m^2$ es $(m+1)^2=m^2+(2m+1)$, lo que deja $2m$ números que no son cuadrados entre ambos: ¿cómo podemos aprovecharnos de ésto?
Solución. Definamos la sucesión de números $\{x_n\}$ como $x_1=2$ y, para $n\geq 2$,
\[x_n=(x_1+x_2+\ldots+x_{n-1})^2+1.\]
Vamos a probar que el conjunto $S$ formado por todos los números $x_n$ cumple la condición del enunciado. Para ello, tomemos una cantidad finita de ellos $x_{n_1},x_{n_2},\ldots,x_{n_j}$ y demostremos que $N=x_{n_1}+x_{n_2}+\ldots+x_{n_j}$ no es un cuadrado perfecto. Podemos suponer sin perder generalidad que $0\lt n_1\lt n_2\lt\ldots\lt n_j$, luego llamando $A=x_1+x_2+\ldots+x_{n_j-1}$ tenemos que
\[A^2\lt x_{n_j}\leq N\leq x_1+x_2+\ldots+x_{n_j}=A^2+A+1\lt (A+1)^2,\]
lo que nos dice que $N$ está estrictamente entre dos cuadrados consecutivos y, por tanto, no puede ser un cuadrado como queríamos probar.
Nota. Uno puede preguntarse cómo se le ocurre la solución. El truco está en caer en la cuenta de que el siguiente cuadrado a $m^2$ es $(m+1)^2=m^2+2m+1$. Por tanto, si todo elemento es de la forma $m^2+1$ y entre todos los que son menores que él no suman $2m$, la sucesión cumplirá el enunciado. La forma en que lo hemos hecho es una entre una infinidad de posibilidades.
Retos de la semana 24 de 2025
Dado un entero positivo $n$, hallar la suma de todos los enteros positivos
menores que $10n$ que no son múltiplos de $2$ ni de $5$.
pistasolución 1info
Pista. Fíjate que los números que son múltiplos de $2$ son los que terminan en un dígito par y los múltiplos de $5$ los que terminan en dígito $0$ o $5$. Entonces, estás buscando la suma de los que terminan en $1$, $3$, $7$ o $9$.
Solución. Los enteros positivos que no son múltiplos de $2$ ni de $5$ son aquellos cuyo dígito de las unidades es $1,3,7,9$. Hay exactamente $n$ números menores que $10n$ con dígito de las unidades un $j$ dado, a saber:
\[j,10+j,20+j,\ldots 10(n-1)+j.\]
La suma de estos $n$ números es
\[10(1+2+\ldots+(n-1))+nj=5n(n-1)+nj=5n^2+(j-5)n.\]
Por tanto, la suma que estamos buscando es
\[5n^2+(1-5)n+5n^2+(3-5)n+5n^2+(7-5)n+5n^2+(9-5)n=20n^2.\]
Demostrar que en la progresión aritmética $3,7,11,15,\ldots$ hay infinitos números primos.
pistasolución 1info
Pista. Adapta la prueba clásica de Euclides de la infinitud de los números primos suponiendo por reducción al absurdo que solamente hay una cantidad finita de primos de la forma $4k+3$.
Solución. Queremos demostrar que hay infinitos números primos congruentes con $3$ módulo $4$, para lo que adaptaremos la demostración clásica de Euclides suponiendo por reducción al absurdo que sólo hay un número finito de ellos, pongamos $p_1,p_2,\ldots,p_n$. Distinguiremos dos casos:
- Si $n$ es impar, entonces consideramos $N=p_1p_2\cdots p_n+4$, que es impar y congruente con $3$ módulo $4$. Por lo tanto, $N$ tendrá algún factor primo congruente con $3$ (observamos que $2$ no es un factor de $N$ y que no puede tener únicamente factores primos congruentes con $1$ pues el propio $N$ sería congruente con $1$ módulo $4$). Como $p_1,p_2,\ldots,p_n$ son todos los primos congruentes con $3$, esto quiere decir que $N$ será divisible por un $p_i$, lo que nos dice que $p_i$ también tiene que dividir a $4$, pero esto es una contradicción ya que $p_i\neq 2$.
- Si $n$ es par, entonces consideramos $N=p_1p_2\cdots p_n+2$, que vuelve a ser impar y congruente con $3$ módulo $4$. El mismo razonamiento anterior nos da una contradicción similar.
Retos de la semana 23 de 2025
Para cada uno de los números naturales entre $1$ y $10^9$, calculamos reiteradamente la suma de sus dígitos hasta reducirlos a un número de un sólo dígito. ¿Encontramos más unos o doses entre los $10^9$ resultados?
pistasolución 1info
Pista. Trabaja módulo $9$.
Solución. La suma de los dígitos de un número tiene el mismo resto que el número al dividirla por $9$. Por tanto, el dígito que resulta al final de hacer sumas reiteradas de dígitos es el propio resto del número o bien $9$ (si el resto es $0$). Entonces, se trata de ver si hay más números que dan resto $1$ o más números que dan resto $2$ del $1$ al $10^9$. Como empezamos en $1$ y terminamos en $10^9$, ambos dan resto $1$ y el resto se repite periódicamente, deducimos que hay exactamente un número más que da resto $1$ que números que dan resto $2$. Por lo tanto, habrá más unos entre los $10^9$ resultados.
Determina todas las funciones $f:\mathbb{N}_0\to\mathbb{N}_0$, siendo $\mathbb{N}_0=\{0, 1, 2, 3,\ldots\}$ el conjunto de enteros no negativos, que verifican simultáneamente las siguientes dos condiciones:
- $f(n+2)-f(n) = 4n + 6$ para todo $n\in\mathbb{N}_0$.
- $f(2022)-f(2021) = 4044$.
pistasolución 1info
Pista. Observa que la función está determinada por los valores de $f(0)$ y $f(1)$
Solución. Escribimos la ecuación funcional del apartado para todos los números pares desde $n=0$ hasta $n=2k$. Obtenemos así las siguientes ecuaciones
\begin{align*}
f(2)-f(0)&=6&&=6+8\cdot 0\\
f(4)-f(2)&=14&&=6+8\cdot 1\\
f(6)-f(4)&=22&&=6+8\cdot 2\\
&\ \vdots\\
f(2k+2)-f(2k)&=8k+6&&=6+8\cdot k
\end{align*}
Sumando estas $k+1$ ecuaciones se cancelan casi todos los términos de las partes izquierdas (suma telescópica) y nos queda
\[f(2k+2)-f(0)=6(k+1)+8(0+1+\ldots+k)=6(k+1)+4k(k+1)=(2k+2)(2k+3).\]
Hacemos ahora el mismo razonamiento con las $k$ ecuaciones que se obtienen desde $n=1$ hasta $n=2k-1$, que están dadas por
\begin{align*}
f(3)-f(1)&=10&&=10+8\cdot 0\\
f(5)-f(3)&=18&&=10+8\cdot 1\\
f(7)-f(5)&=26&&=10+8\cdot 2\\
&\ \vdots\\
f(2k+1)-f(2k-1)&=8k+2&&=10+8\cdot (k-1)
\end{align*}
Sumando obtenemos que
\[f(2k+1)-f(1)=10k+8(0+1+2+\ldots+(k-1))=10k+4(k-1)k=(2k+3)2k.\]
Si llamamos $a=f(0)$ y $b=f(1)$, podemos expresar la función como
\[f(n)=\begin{cases}
n(n+1)+a&\text{si }n\text{ es par},\\
(n-1)(n+2)+b&\text{si }n\text{ es impar}.
\end{cases}\]
Observamos además que $f(n)\geq 0$ para todo $n\geq 0$ precisamente cuando $a\geq 0$ y $b\geq 0$. Calculamos finalmente $f(2022)=2022\cdot 2023+a$ y $f(2021)=2020\cdot 2022+b$, luego debe cumplirse que
\[4044=f(2022)-f(2021)=2022\cdot 2023+a-2020\cdot 2023-b\ \Leftrightarrow\ b=2+a.\]
Esto nos dice que las soluciones al problema son las funciones
\[f(n)=\begin{cases}
n(n+1)+a&\text{si }n\text{ es par},\\
(n-1)(n+2)+2+a&\text{si }n\text{ es impar},
\end{cases}\]
para todo $a\geq 0$ (se comprueba que todas ellas cumplen las condiciones).
Retos de la semana 22 de 2025
Se sabe que el número de soluciones reales del sistema
\[\left\{\begin{array}{l}(y^2+6)(x-1)=y(x^2+1),\\
(x^2+6)(y-1)=x(y^2+1),\end{array}\right.\]
es finito. Probar que este sistema tiene un número par de soluciones reales.
pistasolución 1info
Pista. Si $(x,y)$ es una solución, entonces $(y,x)$ también es una solución. ¿Qué pasa con las soluciones de la forma $(x,x)$?
Solución. Como intercambiar $x$ e $y$ no hace otra cosa que cambiar de orden las ecuaciones, tenemos que $(x,y)$ solución si, y sólo si, $(y,x)$ lo es. Esto nos da un número par de soluciones con $x\neq y$. Nos queda encontrar las soluciones con $x=y$, en cuyo caso las dos ecuaciones son la misma y queda
\[(x^2+6)(x-1)=x(x^2+1)\ \Leftrightarrow\ x^2-5x+6=0,\]
que tiene dos soluciones reales ($x=2$ y $x=3$), que también es un número par.
Nota. Es interesante preguntarse si realmente es que no se pueden calcular todas las soluciones, pero no es así. Si obviamos las soluciones $(2,2)$ y $(3,3)$ obtenidas, podemos sumar y restar las dos ecuaciones dadas para obtener el sistema cuadrático siguiente (tras simplificar el factor $x-y$ que aparece en la diferencia):
\[\left\{\begin{array}{l}
2xy-x-y=7\\
x^2+y^2-5x-5y=-12
\end{array}\right.\]
Despejando $x=\frac{7+y}{2y-1}$ en la primera ecuación y sustituyendo en la segunda, obtenemos la ecuación cuadrática $y^4-6 y^3+15 y^2-26 y+24=0$, cuyas únicas soluciones reales son $y=2$ e $y=3$ (se obtienen por Ruffini). Por tanto, el sistema del enunciado tiene cuatro soluciones: $(2,2)$, $(3,3)$, $(2,3)$ y $(3,2)$.
¿Existe algún triángulo tal que las medidas de sus lados son tres números enteros consecutivos y el ángulo mayor es el doble que el menor? Si existe, determinar sus medidas.
pistasolución 1info
Pista. Fíjate en que los lados están ordenados igual que sus ángulos opuestos. Utiliza los teoremas del seno y el coseno para obtener relaciones entre los lados y los ángulos.
Solución. Pongamos que los lados miden $n-1$, $n$ y $n+1$ y que el ángulo menor es $\alpha$ y el mayor $2\alpha$. Esto nos dice que $2\alpha$ es el ángulo opuesto a $n+1$ y $\alpha$ el opuesto a $n-1$ ya que los ángulos guardan el mismo orden que sus lados opuestos. Por tanto, el teorema del seno nos dice que
\[\frac{\mathrm{sen}(\alpha)}{n-1}=\frac{\mathrm{sen}(2\alpha)}{n+1}=\frac{2\mathrm{sen}(\alpha)\cos(\alpha)}{n+1}\ \Longrightarrow\ \cos(\alpha)=\frac{n+1}{2(n-1)}.\]
Ahora bien, el teorema del coseno aplicado al lado de longitud $n-1$ nos dice que
\[(n-1)^2=n^2+(n+1)^2-2n(n+1)\cos(\alpha)=2n^2+2n+1-\frac{n(n+1)^2}{n-1}.\]
Operando y simplificando, la ecuación anterior equivale a $n(n-5)=0$, lo que nos da como única posibilidad $n=5$ (el triángulo de lados $4$, $5$ y $6$).
Resta por ver si este triángulo cumple la propiedad. De nuevo por el teorema del coseno, tenemos que el ángulo $\alpha$ opuesto al lado de longitud $4$ cumple
\[\cos(\alpha)=\frac{5^2+6^2-4^2}{2\cdot 5\cdot 6}=\frac{3}{4}.\]
Por su parte, el ángulo $\beta$ opuesto al lado de longitud $6$ cumple
\[\cos(\beta)=\frac{4^2+5^2-6^2}{2\cdot 4\cdot 5}=\frac{1}{8}=2\cos^2(\alpha)-1=\cos(2\alpha).\]
Deducimos que $\beta=2\alpha$, luego en este triángulo el ángulo mayor es el doble del menor y respondemos así afirmativamente a la pregunta del enunciado.
Retos de la semana 21 de 2025
En un triángulo $ABC$, sabemos que la altura que pasa por $A$ es mayor o igual que el lado $BC$ y que la altura que pasa por $B$ es mayor o igual que el lado $AC$. Encontrar los ángulos de dicho triángulo.
pistasolución 1info
Pista. Usa el teorema de Pitágoras con las alturas y los lados adyacentes para obtener desigualdades entre los lados.
Solución. Llamemos $a,b,c$ a los lados del triángulo opuestos a los vértices $A,B,C$, respectivamente, y llamemos $h_a$ y $h_b$ a las alturas sobre los lados $a$ y $b$, respectivamente. Como la distancia de $A$ a la recta $BC$ es $h_a$, se tiene que $b\geq h_a\geq a$. Análogamente, como la distancia de $B$ a la recta $AC$ es $h_b$, se tiene que $a\geq h_b\geq b$. Esto nos dice que $a=b$ y también que la distancia de $A$ a la recta $BC$ se realiza en $C$ (es decir, $C$ es el pie de la altura $h_a$). En particular, el ángulo $\angle ACB$ es recto y los ángulos $\angle BAC$ y $\angle ABC$ son de $45º$ por ser $a=b$.
Dado un subconjunto $A$ formado por $10$ elementos del conjunto $\{10,11,\ldots,99\}$, demostrar que existen dos subconjuntos disjuntos de $A$ cuyos elementos suman la misma cantidad.
pistasolución 1info
Pista. Usa el principio del palomar: ¡hay más subconjuntos que sumas posibles!
Solución. El conjunto $A$ tiene $10$ elementos, luego hay $2^{10}-1=1023$ subconjuntos distintos de $A$ no vacíos. Por otro lado, la suma mínima de elementos de uno de tales subconjuntos es $10+11+\ldots+19=185$ y la suma máxima $90+91+\ldots+99=945$, luego no hay más de $945-184=771$ sumas posibles distintas. Por el principio del palomar, habrá dos subconjuntos $B$ y $C$ de $A$ con la misma suma. Ahora basta con eliminar de $B$ y $C$ los elementos comunes, con lo que obtendremos los subconjuntos que queremos.
Retos de la semana 20 de 2025
¿Cuántas ternas ordenadas de números enteros y positivos $(a,b,c)$ distintos de la unidad hay tales que $abc=7^{39}$?
pistasolución 1info
Pista. El problema equivale a encontrar soluciones enteras $x,y,z\geq 1$ de la ecuación $x+y+z=39$. Para cada valor de $x$ entre $1$ y $37$, ¿cuántos valores distintos puede tomar el par $(y,z)$?
Solución. Los números $a,b,c$ sólo pueden tener al 7 como factor primo, luego podemos escribir $a=7^x$, $b=7^y$ y $c=7^z$, lo que nos permite escribir $7^{39}=abc=7^x7^y7^z=7^{x+y+z}$. Por tanto, el problema equivale a encontrar las ternas $(x,y,z)$ de enteros mayores o iguales que $1$ tales que $x+y+z=39$. Observamos que $x$ debe estar entre $1$ y $37$ y, para cada valor de $x$, hay $38-x$ pares $(y,z)$ tales que $y+z=39-x$, que vienen dados por
\[(1,38-x),(2,37-x),(3,36-x),\qquad (38-x,1).\]
Por tanto, el número de soluciones es
\[\sum_{x=1}^{37}(38-x)=37+36+35+\ldots+1=\frac{37\cdot 38}{2}=703.\]
Nota. El problema también se puede resolver mediante combinaciones con repetición usando separadores. Expresando $x=1+x'$, $y=1+y'$ y $z=1+z'$, tenemos que encontrar la cantidad de ternas $x',y',z'\geq 0$ tales que $x'+y'+z'=36$, lo que equivale a elegir dos separadores en una lista de $36+2=38$ elementos, esto es, el número de soluciones es
\[\binom{38}{2}=\frac{38\cdot 37}{2}=703.\]
Hallar razonadamente un ejemplo de enteros positivos $a$ y $b$ que verifiquen las siguientes dos condiciones:
- $ab(a+b)$ no es divisible por $7$,
- $(a+b)^7-a^7-b^7$ es divisible por $7^7$.
pistasolución 1info
Pista. Observa que $(a+b)^7-a^7-b^7=7ab(a+b)(a^2+ab+b^2)^2$.
Solución. El binomio de Newton nos asegura que
\begin{align*}
(a+b)^7-a^7-b^7&=7(a^6b+3a^5b^2+5a^4b^3+5a^3b^4+3a^2b^5+ab^6)\\
&=7ab(a+b)(a^2+ab+b^2)^2.
\end{align*}
Por lo tanto, si $ab(a+b)$ no es divisible por $7$, necesariamente tendremos que encontrar $a$ y $b$ tales que $a^2+ab+b^2$ sea divisible por $7^3=343$. Curiosamente, si tomamos $b=1$, la ecuación $a=2+a+1=343$ tiene por solución entera positiva $a=18$. Como ni $1$ ni $18$ son múltiplos de $7$, obtenemos que $(a,b)=(18,1)$ es una posible respuesta al problema.
Retos de la semana 19 de 2025
Demostrar que la expresión
\[\frac{n^5-5n^3+4n}{n+2},\]
donde $n$ es un entero, es un entero divisible por $24$.
pistasolución 1info
Pista. Simplificar y factorizar.
Solución. Dividiendo los dos polinomios (o bien utilizando el método de Ruffini para evaluar en $n=-2$), obtenemos que
\[\frac{n^5-5n^3+4n}{n+2}=n^4-2 n^3-n^2+2 n.\]
Este último polinomio se puede factorizar en los enteros sacando factor común $n$ y utilizando de nuevo el método de Ruffini:
\[\frac{n^5-5n^3+4n}{n+2}=(n-2)(n-1)n(n+1).\]
Como es el producto de 4 enteros consecutivos, al menos dos de ellos serán pares, uno de los cuales ha de ser múltiplo de $4$, luego el resultado es múltiplo de $8$. Por el mismo motivo habrá al menos uno de ellos múltiplo de $3$, luego el resultado es múltiplo de $3\cdot 8=24$.
Nota. No podemos asegurar que haya un factor más grande ya que, para $n=3$ la expresión tiene un valor precisamente de $24$.
Sea $f:\mathbb{N}\to\mathbb{N}$ la función definida por
\[f(1)=1,\qquad f(2n+1)=f(2n)+1,\qquad f(2n)=3f(n),\]
para todo entero positivo $n\in\mathbb{N}$. Determinar el conjunto de valores que toma $f$.
pistasolución 1info
Pista. ¿Qué relación hay entre la expresión de $n$ en base $2$ y la de $f(n)$ en base $3$?
Solución. Vamos a probar que si expresamos $n$ en base $2$ con solo ceros y unos, el número $f(n)$ es el que tiene esa misma representación en base $3$. Eso hace que el conjunto de valores que toma $f$ son los números que se escriben solamente con ceros y unos en base $3$, es decir, los números que son suma de potencias distintas de $3$.
Vamos a proceder por inducción completa sobre $n$. El caso base $n=1$ está claro ya que $f(1)=1$ y $1$ se expresa igual en ambas bases. Supongamos entonces que el resultado es cierto hasta cierto valor $n$ y veamos lo que ocurre con $n+1$. Podemos escribir
\[n+1=2^ka_k+\ldots+4a_2+2a_1+a_0,\]
siendo $a_k\ldots a_2a_1a_0$ los dígitos de $n+1$ en base $2$. Distinguimos dos casos según el valor de $a_0$:
- Si $a_0=0$, entonces podemos escribir
\begin{align*}
f(n+1)&=f(2(2^{k-1}a_k+\ldots+2a_2+a_1))=3f(2^{k-1}a_k+\ldots+2a_2+a_1)\\
&=3f(3^{k-1}a_k+\ldots+3a_2+a_1)=3^ka_k+\ldots+9a_2+3a_1,
\end{align*}
donde hemos usado que $2^{k-1}a_k+\ldots+2a_2+a_1=\frac{n-1}{2}\lt n$ y la hipótesis de inducción. Por tanto, tenemos que $f(n+1)$ es el número que tiene los dígitos $a_k\ldots a_2a_1a_0$ en base $3$.
- De forma similar, si $a_0=1$, entonces
\begin{align*}
f(n+1)&=f(2(2^{k-1}a_k+\ldots+2a_2+a_1)+1)=f(2(2^{k-1}a_k+\ldots+2a_2+a_1))+1\\
&=f(2^{k}a_k+\ldots+4a_2+2a_1)+1=3^{k}a_k+\ldots+9a_2+3a_1+1,
\end{align*}
vuelve a ser el número con dígitos $a_k\ldots a_2a_1a_0$ en base $3$. Aquí hemos aplicado la hipótesis de inducción a $n=2^{k}a_k+\ldots+4a_2+2a_1$.
Retos de la semana 18 de 2025
Supongamos que la sucesión \(a_n\) está definida como \(a_1=3\) y \(a_{n+1}=a_n+a_n^2\) para todo natural \(n\). Hallar las dos últimas cifras de \(a_{2000}\).
pistasolución 1info
Pista. Fíjate en que las dos últimas cifras se van repitiendo periódicamente. Calcula unos cuantos términos para ver qué les ocurre.
Solución. Las dos últimas cifras de \(a_n\) sólo dependen de las dos últimas cifras de \(a_{n-1}\), luego bastará calcular algunos términos hasta que se repitan las dos últimas cifras. En realidad, esto podría ser un proceso muy largo, pero da la casualidad de que obtenemos la siguiente sucesión de últimas cifras:
\[03\to 12\to 56\to 92\to 56\to 92\to 56\to 92\to\ldots\]
De esta forma, salvo los dos primeros, vemos que los siguientes se repiten por parejas. En particular, las dos últimas cifras de \(a_{2000}\) son las mismas que las de \(a_4\), luego la respuesta a la pregunta es \(92\).
Demostrar que en un triángulo la distancia de un vértice cualquiera al ortocentro es el doble de la distancia del circuncentro al lado opuesto a ese vértice.
pistasolución 1info
Pista. Hay muchas formas de demostrar este resultado. Considera el triángulo que se forma entre el circuncentro, el punto medio del lado y un vértice de ese lado. Este triángulo lo puedes duplicar haciendo homotecia de razón $2$ respecto de ese vértice.
Solución. Consideremos un triángulo $ABC$, su circuncentro $O$ y su ortocentro $H$. Si llamamos $M$ al punto medio del lado $BC$, tendremos que demostrar que $AH=2BC$. Para ello, trazamos el diámetro de la circunferencia circunscrita que pasa por $B$ y su punto diametralmente opuesto, que llamaremos $P$, como se indica en la figura. Por ser $BP$ un diámetro, se tiene que $PC$ es perpendicular a $BC$ y, por tanto, paralela a la mediatriz $OM$. Entonces, los triángulos $BOM$ y $BPC$ son semejantes y se cumple que $PC=2OM$, luego tendremos que demostrar que $PC=AH$. Esto último se sigue de que $APCH$ es un paralelogramo ya que $PC$ es paralela a la altura $AH$ y $AP$ es paralela a la altrua $CH$ (ya que el ángulo $\angle BAP$ es recto por comprender al diámetro $BP$).
Nota. Este es un resultado relativamente conocido en el ámbito de la geometría de olimpiadas. ¿Sabrías probar que $AH=2R\cos A$ y $OM=R\cos A$, siendo $R$ el radio de la circunferencia circunscrita? ¿Sabrías probar a partir de este resultado que las rectas $OA$ y $MH$ se cortan en un punto de la circunferencia circunscrita?
Retos de la semana 17 de 2025
Sea $ABCD$ un paralelogramo y sea $M$ un punto en la diagonal $BD$ que cumple $MD=2BM$. Las rectas $AM$ y $BC$ se cortan en un punto $N$. ¿Cuál es el
cociente entre el área del triángulo $MND$ y el área del paralelogramo $ABCD$?
pistasolución 1info
Pista. Observa que $N$ es el punto medio de $BC$.
Solución. Los triángulos $AMD$ y $BMN$ son semejantes (están en posición de Thales ya que $AD$ y $BC$ son paralelas) y la razón de semejanza es $\frac{1}{2}$ ya que el enunciado nos dice que $MD=2BM$. Por lo tanto, $BN=\frac{1}{2}AD=\frac{1}{2}BC$ y tenemos que $N$ es el punto medio de $BC$. De esta forma, el área $BCD$, que es la mitad de la del paralelogramo, es a su vez el doble del área de $DBN$ (por tener la misma base y altura doble). Por otro lado, el área de $DMN$ es el doble de la de $BMN$ (ya que tiene doble base e igual altura). Todo esto nos dice que
\begin{align*}
\mathrm{Area}(ABCD)&=2\,\mathrm{Area}(BCD)=4\,\mathrm{Area}(BND)\\
&=4(\mathrm{Area}(MND)+\mathrm{Area}(MNB))\\
&=4(\mathrm{Area}(MND)+\tfrac{1}{2}\mathrm{Area}(MND))=6\,\mathrm{Area}(MND).
\end{align*}
Deducimos así que
\[\frac{\mathrm{Area}(MND)}{\mathrm{Area}(ABCD)}=\frac{1}{6}.\]
Octavio escribe un entero $n\geq 1$ en una pizarra y luego inicia un proceso en el que en cada paso borra el número entero $k$ escrito en la pizarra y lo reemplaza por uno de los siguientes números, siempre que el resultado sea entero:
\[3k-1,\qquad 2k+1,\qquad \frac{k}{2}.\]
Demostrar que para todo entero $n\geq 1$, Octavio puede llegar a escribir en la pizarra el número $3^{2023}$ en una cantidad finita de pasos.
pistasolución 1info
Pista. Demuestra que siempre puede llegar a $1$ y luego busca la forma de multiplicar sucesivamente por $3$.
Solución. Llamemos (1) al reemplazo $k\mapsto 3k-1$, (2) al reemplazo $k\mapsto 2k+1$ y (3) al reemplazo $k\mapsto\frac{k}{2}$. Observemos las siguientes cadenas de reemplazos válidas para cualquier entero $m\geq 0$ (es decir, distinguimos casos dependiendo del resto módulo $4$):
\begin{align*}
4m&\stackrel{(3)}{\longmapsto}2m,\\
4m+1&\stackrel{(2)}{\longmapsto}8m+3\stackrel{(1)}{\longmapsto}24m+8\stackrel{(1)}{\longmapsto}12m+4\stackrel{(1)}{\longmapsto}6m+2\stackrel{(1)}{\longmapsto}3m+1,\\
4m+2&\stackrel{(1)}{\longmapsto}2m+1,\\
4m+3&\stackrel{(1)}{\longmapsto}12m+8\stackrel{(1)}{\longmapsto}6m+4\stackrel{(3)}{\longmapsto}3m+2.
\end{align*}
Todas estas transformaciones acaban con un número estrictamente menor que el inicial salvo si empezamos con el $1=4\cdot 0+1$, caso en el que acabamos con el propio $1$. De este modo, aplicando reiteradamente estas cadenas de reemplazos podemos empezar en cualquier número $n$ y terminar en el $1$.
El resto de la demostración será ver que empezando por $1$ podemos multiplicar por $3$ sucesivamente para conseguir cualquier potencia de $3$. Esto es consecuencia de la siguiente cadena de reemplazos:
\[3^a\stackrel{(1)}{\longmapsto}3^{a+1}-1\stackrel{(3)}{\longmapsto}\frac{3^{a+1}-1}{2}\stackrel{(2)}{\longmapsto}3^{a+1},\]
donde la fracción es realmente un número entero ya que $3^{n+1}-1$ es par. Por lo tanto, podemos empezar en $1=3^0$ y pasar sucesivamente a $3^1,3^2,3^3,\ldots$ hasta llegar a $3^{2023}$.
Retos de la semana 16 de 2025
En una reunión hay 201 personas de 5 nacionalidades diferentes. Se sabe que, en cada grupo de 6, al menos dos tienen la misma edad. Demostrar que hay al menos 5 personas del mismo país, de la misma edad y del mismo sexo.
pistasolución 1info
Pista. Observa que sólo puede haber $5$ edades distintas.
Solución. Observemos que a lo sumo hay \(5\) edades distintas entre todos los participantes pues, en caso contrario, no se cumpliría el enunciado pues basta tomar \(5\) personas fijas e ir variando la sexta para formar grupos y en cada uno de ellos una edad ha de repetirse. En definitiva, tenemos \(5\cdot 5\cdot 2=50\) posibilidades distintas en cuanto a sexo, nacionalidad y edad para una persona. Como hay \(201=4\cdot 50+1\) personas en total, el principio del palomar nos asegura que hay cinco que comparten estas tres características.
Probar que $2014^{2013}-1013^{2013}-1001^{2013}$ es múltiplo de
$2014^3−1013^3−1001^3$.
pistasolución 1info
Pista. Aunque $p(x)=(x+y)^n-x^n-y^n$ no es en general divisible entre $q(x)=(x+y)^3-x^3-y^3=3xy(x+y)$, pensar en el problema como si se tratara de dividir polinomios puede ayudarte (observa que el resultado se obtendría para $n=2013$, $x=1013$ e $y=1001$).
Solución. Vamos analizar si $(x+y)^{2n+1}-x^{2n+1}-y^{2n+1}$ es múltiplo de $(x+y)^3-x^3-y^3$ para dos enteros $x,y\in\mathbb{Z}$ y $n\in\mathbb{N}$. Para ello, observamos que $(x+y)^3-x^3-y^3=3xy(x+y)$ y, desarrollamos por el binomio de Newton, podemos factorizar
\begin{align*}
(x+y)^{2n+1}-x^{2n+1}-y^{2n+1}&=\binom{2n+1}{1}x^{2n}y+\binom{2n+1}{2}x^{2n-1}y^2+\ldots+\binom{2n+1}{2n}xy^{2n}\\
&=xy\left(\binom{2n+1}{1}x^{2n-1}+\binom{2n+1}{2}x^{2n-2}y+\ldots+\binom{2n+1}{2n}y^{2n-1}\right)
\end{align*}
Si vemos el último paréntesis grande como un polinomio $p(x)$ para un valor fijo de $y$, tenemos además que
\begin{align*}
p(-y)&=\binom{2n+1}{1}(-y)^{2n-1}+\binom{2n+1}{2}(-y)^{2n-2}y+\ldots+\binom{2n+1}{2n}y^{2n-1}\\
&=y^n\left(-\binom{2n+1}{1}+\binom{2n+1}{2}-\ldots+\binom{2n+1}{2n}\right)=0
\end{align*}
ya que la suma alternada de números combinatorios es cero. Esto nos dice que podemos factorizar como polinomios $p(x)=(x+y)q(x,y)$, luego podemos factorizar $(x+y)^{2n+1}-x^{2n+1}-y^{2n+1}=xy(x+y)q(x,y)$. Nos falta por ver que podemos sacar también el factor $3$ y para ello haremos $x=1013$ e $y=1001$, lo que nos da
\[(x+y)^{2n+1}-x^{2n+1}-y^{2n+1}\equiv 2^{2n+1}-1^{2n+1}-1^{2n+1}=2\cdot 1^{2n}-1-1\equiv 0\ (\text{mod }3).\]
Sin embargo, tenemos que $xy(x+y)\equiv 1\cdot 1\cdot 2\not\equiv 0\ (\text{mod }3)$, luego $(x+y)^{2n+1}-x^{2n+1}-y^{2n+1}$ es múltiplo de $3xy(x+y)$ para todo $n\in\mathbb{N}$, en particular, para $n=1006$.
Nota. No es cierto en general que $(x+y)^{2n+1}-x^{2n+1}-y^{2n+1}$ sea múltiplo de $(x+y)^3-x^3-y^3=3xy(x+y)$ y el problema justamente es el $3$ final. No es difícil completar el argumento para ver que esta propiedad es cierta para todo $n$ si, y sólo si, $x\equiv y\equiv 1$ o bien $x\equiv y\equiv 2$ (mod $3$).
Retos de la semana 15 de 2025
Encontrar todos los enteros positivos $n$ de $4$ cifras tales que todos sus
dígitos son cuadrados perfectos y $n$ es múltiplo de $2$, $3$, $5$ y $7$.
pistasolución 1info
Pista. El dígito de las unidades de $n$ está claro cuál tiene que ser. Fíjate en lo que tienen que cumplir los otros dígitos para que sea múltiplo de $3$ y $7$.
Solución. Al ser múltiplo de $2$ y de $5$, tiene que ser múltiplo de $10$ y, por tanto, la cifra de las unidades será $0$. Pongamos entonces que $n=1000a+100b+10c$. Que sea múltiplo de $3$ nos dice que $a+b+c$ es múltiplo de $3$. Ahora bien, los dígitos pueden ser únicamente $0,1,4,9$ y $a\neq 0$. Como $1$ y $4$ dan resto $1$ al dividirlos entre $3$, $a+b+c$ es múltiplo de $3$ únicamente si los tres dígitos son ceros y nueves(con $a\neq 0$) o los tres son unos y cuatros. Por otro lado, que sea múltiplo de $7$ nos dice que $6a+2b+3c$ es múltiplo de $7$. Distingamos casos según el valor de $a$:
- Si $a=9$, entonces $54+2b+3c$ tiene que ser múltiplo de $7$; como en este caso $b$ y $c$ son cada uno cero o nueve, llegamos fácilmente a que ninguna elección de $b$ y $c$ cumplen estas condiciones.
- Si $a=1$, entonces $6+2b+3c$ debe ser múltiplo de $7$; como en este caso $b$ y $c$ son iguales a uno o cuatro, comprobamos fácilmente que tampoco hay elección que nos dé un múltiplo de $7$.
- Por último, si $a=4$, entonces $24+2b+3c$ debe ser múltiplo de $7$ y también tenemos que $b$ y $c$ son iguales a uno o cuatro. Comprobamos fácilmente que $b=4$ y $c=1$ es la única posibilidad para que esto ocurra.
Concluimos que $n=4410$ es el único número que cumple las condiciones dadas.
Nota. En realidad, tenemos que el número es múltiplo de $210$ luego no es descabellado escribir rápidamente los $43$ múltiplos de $21$ entre $105=5\cdot 21$ y $987=47\cdot 21$ para simplemente chequear cuáles tienen únicamente dígitos $0,1,4,9$. Estos múltiplos son: 105, 126, 147, 168, 189, 210, 231, 252, 273, 294, 315, 336, 357, 378, 399, 420, 441, 462, 483, 504, 525, 546, 567, 588, 609, 630, 651, 672, 693, 714, 735, 756, 777, 798, 819, 840, 861, 882, 903, 924, 945, 966, 987.
Determinar todas las ternas de números reales $(x,y,z)$ que cumplen el siguiente sistema de ecuaciones:
\[\left\{\begin{array}{l}
xyz=8,\\
x^2y+y^2z+z^2x=73,\\
x(y-z)^2+y(z-x)^2+z(x-y)^2=98.
\end{array}\right\}\]
pistasolución 1info
Pista. Demuestra que $(x-y)(y-z)(z-x)=0$.
Solución. Desarrollando los cuadrados en la tercera ecuación y usando las dos primeras se llega fácilmente a que
\[xy^2+yz^2+zx^2=73.\]
Observemos que esta ecuación es muy parecida a la segunda del enunciado pero los cuadrados están en el otro factor. Restando la segunda ecuación del enunciado y esta que hemos obtenido, llegamos a que
\[0=73-73=xy^2+yz^2+zx^2-x^2y-y^2z-z^2x=(y-x)(z-y)(x-z).\]
Por lo tanto, dos de las incógnitas deben ser iguales, pongamos que $y=z$ sin perder generalidad. Entonces, las tres ecuaciones del enunciado se transforman en las dos siguientes:
\[\left.\begin{array}{r}xy^2=8\phantom{3}\\x^2y+y^3+xy^2=73\end{array}\right\}\]
(la tercera ecuación ya no nos hace falta porque es redundante). Esto nos dice que $x^2y+y^3=65$ y, multiplicando por $y^3$, tenemos que $64+y^6=(xy^2)^2+y^6=65y^3$. En consecuencia, $y$ debe ser solución de la ecuación bicúbica $y^6-65y+64=0$, que puede factorizarse como $(y^3-1)(y^3-64)=0$, lo que nos da las soluciones $y=1$ e $y=4$. Como $xy^2=8$ y $z=y$, tenemos que $(x,y,z)=(8,1,1)$ o bien $(x,y,z)=(\tfrac{1}{2},4,4)$. Ahora bien, cualquier permutación de las variables también da una solución (hemos roto la simetría al suponer que $y=z$), luego tenemos seis soluciones para $(x,y,z)$:
\[(8,1,1),\quad (1,8,1),\quad (1,1,8),\quad (\tfrac{1}{2},4,4),\quad (4,\tfrac{1}{2},4),\quad (4,4,\tfrac{1}{2}).\]
Retos de la semana 14 de 2025
Sabiendo que los polinomios
\[\begin{array}{c}
2x^5-13x^4+4x^3+61x^2+20x-25,\\
x^5-4x^4-13x^3+28x^2+85x+50,
\end{array}\]
tienen dos raíces dobles comunes, determinar todas sus raíces.
pistasolución 1info
Pista. Resta al primer polinomio el doble del segundo para obtener un polinomio de grado 4 que debe ser, salvo un factor constante, un cuadrado perfecto.
Solución. Si al primer polinomio le restamos el doble del segundo obtenemos el polinomio
\[-5(x^4-6x^3-x^2+30x+25),\]
que también debe tener las mismas raíces comunes a los polinomios originales. Haciendo la división de cada uno de los polinomios dados dentre $x^4-6x^3-x^2+30x+25$, obtenemos que
\begin{align*}
2 x^5 - 13 x^4 + 4 x^3 + 61 x^2 + 20 x - 25&=(2x-1)(x^4-6x^3-x^2+30x+25),\\
x^5 - 4 x^4 - 13 x^3 + 28 x^2 + 85 x + 50&=(x+2)(x^4-6x^3-x^2+30x+25)
\end{align*}
Como se trata de dos raíces dobles, deducimos además $x^4-6x^3-x^2+30x+25$ debe ser un polinomio cuadrado perfecto, luego expresamos
\[x^4-6x^3-x^2+30x+25=(x^2+ax+b)^2=x^4+2ax^3+(a^2+2b)x^2+2abx+b^2,\]
de donde obtenemos que $a=-3$ y $b=-5$ sin más que comparar coeficientes. Como el polinomio $x^2-3x-5$ tiene raíces $\frac{1}{2}(3\pm\sqrt{29})$, deducimos que estas son las dos raíces dobles comunes a los polinomios originales, mientras que la quinta raíz del primer polinomio es $\frac{1}{2}$ y la quinta raíz del segundo polinomio es $-2$.
¿Qué valores han de tener los ángulos $\alpha$, $\beta$ y $\gamma$ de un triángulo $T$ para que este se pueda dividir en tres triángulos congruentes entre sí?
pistasolución 1info
Pista. Observa que si para subdividir unimos un vértice con un punto del lado opuesto, entonces necesariamente este segmento tiene que ser perpendicular al lado.
Solución. Hay cuatro formas esencialmente distintas de dividir un triángulo en tres triángulos, que está indicadas en la figura de abajo. Sin embargo, nos damos cuenta de que si un segmento termina en el interior de un lado y no es perpendicular a dicho lado, entonces forma dos ángulos suplementarios distintos. Estos dos ángulos deben ser dos de los ángulos de cada triángulo semejante pero un triángulo no puede tener dos ángulos que sumen $180^\circ$. Esto descarta directamente los casos III y IV y restringe el caso II. Veamos directamente qué restricciones adicionales nos da el hecho de que los tres triángulos deben tener ángulos iguales.
- Caso I. Tenemos un vértice interior, en el que se forman al menos dos ángulos obtusos, que deben ser iguales, y el tercero debe ser igual también ya que suma con uno de los obtusos más de $180^\circ$. Hay dos posibles configuraciones para los otros seis ángulos de los tres triángulos, que hemos llamado casos I.a y I.b. En el caso I.a, como la suma de los ángulos de $T$ es $180^\circ$, llegamos a que el ángulo verde más el amarillo suman $60^\circ$, luego $T$ es equilátero. En el caso I.b, el triángulo $T$ es isósceles, luego los ángulos amarillo y verde deben coincidir y también llegamos a que $T$ es equilátero.
- Caso II. Hay esencialmente tres configuraciones para los ángulos que no son rectos, que se indican en los casos II.a, II.b y II.c. En el caso II.a, dos verdes suman $90^\circ$, de donde se tiene que tanto el verde como el amarillo deben ser $45^\circ$ y $T$ es un triángulo rectángulo isósceles. En el caso II.b, el verde y el amarillo suman $90^\circ$, luego $T$ es en principio un triángulo rectángulo cualquiera. En el caso II.c, tenemos que $T$ es un triángulo isósceles cualquiera.
Tenemos, por tanto, que los únicos triángulos que pueden admitir la subdivisión son los triángulos rectángulos y los triángulos isósceles. Sin embargo, las subdivisiones que nos salen nos dan triángulos congruentes solamente en el caso del triángulo equilátero. Subdividiendo este último uniendo cada vértice con el centro, confirmamos que los triángulos equiláteros son las únicas soluciones.
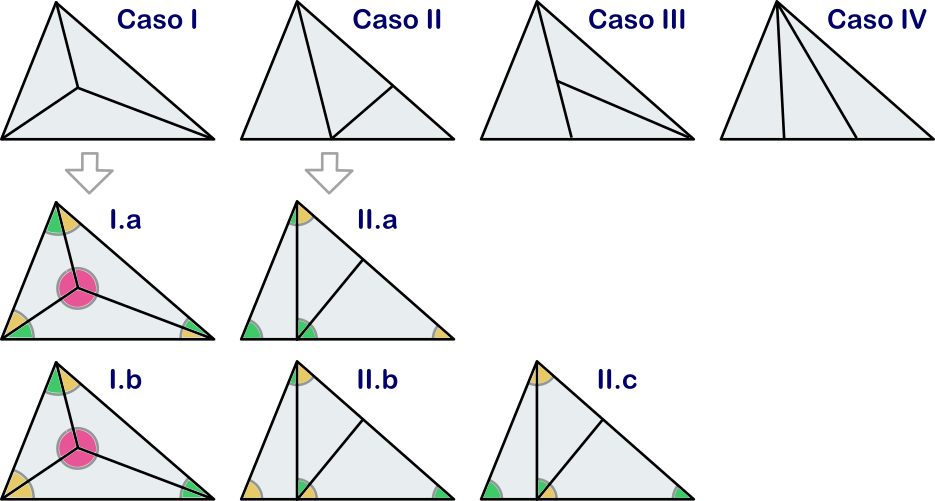
Nota. Hemos probado, de hecho, que los únicos triángulos que se pueden subdividir en tres triángulos semejantes son los triángulos rectángulos y los triángulos isósceles.
Retos de la semana 13 de 2025
Sea $ABC$ un triángulo rectángulo isósceles con el ángulo recto en $C$ y los catetos de longitud $2$. Un arco de círculo $\ell$ con centro $A$ divide al triángulo en dos partes de la misma área, mientras que el arco de círculo $m$ con centro en $B$ es tangente a $\ell$ en un punto de la hipotenusa $AB$. Hallar el área de la porción del triángulo no cubierta por los sectores circulares correspondientes a los dos arcos.
pistasolución 1info
Pista. Calcula primero el radio del arco $\ell$ y luego el radio del arco $m$, con lo que podrás calcular el área de los sectores circulares.
Solución. El área del triángulo es $2$ y el área del sector circular de arco $\ell$ (en azul en la figura) es $\frac{1}{8}\pi r^2$, siendo $r$ su radio. Esto viene de que es un octavo del círculo de radio $r$ ya que el ángulo $A$ del triángulo rectángulo isósceles $ABC$ es $45^\circ$. Igualando a la mitad del área del triángulo, obtenemos
\[\tfrac{1}{8}\pi r^2=1\ \Longleftrightarrow\ r=2\sqrt{\tfrac{2}{\pi}}.\]
Observamos que $r\lt 2$, lo que nos dice que el sector realmente está bien definido. Ahora bien, el radio $s$ del sector de arco $m$ (en naranja en la figura) sumado con $r$ nos da la hipotenusa $AB=2\sqrt{2}$, luego podemos despejar
\[s=AB-r=2\sqrt{2}-2\sqrt{\tfrac{2}{\pi}}=2\sqrt{2}(1-\tfrac{1}{\sqrt{\pi}}).\]
Tenemos entonces que el área que nos piden (en verde en la figura) es
\[2-\tfrac{\pi}{8}r^2-\tfrac{\pi}{8}s^2=2-1-\tfrac{8\pi}{8}(1-\tfrac{1}{\sqrt{\pi}})^2=2\sqrt{\pi}-\pi.\]
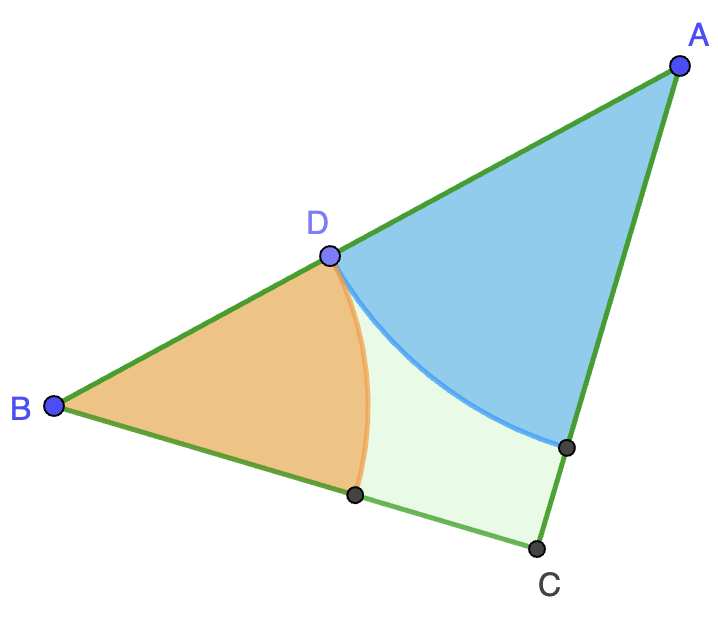
Alrededor de una mesa redonda están sentados representantes de $n$ países ($n\geq 2$), de modo que si dos personas son del mismo país, entonces sus respectivos vecinos de la derecha no son del mismo país. Determinar, para cada $n$, el número máximo de personas que puede haber sentadas en la mesa.
pistasolución 1info
Pista. Usa inducción sobre $n$ para ver que se pueden sentar $n^2$ personas y el principio del palomar para ver que no se pueden sentar más de $n^2$.
Solución. Está claro que no pueden sentarse más de $n^2$ personas cumpliendo esta condición, ya que en tal caso habría al menos $n+1$ de algún país por el principio del palomar y alguna de las personas a su lado tendría que ser del mismo país ya que sólo hay $n$ países (de nuevo por el principio del palomar. Vamos a ver que efectivamente pueden sentarse $n^2$ personas cumpliendo la propiedad, luego este será el máximo.
Vamos a encontrar la forma de sentarse por inducción sobre $n$. Para el caso base $n=2$, la forma de sentarse es 1221 (cíclicamente), siendo 1 un representante del primer país y 2 un representante del segundo. Ahora bien, para añadir un tercer país añadimos 33231 al inicio de la cadena, para añadir un cuarto país añadimos 4434241, para añadir un quinto país añadimos 554535251 y así sucesivamente, obteniendo las cadenas cíclicas
\begin{align*}
1221,\\
332311221,\\
4434241332311221,\\
5545352514434241332311221,\ldots
\end{align*}
En el paso $n$ se añade la cadena $nn(n-1)n(n-2)\ldots n1$ formada por $2n-1$ números. Como la suma de los impares entre $1$ y $2n-1$ es $n^2$, deducimos que tenemos así $n^2$ números para $n$ países. Ahora bien, cada número $k\lt n$ tiene a su derecha a cada uno de los números entre $1$ y $n-1$ una única vez por hipótesis de inducción y una vez al $n$ en la cadena añadida en el paso $n$. Por su parte, el número $n$ tiene a su derecha una vez a cada uno de los números entre $1$ y $n$ en la cadena añadida en el paso $n$. Por lo tanto, hemos probado que el número máximo es $n^2$.
Retos de la semana 12 de 2025
Un número $n$ de siete cifras es bonito si se puede expresar como la
suma de dos números de siete cifras $s$ y $t$ tales que todas las cifras de $s$ son impares y todas las cifras de $t$ son pares. Determinar cuáles de los siguientes números son bonitos:
\[6204773, 6372538, 7343053, 8993267, 9652393.\]
pistasolución 1info
Pista. Si una cifra del número es par es porque hay una llevada en la suma de las cifras de orden inferior. Analiza cada número desde las unidades a las unidades de millón y te darás cuenta de que algunos son imposibles de expresar como $t+s$.
Solución. Hay que tener en cuenta que si una de las cifras del número es par es porque hay una llevada de la suma de las cifras de orden inmediatamente inferior. Vamos a analizar cada caso por separado:
- 6204773 es bonito (por ejemplo, tomando $s=3557931$ y $t=2646842$).
- 6372538 no es bonito puesto que la cifra de las unidades es par y no puede obtenerse como suma de un dígito par y otro impar (no hay llevadas).
- 7343053 no es bonito ya que después del cero de las centenas hay necesariamente una llevada, luego la siguiente cifra no puede ser impar y en este caso es un tres.
- 8993267 no es bonito ya que el 8 en las unidades de millón implica una llevada y por tanto las cifras de $t$ y $s$ en las centenas de millar deben sumar 19, lo que implica que ambas son 9 (más otra llevada de las decenas de millar). Esto impide que las cifras de $s$ sean todas pares.
- 9652393 es bonito (tomando $t=5371751$ y $s=4280642$).
Sea $ABC$ un triángulo acutángulo cuyos lados tienen longitudes $a$, $b$ y $c$ y sea $S$ el área del triángulo. Sea $P$ un punto interior del triángulo de forma que
\[a\cdot PA+b\cdot PB+c\cdot PC=4S.\]
Demostrar que $P$ es el ortocentro del triángulo $ABC$.
pistasolución 1info
Pista. Demuestra que $a\cdot PA+b\cdot PB+c\cdot PC\geq 4S$ para cualquier punto P$ interior, para lo que puede ser útil ver los productos $a\cdot PA$, $b\cdot PB$ y $c\cdot PC$ como áreas. Luego estudia qué tiene que ocurrir para que se alcance la igualdad.
Solución. Trazamos por cada vértice del triángulo una paralela al lado opuesto y definimos los puntos $A',B',C'$ como los pies de las perpendiculares desde $P$ a estas tres rectas, como se muestra en la figura. Tenemos entonces que
\begin{align*}
\mathrm{Area}(ACPB)&=\mathrm{Area}(ABC)-\mathrm{Area}(BPC)=\tfrac{1}{2}a\cdot PA',\\
\mathrm{Area}(CBPA)&=\mathrm{Area}(ABC)-\mathrm{Area}(ABP)=\tfrac{1}{2}b\cdot PB',\\
\mathrm{Area}(BAPC)&=\mathrm{Area}(ABC)-\mathrm{Area}(CPA)=\tfrac{1}{2}c\cdot PC',
\end{align*}
ya que $PA',PB',PC'$ representan la diferencia de alturas de los triángulos cuyas áreas se restan y $a,b,c$ sus bases. Si sumamos las áreas de estos tres cuadriláteros cóncavos, obtenemos dos veces el área de $ABC$, luego esta suma nos da
\[4S=a\cdot PA'+b\cdot PB'+c\cdot PC'.\]
Sin embargo, tenemos que $PA'\leq PA$ ya que $APA'$ es un triángulo rectángulo en el que $PA'$ es un cateto y $PA$ es la hipotenusa. De la misma manera, se cumple que $PB'\leq PB$ y $PC'\leq PC$. En consecuencia,
\[4S\leq a\cdot PA+b\cdot PB+c\cdot PC\]
para cualquier punto $P$ interior al triángulo. Para que la igualdad se alcance, en los triángulos rectángulos $APA'$, $BPB'$ y $CPC'$ tiene que ser $AA'=BB'=CC'=0$, luego $PA=PA'$ es perpendicular a $BC$, $PB=PB'$ es perpendicular a $AC$ y $PC=PC'$ es perpendicular a $AB$. En definitiva, la igualdad se cumple si y sólo si $P$ es está en las tres alturas del triángulo, es decir, sólo si $P$ es el ortocentro.
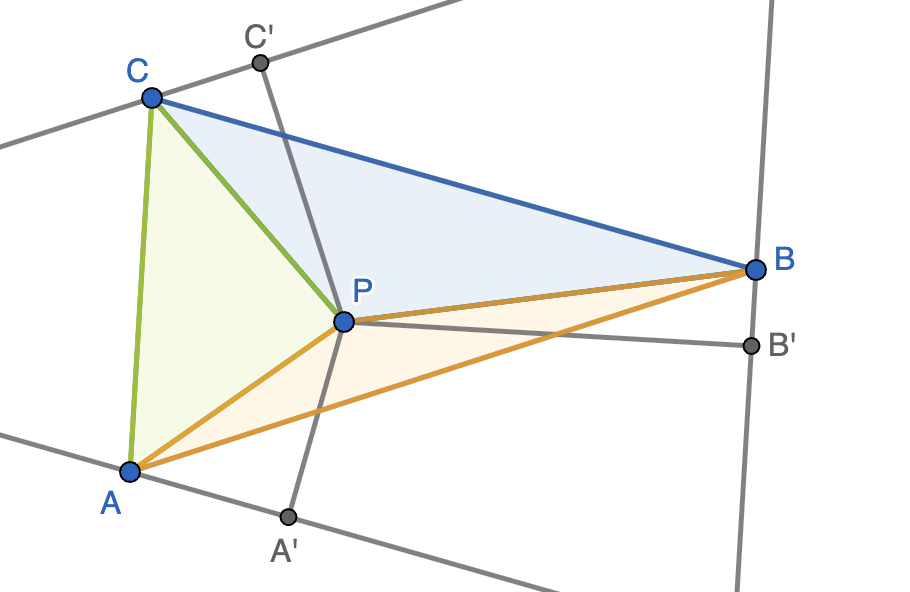
Retos de la semana 11 de 2025
Demuestra que
\[(ax + by)^2\leq ax^2 + by^2\]
para cualesquiera $x,y\in\mathbb{R}$ y cualesquiera $a,b\in\mathbb{R}$ con $a+b=1$, $a,b\geq 0$. ¿En qué casos se da la igualdad?
pistasolución 1solución 2info
Pista. Opera con la desigualdad para transformarla en $ab(x-y)^2\geq 0$ o bien aplica la desigualdad de Jensen.
Solución. Desarrollando los términos, la desigualdad equivale a la siguiente:
\[(a-a^2)x^2-2abxy+(b-b^2)y^2\geq 0.\]
Tenemos ahora que $a-a^2=a(1-a)=ab$ y $b-b^2=b(1-b)=ab$, luego la desigualdad anterior a su vez equivale a la siguiente:
\[abx^2-2abxy+aby^2\geq 0\ \Longleftrightarrow\ ab(x-y)^2\geq 0.\]
Como esta última es obviamente cierta, la primera también lo es. Además, la igualdad se alcanza cuando $a=0$ o $b=0$ o $x=y$.
Solución. No es más que la desigualdad de Jensen para la función estrictamente convexa $f(t)=t^2$ con pesos $a$ y $b$. La igualdad se alcanza cuando uno de los pesos es cero o bien cuando los puntos son iguales, es decir, cuando $a=0$ o $b=0$ o $x=y$.
Sea $a_1,a_2,a_3,\ldots$ una sucesión de números reales positivos. Sabemos que, para algún entero positivo s, se cumple que
\[a_n=\max\{a_k+a_{n-k}:1\leq k\leq n-1\}\]
para todo $n\gt s$. Demostrar que existen enteros positivos $\ell$ y $N$, con $\ell\leq s$, tales que $a_n = a_\ell + a_{n-\ell}$ para todo $n\geq N$.
Sin pistas
Sin soluciones
infoRetos de la semana 10 de 2025
La suma de las edades de los 120 estudiantes que participaron el año pasado en la fase final de la Olimpiada Matemática fue de 2002 años. Demostrar que existen 3 de ellos tales que la suma de sus edades no es menor de 51 años.
pistasolución 1info
Pista. Utiliza el principio del palomar.
Solución. Dividamos a los 120 alumnos en 40 grupos de 3 personas cada uno y supongamos que la suma de las edades de cada grupo es a lo sumo de 50 años. Entonces, todas las edades sumarían como mucho \(40\cdot 50=2000\lt 2002\), lo cual es una contradicción que proviene de lo que se ha supuesto, es decir, hemos probado que habrá un grupo cuya suma de edades sea, al menos, de 51 años.
Un grupo de hombres y mujeres se sienta alrededor de una mesa circular (equidistante cada uno con sus dos vecinos). En total hay $2n$ hombres y $2n$ mujeres. Demostrar que es posible trazar un diámetro de la mesa que divida el grupo en dos partes cada una e las cuales tiene exactamente $n$ hombres y $n$ mujeres.
pistasolución 1info
Pista. ¿Qué ocurre con el número de hombres en un semicírculo de la mesa al ir rotando dicho semicírculo respecto del centro de la mesa?
Solución. Pongamos un diámetro cualquiera que deje a $2n$ personas a un lado y las otras $2n$ personas en otro y supongamos que no hay el mismo número de hombres que de mujeres en los semicírculos así determinados (si los hubiera, habríamos terminado). Rotando este diámetro respecto del centro del círculo, cada vez que sale una persona de uno de los semicírculos entra otra, cambiando el número de hombres en uno de los ellos en $-1$ (si sale un hombre y entra una mujer), $0$ (si sale una persona del mismo género que entra) o $1$ (si entra un hombre y sale una mujer. Cuando el diámetro da media vuelta al círculo, los semicírculos originales se han cambiado uno por el otro, luego, si había $k\gt n$ hombres en uno de ellos, después de la media vuelta hay $2n-k\lt n$ hombres. Como el número de hombres en este semicírculo va variando de uno en uno, necesariamente habrá un diámetro intermedio en el que exactamente haya $n$ hombres en dicho semicírculo (y, por tanto, $2n-n=n$ mujeres) y lo mismo ocurre en el otro semicírculo.
Retos de la semana 9 de 2025
Sea $n$ un número natural. Si la última cifra de $7^n$ es $3$, probar que la
penúltima es $4$.
pistasolución 1info
Pista. Calcula las dos últimas cifras de $7^n$ para $n=0,1,2,3,\ldots$ hasta que encuentres un patrón.
Solución. La última cifra de $7^n$ es $1,7,9,3,1,7,9,3,\ldots$ para $n=0,1,2,3,4,5,6,7,\ldots$ y, como esta sólo depende de la última cifra de $7^{n-1}$, en cuanto una cifra se repite, la sucesión anterior se vuelve periódica. Deducimos así que $7^n$ tiene última cifra $3$ precisamente cuando $n=4k+3$ (ver la nota). Entonces, tenemos que
\[7^{4k+3}=(7^4)^k\cdot 7^3=2401^k\cdot 343\]
tendrá sus dos últimas cifras iguales a $43$ ya que $2041^k$ siempre terminará en $01$ para todo $k$.
Nota. Otra forma de ver la periodicidad de la última cifra es darse cuenta de que $7^4=2041\equiv 1\ (\text{mod }10)$, luego si dividimos $n$ entre $4$ y obtenemos que $n=4k+r$ con $0\leq r\leq 3$, se cumplirá que $7^n=(7^4)^k\cdot 7^r\equiv 1\cdot 7^r\equiv 7^r\ (\text{mod }10)$, luego las últimas cifras se repiten de $4$ en $4$. La solución también se puede terminar con el mismo cálculo observando que, de hecho, $7^4\equiv 1\ (\text{mod }100)$.
Dado un triángulo $OMA$, en los lados $OM$ y $OA$ se construyen cuadrados (en el exterior del triángulo) $OXYM$ y $OAUV$, respectivamente.
- Probar que el segmento $XV$ mide el doble de la mediana trazada desde el vértice $O$.
- Probar que las rectas que contienen a la mediana y al segmento $XV$ son perpendiculares.
pistasolución 1info
Pista. Rota $90^\circ$ el triángulo $OXV$ de forma que $X$ coincida con $M$. Resuelve el problema transformándolo en otro problema en el triángulo $AMV'$, donde $V'$ es el punto rotado de $V$.
Solución. Aplicamos una rotación de $90^\circ$ al triángulo $OXV$ de forma que $X'=M$ (como es usual denotamos con un apóstrofe a los puntos después de aplicarles la rotación). Está claro que se forma un nuevo triángulo $AV'X'$ de forma que $O$ es el punto medio del lado $AV'$. En este triángulo, $O$ es el punto medio del lado $AV'$. Si denotamos por $N$ al punto medio de $AM$, tenemos que $AON$ y $AV'M$ están en posición de Thales y son semejantes con razón de semejanza $\frac{1}{2}$. En particular,
- $XV=X'V'=MV'=2ON$, lo que responde al apartado (a).
- $ON$ es paralela a $X'V'$, luego es perpendicular a $XV$ (que es rotada de $X'V'$ un ángulo recto), lo que responde al apartado (b).
Retos de la semana 8 de 2025
Sea $AD$ la mediana de un triángulo $ABC$ tal que $\angle ADB=45^\circ$ y $\angle ACB = 30^\circ$. Determinar el valor de $\angle BAD$.
pistasolución 1info
Pista. Demuestra que $BAD$ y $ABC$ son triángulos semejantes.
Solución. Llamemos $a,b,c$ a los lados del triángulo como es habitual y $m=AD$ a la mediana. Es bien conocida la fórmula que nos da el valor de $m$ en términos de los lados:
\[m^2=\frac{b^2+c^2}{2}-\frac{a^2}{4}.\]
Ahora bien, en el triángulo $ADC$, tenemos el ángulo $\angle ACD=45^\circ$ y el ángulo $\angle ADC=180^\circ-\angle ADB=135^\circ$, luego el teorema del seno nos dice que
\[\frac{b}{\sen(135)}=\frac{m}{\sen(30)})\ \Longleftrightarrow\ \frac{b}{\frac{\sqrt{2}}{2}}=\frac{m}{\frac{1}{2}}\ \Longleftrightarrow\ m^2=\frac{b^2}{2}.\]
Sustituyendo en la fórmula de la mediana, esto nos da $c^2=\frac{a^2}{2}$, igualdad que se puede escribir como $\frac{a/2}{c}=\frac{c}{a}$, esto es, \frac{BD}{AB}=\frac{AB}{BC}$ y tenemos que los triángulos $ABD$ y $ABC$ son semejantes (tienen un ángulo igual y los lados adyacentes proporcionales). Deducimos así que $\angle BAD=\angle ACB=30^\circ$.
Encontrar la solución entera más pequeña de la ecuación
\[\left\lfloor\frac{x}{8}\right\rfloor+\left\lfloor\frac{x}{40}\right\rfloor+\left\lfloor\frac{x}{240}\right\rfloor=210.\]
Nota. $\lfloor x\rfloor$ denota la parte entera de un número real $x$.
pistasolución 1info
Pista. Escribe $x=240m+40n+8k+r$ con $m,n,k,r$ enteros adecuados dividiendo sucesivamente $x$ entre $240$, el resto entre $40$ y el resto entre $8$.
Solución. Si dividimos $x$ entre $240$, podemos escribir $x=240m+y$ con resto $0\leq y\lt 240$. Dividiendo $y$ entre $40$, podemos escribir $y=40n+z$ con resto $0\leq z\lt 40$. Dividiendo $z$ entre $8$ podemos escribir $z=8k+r$ con resto $0\leq r\lt 8$. Esto nos dice que $x=240m+40n+8k+r$ para ciertos enteros no negativos tales que $y=40n+8k+r\lt 240$, $z=8k+r\lt 40$ y $r\lt 8$, por lo que podemos calcular
\begin{align*}
\left\lfloor\frac{x}{8}\right\rfloor+\left\lfloor\frac{x}{40}\right\rfloor+\left\lfloor\frac{x}{240}\right\rfloor
&=\left\lfloor\tfrac{240m+40n+8k+r}
{8}\right\rfloor+\left\lfloor\tfrac{240m+40n+8k+r}{40}\right\rfloor+\left\lfloor\tfrac{240m+40n+8k+r}{240}\right\rfloor\\
&=\left\lfloor 30m+5n+k+\tfrac{r}
{8}\right\rfloor+\left\lfloor 6m+n+\tfrac{z}{40}\right\rfloor+\left\lfloor m+\tfrac{y}{240}\right\rfloor\\
&=30m+5n+k+6m+n+m=37m+6n+k.
\end{align*}
Tenemos entonces que encontrar la solución de $37m+6n+k=210$ que minimiza $x=240m+40n+8k+r$. Esto nos lleva a elegir directamente $r=0$ ya que $r$ no interviene en la ecuación. Observemos que tenemos la restricción $0\leq n\leq 5$ y $0\leq k\leq 4$, luego $0\leq 6n+k\leq 34$. Así, dividiendo $210$ entre $37$, tenemos $210=5\cdot 37+25$ y deducimos que ha de ser $m=5$, lo que nos deja con $6n+k=25$. La única posible solución positiva con $0\leq k\leq 4$ es $n=4$ y $k=1$. Por tanto, el menor valor posible de $x$ es $240\cdot 5+40\cdot 4+8\cdot 1+0=1368$.
Nota. Esta demostración nos dice que el único grado de libertad que tenemos es $r$ entre $0$ y $7$, luego los únicos $x$ que cumplen esta ecuación son 1368, 1369, 1370, 1371, 1372, 1373, 1374 y 1375.
Retos de la semana 7 de 2025
En el interior de un paralelogramo $ABCD$ se dibujan dos circunferencias. Una es tangente a los lados $AB$ y $AD$ y la otra es tangente a los lados $CD$ y $CB$. Probar que, si estas circunferencias son tangentes entre sí, el punto de tangencia está en la diagonal $AC$.
pistasolución 1info
Pista. Demuestra que los triángulos $AO_1T$ y $CO_2T$ son semejantes, siendo $T$ el punto de tangencia de ambas circunferencias y $O_1$ y $O_2$ sus centros.
Solución. Sean $O_1$ y $r_1$ el centro y el radio de la circunferencia tangente a $AB$ y $AD$ y sean $O_2$ y $r_2$ el centro y el radio de la circunferencia tangente a $CD$ y $CB$. Pongamos también que estas circunferencias son tangentes a $AB$ y $CD$ en los puntos $T_1$ y $T_2$, respectivamente, y que ambas circunferencias son tangentes entre sí en el punto $T$, que está alineado con $O_1$ y $O_2$. Las rectas $AO_1$ y $CO_2$ son paralelas puesto que son las bisectrices del paralelogramo en los vértices opuestos. Estas dos paralelas cortan a la recta $O_1O_2$ formando ángulos alternos internos iguales, es decir, $\angle AO_1T=\angle CO_2T$. Además, los triángulos $AO_1T_1$ y $CO_2T_2$ son triángulos rectángulos semejantes, luego
\[\frac{AO_1}{O_1T}=\frac{AO_1}{O_1T_1}=\frac{CO_2}{O_2T_2}=\frac{CO_2}{O_2T}.\]
Todo esto nos dice que los triángulos $AO_1T$ y $CO_2T$ son semejantes y, en particular, $\angle CTO_2=\angle ATO_1$. Como $O_1$, $O_2$ y $T$ están alineados, esto implica que $T$ está alineado con $A$ y $C$, como queríamos probar.
Determinar un número de cinco cifras tal que su cuadrado termine en las mismas cinco cifras colocadas en el mismo orden.
pistasolución 1info
Pista. Fíjate en que $n^2-n$ debe ser múltiplo de $100000$.
Solución. Si llamamos $n$ al número en cuestión, la condición del enunciado nos dice que $n^2-n=n(n-1)$ debe ser múltiplo de $100000=2^5\cdot 5^5$. Como $n$ y $n-1$ son primos entre sí, uno de ellos debe ser múltiplo de $2^5=32$ y el otro un múltiplo (impar) de $5^5=3125$. Distingamos las dos posibilidades:
- Si $n=3125k$, entonces $n-1=3125k-1\equiv 0\ (\text{mod }32)$, lo cual equivale a que $21k\equiv 1\ (\text{mod }32)$. El inverso de $21$ módulo $32$ es $29$ (¿sabrías calcularlo?), luego tenemos que $k\equiv 29\ (\text{mod }32)$, es decir, $n=3125(32j+29)=100000j+90625$ para cierto entero $j$. Como $n$ debe tener cinco cifras, necesariamente $j=0$ y debe ser $n=90625$.
- Si $n-1=3125k$, entonces $n=3125k+1\equiv 0\ (\text{mod }32)$, luego $21k\equiv -1\ (\text{mod }32)$ y obtenemos $k\equiv -29\equiv 3\ (\text{mod }32)$. Esto nos dice que $n=3125(32j+3)+1=100000j+9376$ para cierto entero $j$, luego debe ser $j=0$ y $n=9376$.
Aunque lo anterior ya nos lo confirma, no está de más comprobar que tanto $n=90625$ como $n=09376$ cumplen la condición del enunciado, aunque habría que descartar el segundo si no lo admitimos como número de $5$ cifras.
Retos de la semana 6 de 2025
El precio de un diamante es proporcional al cuadrado de su peso. Demostrar que, rompiéndolo en dos partes, existe una depreciación de su valor. ¿Cuándo es máxima dicha depreciación?
pistasolución 1info
Pista. Si los trozos pesan $x$ e $y$, tendrás que hallar cuándo $(x+y)^2-x^2-y^2$ es máximo.
Solución. Supongamos que rompemos el diamante de peso $p$ en dos trozos de pesos $x$ e $y$, luego el precio original y el precio tras romperlo son proporcionales a $p^2=(x+y)^2$ y $x^2+y^2$, respectivamente. La depreciación guardará la misma proporción con $(x+y)^2-x^2-y^2=2xy$, luego nos estamos preguntando cuándo será máximo $2xy$ sujetos a la restricción $x+y=p$. De aquí podemos despejar $2xy=2x(p-x)$, con lo que queremos hallar el máximo de la función $f(x)=2x(p-x)$ cuando $0\leq x\leq p$. Esta parábola se anula en $x=0$ y $x=p$, por lo que tendrá su vértice (máximo) en $x=\frac{p}{2}$. Deducimos así que hay romper el diamante en dos partes iguales para que la depreciación sea máxima.
Hallar los valores del número real $a$ para los que todas las raíces del polinomio $p(x)=x^3-2x^2-25x+a$ son números enteros.
pistasolución 1info
Pista. Calcula la suma de los cuadrados de las raíces y mira de qué formas se puede escribir ese número como suma de tres cuadrados.
Solución. Si llamamos $\alpha,\beta,\gamma$ a las tres raíces de $p(x)$, entonces podemos escribir
\begin{align*}
p(x)&=(x-\alpha)(x-\beta)(x-\gamma)\\
&=x^3-(\alpha+\beta+\gamma)x^2+(\alpha\beta+\beta\gamma+\gamma\alpha)x-\alpha\beta\gamma,
\end{align*}
de modo que identificando coeficientes obtenemos las relaciones de Cardano-Vieta:
\[\alpha+\beta+\gamma=2,\qquad \alpha\beta+\beta\gamma+\gamma\alpha=-25,\qquad\alpha\beta\gamma=a.\]
Esto nos permite calcular
\[\alpha^2+\beta^2+\gamma^2=(\alpha+\beta+\gamma)^2-2(\alpha\beta+\beta\gamma+\gamma\alpha)=4+2\cdot 25=54.\]
Las raíces son números enteros y las únicas formas de escribir $54$ como suma de tres cuadrados son $49+4+1$, $36+9+9$ y $25+25+4$. Reordenando las raíces si es necesario, distinguimos tres casos:
- Si $\alpha=\pm 7$, $\beta=\pm 2$ y $\gamma=\pm 1$, es imposible que se cumpla que $\alpha+\beta+\gamma=2$ (el sumando $\alpha=\pm 7$ es demasiado grande en valor absoluto para que sumarle $\beta+\gamma$ lo hagan igual a $2$), luego no hay soluciones en este caso.
- Si $\alpha=\pm 6$, $\beta=\pm 3$ y $\gamma=\pm 3$, también es imposible que se cumpla que $\alpha+\beta+\gamma=2$ ya que $\alpha+\beta+\gamma$ siempre dará un múltiplo de tres independientemente de los signos elegidos.
- Si $\alpha=\pm 5$, $\beta=\pm 5$ y $\gamma=\pm 2$, entonces la condición $\alpha+\beta+\gamma=2$ fuerza a que $\alpha=5$, $\beta=-5$ y $\gamma=2$ (salvo posiblemente intercambiar $\alpha$ y $\beta$). Tenemos entonces que $\alpha\beta\gamma=5\cdot(-5)\cdot 2=-50$, luego $a=50$ único valor que cumple la condición del enunciado.
Retos de la semana 5 de 2025
En cada casilla de un tablero $m\times n$ se encuentra un número real. Se permite cambiar todos los números de una fila o de una columna de signo tantas veces como queramos. Demostrar que puede conseguirse que las sumas de los elementos cada fila y cada columna sean no negativas independientemente de la configuración inicial.
pistasolución 1info
Pista. Analiza la suma total de los elementos cuando cambias de signo una fila o una columna de suma negativa.
Solución. Sea $S$ la suma total de los elementos de la tabla. Cada vez que nos encontremos una fila o columna con suma negativa la cambiamos de signo. Cada una de estas operaciones incrementa el valor de $S$ y, como hay un número limitado de combinaciones de signos (es menor o igual que $2^{mn}$, el número de elecciones de signos $\pm$ en los $mn$ elementos de la tabla), este proceso no puede continuar indefinidamente, es decir, llegamos a un punto en el que todas las filas y columnas tienen suma positiva.
Sea $n\geq 2$ un entero positivo. Tenemos $2n$ bolas, en cada una de las cuales hay escrito un entero. Se cumple que, siempre que formamos $n$ parejas con las bolas, dos de estas parejas tienen la misma suma.
- Demuestra que hay cuatro bolas con el mismo número.
- Demuestra que el número de valores distintos que hay en las bolas es como
mucho $n-1$.
pistasolución 1info
Pista. Busca formas creativas de emparejar según el orden de los valores de forma que la igualdad de dos parejas te dé información útil.
Solución. En el apartado (a), simplemente hay que ordenar las bolas de menor a mayor y luego hacer $n$ parejas de valores consecutivos. Que haya dos sumas iguales implica por tanto que hay cuatro valores $a\leq b\leq c\leq d$ tales que $a+b=c+d$. Esto nos dice que $d=a+b-c\leq a+b-b=a$, luego la anterior cadena de desigualdades nos da $a=b=c=d$.
Para el apartado (b), razonaremos por reducción al absurdo que hay $n$ o más valores distintos. Esto quiere decir que podemos tomar una sucesión estrictamente creciente de valores $x_1\lt x_2\lt\ldots\lt x_n$ y ordenar el resto de valores como $y_1\leq y_2\leq\ldots\leq y_n$. Por lo tanto, se cumple que
\[x_1+y_1\lt x_2+y_2\lt\ldots\lt x_n+y_n,\]
luego si emparejamos cada $x_k$ con el correspondiente $y_k$, ninguna pareja tendrá la misma suma, contradiciendo el enunciado del problema.
Nota. El apartado (b) nos da una estimación óptima. Por ejemplo, podríamos tomar $n-1$ bolas con los valores del $1$ al $n$ y las otras $n+1$ bolas todas iguales a $1$. No importa como emparejemos, siempre habrá dos parejas formadas únicamente por unos y por tanto tendrán la misma suma.
Retos de la semana 4 de 2025
De entre los triángulos que tienen un lado de $5$ m de longitud y el ángulo opuesto de $30^\circ$, determinar el de área máxima, calculando el valor de los otros dos ángulos y el área del triángulo.
pistasolución 1info
Pista. Fijando el lado de $5$ m como base, encuentra el que tiene altura máxima.
Solución. Si fijamos el lado $AB=5$ como base, el vértice opuesto $C$ tiene que estar sobre el arco mayor de la circunferencia que fija pasa por $A$ y $B$ formada por los puntos del plano que ven $AB$ bajo un ángulo de $30^\circ$ (propiedad del arco capaz). Si $h$ es la altura sobre el lado $AB$, entonces el área será máxima cuando $h$ sea máxima, lo que nos dice claramente que $C$ debe ser el punto más alejado del arco y, por tanto, estará sobre la mediatriz de $AB$, esto es, el triángulo $ABC$ será isósceles y tendrá ángulos de $75^\circ$ en $A$ y $B$. Usando razones trigonométricas en el triángulo rectángulo $ACM$, siendo $M$ el punto medio de $AB$, tenemos que
\[h=\tfrac{5}{2}\tan(75^\circ)=\tfrac{5}{2}(2+\sqrt{3})\]
(¿sabrías demostrar que $\tan(75^\circ)=2+\sqrt{3}$?), luego el área estará dada por
\[S=\tfrac{1}{2}AB\cdot h=\tfrac{25}{4}(2+\sqrt{3}).\]
Decimos que un número natural $n$ es
charrúa si satisface simultáneamente las siguientes condiciones:
- Todos los dígitos de $n$ son mayores que $1$.
- Siempre que se multipliquen cuatro dígitos de $n$ se obtiene un divisor de $n$.
Demostrar que para cada número natural $k$ existe un número charrúa con más de $k$ dígitos.
pistasolución 1info
Pista. Usar números formados únicamente por nueves.
Solución. Como $10$ es primo relativo con $9^4$, el teorema de Euler nos asegura que $n=\varphi(9^4)=\varphi(3^8)=2\cdot 3^7$ verifica que $10^n\equiv 1\ (\mathrm{mod}\ 9^4)$. Entonces, $10^n-1$ es un número formado únicamente por nueves que es múltiplo de $9^4$, luego es charrúa. También es charrúa el número $10^{bn}-1$ para todo entero positivo $b$ ya que $10^{bn}=(10^{n})^b\equiv 1^b=1\ (\mathrm{mod}\ 9^4)$. Como $10^{bn}-1$ tiene $bn$ dígitos, obtenemos de este modo números charrúas con tantos dígitos como queramos.
Nota. Hemos usado la función de Euler $\varphi(n)$ que devuelve el número de enteros entre $1$ y $n$ que son primos relativos con $n$.
Retos de la semana 3 de 2025
Hallar todas las aplicaciones $f:\mathbb{Z}\to\mathbb{Z}$ que verifican
\[f(n)+f(n+1)=2n+1\]
para cualquier entero $n$ y además $f(1)+f(2)+\ldots+f(63)=2015$.
pistasolución 1info
Pista. Observa que $f(n)$ está determinada por el valor de $f(0)$.
Solución. Cambiando $n$ por $n+1$ obtenemos la igualdad $f(n+1)+f(n+2)=2n+3$. Si a esta le restamos la ecuación del enunciado, obtenemos que $f(n+2)=f(n)+2$ para todo entero $n$. De aquí se deduce fácilmente por inducción sobre $k$ que
\[f(2k)=2k+f(0),\qquad f(2k+1)=2k+f(1).\]
Por tanto, $a=f(0)$ y $b=f(1)$ determinan completamente a la función y verifican $a+b=1$ (haciendo $n=0$ en la ecuación funcional original). Si imponemos la otra condición del enunciado, tenemos que
\begin{align*}
2015&=f(1)+f(2)+\ldots+f(63)\\
&=31a+2+4+\ldots+62+32b+2+4+\ldots+62\\
&=31a+32b+2(1+2+\ldots+31)=31a+32b+31\cdot 32=31a+32b+992.
\end{align*}
Por tanto, tenemos el sistema de ecuaciones
\[\left\{\begin{array}{l}a+b=1\\31a+32b=1023\end{array}\right.\]
que se resuelve fácilmente dando la solución única $a=-991$ y $b=992$. Deducimos así que solo existe una función cumpliendo las condiciones dadas y está definida por
\[f(n)=\begin{cases}n-991&\text{si }n\text{ par},\\n+991&\text{si }n\text{ impar}.\end{cases}\]
El ángulo $A$ del triángulo isósceles $ABC$ mide $36^\circ$, siendo iguales sus ángulos $B$ y $C$. La bisectriz de su ángulo $C$ corta al lado opuesto en el punto $D$.
- Calcular las medidas de los ángulos del triángulo $BCD$.
- Expresar la medida del lado $BC$ en función de la medida del lado $AC$, sin que en la expresión aparezcan razones trigonométricas.
pistasolución 1info
Pista. Busca un triángulo semejante a $ABC$ en la figura que resulta al trazar las diagonales de un pentágono regular.
Solución. Por ser el triángulo isósceles, tenemos que $\angle ABC=\angle ACB=\frac{180-36}{2}=72^\circ$. La bisectriz divide al ángulo en dos ángulos iguales, luego $\angle ABD=\angle DBC=\frac{72}{2}=36^\circ$. Además, como la suma de los ángulos de $BCD$ es $180^\circ$, obtenemos rápidamente $\angle BDC=180-36-72=72$. Por tanto, el triángulo $BCD$ es isósceles y tiene ángulos de $36^\circ, 72^\circ, 72^\circ$ (véase la figura).
El triángulo $ABD$ también es isósceles por tener dos ángulos iguales a $36^\circ$, luego $BC=BD=AD$. Además, $BCD$ y $ABC$ son semejantes por tener los ángulos iguales, luego
\[\frac{AC}{BC}=\frac{BC}{CD}=\frac{BC}{AC-AD}=\frac{BC}{AC-BC}.\]
De esta igualdad, obtenemos que $AC^2-AC\cdot BC-BC^2=0$. Dividiendo entre $AC^2$, llegamos a la ecuación de segundo grado
\[\left(\frac{BC}{AC}\right)^2+\frac{BC}{AC}-1=0\ \Longrightarrow\ \frac{BC}{AC}=\frac{-1\pm\sqrt{5}}{2}.\]
Tenemos que descartar la solución negativa, lo que nos dice finalmente que
\[BC=\frac{\sqrt{5}-1}{2}AC.\]
Retos de la semana 2 de 2025
Dos jugadores $A$ y $B$ y otras $2001$ personas forman un círculo, de modo que $A$ y $B$ no quedan en posiciones consecutivas. $A$ y $B$ juegan por turnos alternadamente empezando por $A$. Una jugada consiste en tocar a una de las personas que se encuentran a su lado, la cual debe salir del círculo. Gana el jugador que logre sacar del círculo a su oponente. Demostrar que uno
de los dos jugadores tiene una estrategia ganadora y describir dicha estrategia.
pistasolución 1info
Pista. Observa la paridad de personas que quedan en cada uno de los dos arcos de circunferencia de extremos $A$ y $B$.
Solución. Como hay un número impar de jugadores, en uno de los dos arcos de extremos $A$ y $B$ habrá un número par de personas y en el otro un número impar. El primer jugador tiene una estrategia ganadora que consiste en eliminar primero una persona del arco que tiene un número par para dejar los dos con una cantidad impar de personas. A partir de ahí, $A$ sólo tiene que copiar el arco que ha elegido $B$ en su turno. Esto le garantiza que siempre queda un número impar de personas en cada arco tras su jugada; en particular, no quedan cero personas y $B$ no puede ganar en su turno siguiente. El primer jugador que deja un arco con ninguna persona es $B$ y en su siguiente turno $A$ lo elimina.
Un jardinero tiene que plantar en una fila a lo largo de un camino tres
robles, cuatro encinas y cinco hayas. Planta los árboles al azar siendo la
probabilidad de plantar un árbol u otro la misma. Halla la probabilidad de que, una vez plantados todos los árboles, no haya dos hayas consecutivas.
pistasolución 1info
Pista. Para contar los casos favorables, impón que haya cuatro árboles que no sean hayas entre las 5 hayas y luego coloca los otros tres árboles libremente.
Solución. Para centrar el problema, vamos a pensar que el jardinero tiene los 12 árboles en macetas y va cogiendo una a una una maceta sin mirar de qué tipo de árbol es y la planta consecutivamente en 12 agujeros que previamente ha cavado. De esta forma, está claro que hay $12!$ formas posibles de plantar los árboles. Veamos cuántas de ellas tienen no tienen hayas consecutivas para hallar la probabilidad como
casos favorables entre casos posibles
.
Denotamos por $H$ a las hayas y por $A$ a los otros árboles (robles o encinas). Para que no estén consecutivas, tendremos que poner al menos un árbol entre cada haya:
\[\_\ H\ A\ \_\ H\ A\ \_\ H\ A\ \_\ H\ A\ \_\ H\ \_\]
aunque nos quden seis huecos marcados con $\_$ para poner otras tres $A$. Estas se podrán poner libremente en uno de los seis huecos, lo que nos da un total de $6^3$ configuraciones. Para cada una de ellas, podemos permutar las $H$ y permutar las $A$ libremente, lo que nos da un total de $5!\cdot 7!$ casos posibles por cada una de las $6^3$ configuraciones. La probabilidad que buscamos es, por lo tanto,
\[\frac{6^3\cdot 5!\cdot 7!}{12!}=\frac{3}{11}.\]
Retos de la semana 1 de 2025
Hallar todos los números enteros positivos que son menores que $1000$ y que cumplen que el cubo de la suma de sus cifras es igual al cuadrado del dicho entero.
pistasolución 1info
Pista. Observa que el número tiene que ser un cubo perfecto y, entre $1$ y $999$, no hay tantos cubos perfectos.
Solución. Un número que cumpla dicha condición cumple que su cuadrado es un cubo perfecto luego el número en sí ha de ser un cubo perfecto (todos los exponentes en su descomposición de su cuadrado en factores primos han de ser múltiplos de $3$ luego los del propio número también). Como tiene que ser menor que $1000$, tenemos las posibilidades $1$, $8$, $27$, $64$, $125$, $216$, $343$, $512$ y $729$. Además, por el mismo motivo, la suma de sus cifras ha de ser un cuadrado perfecto luego de estos nos quedan $1$, $27$ y $216$, de los cuales sólo $1$ y $27$ cumplen la condición buscada.
Tenemos $n$ puntos en el plano, algunos de los cuales están conectados por segmentos que no se cortan entre sí. Sabemos además que se puede viajar entre cualesquiera dos puntos moviéndonos a lo largo de los segmentos y sólo hay una forma de viajar entre dichos puntos. Demostrar que el número total de segmentos es $n-1$.
pistasolución 1info
Pista. Hacer inducción sobre $n$.
Solución. Procedamos por inducción sobre $n$. El caso base es $n=2$, en cuyo caso hay necesariamente dos puntos unidos por $n-1=1$ segmentos y no hay nada que probar. Supongamos entonces que el enunciado es cierto tal cual está escrito para $n$ puntos y veamos lo que pasa si tenemos $n+1$ puntos con dicha propiedad. Al hacer un camino a lo largo de los segmentos sin repetir segmento, como no podemos volver a ningún punto ya visitado (habría dos caminos distintos con el mismo origen y el mismo final), llegará un momento en que no podremos seguir y habremos alcanzado un punto $p_0$ al que solo llega un segmento (mediante el cual hemos accedido a $p_0$). Si eliminamos $p_0$ y dicho segmento, tendremos $n$ puntos que verifican la misma propiedad, luego la hipótesis de inducción nos asegura que el número de segmentos es $n-1$. Añadiendo el que hemos eliminado, deducimos que el número de segmentos para $n+1$ puntos es $n$, como queríamos probar.


















