Listado de problemas de preparación anteriores
Problema 40 (nivel 1) (propuesto el 1-4-2024) Para cada entero positivo \(n\), determinar si existe una circunferencia en el plano que no pasa por ningún punto de coordenadas enteras pero en cuyo interior hay exactamente \(n\) puntos de coordenadas enteras.
SoluciónSolución. Consideremos el punto \(C=(\sqrt{2},\sqrt{3})\). Veamos, por reducción al absurdo, que no hay dos puntos distintos de coordenadas enteras que equidisten de \(C\). En efecto, si \((x_1,y_1)\) y \((x_2,y_2)\) fueran tales puntos, tendríamos que \[(x_1-\sqrt{2})^2+(y_1-\sqrt{3})^2=(x_2-\sqrt{2})^2+(y_2-\sqrt{3})^2.\] Desarrollando los cuadrados en esta igualdad, tenemos equivalentemente que \[2(x_2-x_1)\sqrt{2}+2(y_2-y_1)\sqrt{3}=x_2^2-x_1^2+y_2^2-y_1^2.\] Esto nos da una combinación de \(\sqrt{2}\) y \(\sqrt{3}\) con coeficientes enteros igual a otro número entero, lo cual solo es posible si dichos coeficientes son cero, de donde deducimos que \(x_1=y_1\) y \(x_2=y_2\), en contra de que hemos supuesto que los puntos \((x_1,y_1)\) y \((x_2,y_2)\) son distintos.
Esto nos lleva a que las circunferencias de centro \(C\) al aumentar el radio de \(0\) a \(+\infty\) van encontrando los puntos de coordenadas enteras de uno en uno. Por ello, deducimos que es posible encontrar circunferencias en cuyo interior hay cualquier número \(n\geq 0\) de puntos de coordenadas enteras.
Problema 39 (nivel 1) (propuesto el 1-4-2024) Sea \(p\) el perímetro de un triángulo \(ABC\) y \(P\) un punto interior al triángulo. Demostrar que \[\frac{p}{2}\leq AP+BP+CP\leq p.\]
SoluciónSolución. Aplicando la desigualdad triangular a los triángulos \(ABP\), \(BCP\) y \(ACP\), obtenemos las desigualdades: \begin{align*}AP+BP&\leq AB,\\BP+CP&\leq BC,\\CP+AP&\leq AC.&\end{align*} Sumando las tres llegamos a que \(AP+BP+CP\geq\frac{p}{2}\).
Para probar la otra desigualdad, prolongamos \(AP\) hasta un punto \(Q\) en \(BC\). La desigualdad triangular en el triángulo \(BPQ\) nos dice que \(BP\leq PQ+BQ\) y en el triángulo \(ACQ\) también nos dice que \(AQ\leq AC+QC\). Entonces, podemos escribir $$AP+BP\leq AP+PQ+BQ=AQ+BQ\leq AC+QC+BQ=AC+BC.$$ De la misma forma, se prueba que \(AP+CP\leq AB+BC\) y \(BP+CP\leq AB+AC\). Sumando estas tres desigualdades, llegamos a que \(AP+BP+CP\leq p\).
Problema 38 (nivel 2) (propuesto el 25-3-2024) Consideramos el polinomio \[p(x)=(x-a)(x-b)+(x-b)(x-c)+(x-c)(x-a).\] Demostrar que \(p(x)\geq 0\) para todo \(x\in\mathbb{R}\) si, y solamente si, \(a=b=c\).
SoluciónSolución. Hay que probar dos implicaciones. La más sencilla consiste en suponer que \(a=b=c\), en cuyo caso para cualquier \(x\in\mathbb{R}\) se cumple que \[p(x)=(x-a)(x-b)+(x-b)(x-c)+(x-c)(x-a)=3(x-a)^2\geq 0.\] Recíprocamente, supongamos que \(p(x)\geq 0\) para todo \(x\in\mathbb{R}\). Podemos simplificar el polinomio operando todos los paréntesis y luego completar cuadrados para obtener que\begin{align*}p(x)&=x^2-ax-bx+ab+x^2-bx-cx+bc+x^2-cx-ax+ca\\&=3x^2-2(a+b+c)x+(ab+bc+ca)\\&=3\left(x^2-\tfrac{1}{3}(a+b+c)\right)^2-\tfrac{1}{3}(a+b+c)^2+(ab+bc+ca).\end{align*}Por tanto, este polinomio toma su mínimo valor en \(x=\frac{1}{3}(a+b+c)\) y esto nos dice que \p(\frac{1}{3}(a+b+c))\geq 0\). De esta manera\begin{align*} 0\leq 3\, p(\tfrac{1}{3}(a+b+c))&=-(a+b+c)^2+3(ab+bc+ca)\\&=-(a^2+b^2+c^2)-2(ab+bc+ac)+3(ab+bc+ca)\\&=-(a^2+b^2+c^2)+(ab+bc+ac)\\&=-(a-b)^2-(b-c)^2-(c-a)^2.\end{align*}La única forma de que se cumpla esta desigualdad es que \(a-b=b-c=c-a=0\), es decir, que \(a=b=c\), como queríamos demostrar.
Este fue el problema número 4 en la fase local de la Olimpiada Matemática Española de 2020.
Problema 37 (nivel 1) (propuesto el 25-3-2024) ¿Existe algún número entero mayor que \(10\) que sea un cuadrado perfecto y además tenga todas sus cifras iguales?
SoluciónSolución. Supongamos que \(n\) es un cuadrado perfecto con todas sus cifras iguales y llamemos \(a\) a la cifra de las unidades de \(n\). Por un lado, si \(n\) tiene todas sus cifras iguales, entonces \(n=ab\) siendo \(b\) un número formado sólo por unos. Por otro lado, los únicos valores posibles de \(a\) son \(0\), \(1\), \(4\), \(5\), \(6\) y \(9\) (ya que depende sólo de la cifra de las unidades del número del que \(n\) es cuadrado).
- No puede ser \(a=0\) porque entonces sería \(n=0\cdot b=0<10\).
- No puede ser \(a=5\) porque entonces \(b\) tendría otro factor \(5\), pero claramente \(b\) no es múltiplo de \(5\).
- No puede ser \(a=6\) por la misma razón (\(b\) tendría otro factor \(2\) pero no es un número par).
En el resto de casos \(a=1\), \(a=4\) y \(a=9\), el propio \(a\) es un cuadrado perfecto, luego tendremos que ver que el número \(b\) formado sólo por unos no lo es. Por reducción al absurdo, si \(b=m^2\) fuera un cuadrado perfecto, entonces la cifra de las unidades de \(m\) será \(1\) o \(9\), luego \(m=10k+1\) o bien \(m=10k+9\) para cierto \(k\geq 1\). Elevando al cuadrado tenemos que \[b=(10k+1)^2=100k^2+20k+1=20(5k^2+k)+1,\] luego \(b\) es un múltiplo de \(20\) más \(1\), es decir, la cifra de las decenas de \(b\) es par, lo que contradice que \(b\) está formado sólo por unos. De la misma forma, \[(10k+9)^2=100k^2+180k+81=20(5k^2+9k+4)+1\] no puede estar formado sólo por unos.
Este fue el problema número 2 en el concurso Retos Matemáticos en la UJA de 2021.
Problema 36 (nivel 1) (propuesto el 18-3-2024) Hallar todos los números naturales \(n\) que verifican la condición: \[\biggl\lfloor\frac{n}{2}\biggr\rfloor+\biggl\lfloor\frac{2n}{3}\biggr\rfloor =n+335.\]
Nota. \(\lfloor x\rfloor\) denota la parte entera de un número real \(x\).
SoluciónSolución. Distinguimos casos según el resto de dividir \(n\) entre \(6\).
- Si \(n=6k\), entonces \(\lfloor\frac{n}{2}\rfloor=\lfloor 3k\rfloor=3k\) y \(\lfloor\frac{2n}{3}\rfloor=\lfloor 4k\rfloor=4k\), luego la ecuación queda \(7k=6k+335\), cuya solución es \(k=335\). Tenemos así que \(n=6\cdot 335=2010\).
- Si \(n=6k+1\), entonces \(\lfloor\frac{n}{2}\rfloor=\lfloor 3k+\frac{1}{2}\rfloor=3k\) y \(\lfloor\frac{2n}{3}\rfloor=\lfloor 4k+\frac{2}{3}\rfloor=4k\), luego la ecuación queda \(7k=6k+336\), cuya solución es \(k=336\). Tenemos así que \(n=6\cdot 336+1=2017\).
- Si \(n=6k+2\), entonces \(\lfloor\frac{n}{2}\rfloor=\lfloor 3k+1\rfloor=3k+1\) y \(\lfloor\frac{2n}{3}\rfloor=\lfloor 4k+\frac{4}{3}\rfloor=4k+1\). La ecuación queda \(7k+2=6k+337\), luego \(k=335\) y \(n=6\cdot 335+2=2012\).
- Si \(n=6k+3\), entonces \(\lfloor\frac{n}{2}\rfloor=\lfloor 3k+\frac{3}{2}\rfloor=3k+1\) y \(\lfloor\frac{2n}{3}\rfloor=\lfloor 4k+2\rfloor=4k+2\). La ecuación queda \(7k+3=6k+338\), luego \(k=335\) y \(n=6\cdot 335+3=2013\).
- Si \(n=6k+4\), entonces \(\lfloor\frac{n}{2}\rfloor=\lfloor 3k+2\rfloor=3k+2\) y \(\lfloor\frac{2n}{3}\rfloor=\lfloor 4k+\frac{8}{3}\rfloor=4k+2\). La ecuación queda \(7k+4=6k+339\), luego \(k=335\) y \(n=6\cdot 335+4=2014\).
- Si \(n=6k+5\), entonces \(\lfloor\frac{n}{2}\rfloor=\lfloor 3k+\frac{5}{2}\rfloor=3k+2\) y \(\lfloor\frac{2n}{3}\rfloor=\lfloor 4k+\frac{10}{3}\rfloor=4k+3\). La ecuación queda \(7k+5=6k+340\), luego \(k=335\) y \(n=6\cdot 335+5=2015\).
Deducimos así que las soluciones son 2010, 2012, 2013, 2014, 2015 y 2017.
Este fue el problema 3 de la fase local de la Olimpiada Matemática Española de 2010.
Problema 35 (nivel 1) (propuesto el 18-3-2024) En una fila hay 2022 personas. Cada una de ellas o siempre miente o siempre dice la verdad. Todos ellos afirman
hay más mentirosos a mi izquierda que personas que digan la verdad a mi derecha
. Determinar cuántos mentirosos hay en la fila.
SoluciónSolución. Todas las personas no pueden ser mentirosas, ya que entonces la que está más a la derecha estaría diciendo la verdad. Tampoco pueden decir todas la verdad ya que entonces la que está más a la izquierda sería mentirosa. En particular, tenemos que la que está más a la derecha debe decir la verdad y la que está más a la izquierda es mentirosa. Si ahora a estas dos las quitamos de la fila, quedarán otras 2020 personas. Al haber quitado una mentirosa a la izquierda de todas y una sincera a la derecha, la afirmación de que
hay más mentirosos a mi izquierda que personas que digan la verdad a mi derecha
sigue teniendo la misma validez si solo miramos a estas 2020 personas. El mismo razonamiento nos permite reducir el problema de 2020 a 2018, de 2018 a 2016 y así sucesivamente, luego las 1011 personas más a la izquierda mienten y las 1011 más a la derecha son sinceras.
Este fue el problema 5 de la fase local de la Olimpiada Matemática Española de 2022.
Problema 34 (nivel 2) (propuesto el 11-3-2024) Sean \(a,b,c\) números reales tales que \(a^2+b^2+c^2=1\). Hallar los valores máximo y mínimo posibles de \(ab+bc+ac\).
SoluciónSolución. En primer lugar, tenemos que\[2(ab+bc+ac)=(a+b+c)^2-(a^2+b^2+c^2)=(a+b+c)^2-1\geq -1\] y de aquí deducimos que \(ab+bc+ac\leq \frac{-1}{2}\). Por otro lado, podemos usar las desigualdades \(ab\leq\frac{1}{2}(a^2+b^2)\), \(bc\leq\frac{1}{2}(b^2+c^2)\) y \(ac\leq\frac{1}{2}(a^2+c^2)\), que nos dicen directamente que \(ab+bc+ac\leq a^2+b^2+c^2=1\).
La igualdad \(ab+bc+ac=1\) se tiene obviamente cuando \(a+b+c=0\) y \(ab+bc+ac= \frac{-1}{2}\) cuando \(a=b=c=\frac{\sqrt{3}}{3}\), luego el valor mínimo es \(\frac{-1}{2}\) y el valor máximo \(1\).
Problema 33 (nivel 2) (propuesto el 11-3-2024) Sean \(\alpha\), \(\beta\) y \(\gamma\) los ángulos de un triángulo. Demostrar que \[\sin(\alpha)+\sin(\beta)+\sin(\gamma)\leq\frac{3\sqrt{3}}{2}.\]Analizar en qué casos se obtiene una igualdad.
SoluciónSolución. La función seno es cóncava en el intervalo \([0,\pi]\), intervalo en donde se mueven los ángulos de un triángulo, por lo que la desigualdad de Jensen nos asegura que \[\frac{\sin(\alpha)+\sin(\beta)+\sin(\gamma)}{3}\leq\sin\left(\frac{\alpha+\beta+\gamma}{3}\right)=\sin(60º)=\frac{\sqrt{3}}{2}.\] Como la función es estrictamente convexa (su gráfica no contiene segmentos rectilíneos), deducimos que la igualdad se alcanza cuando \(\alpha=\beta=\gamma\), es decir, cuando el triángulo es equilátero.
Problema 32 (nivel 3) (propuesto el 4-3-2024) Sea \(ABCD\) un cuadrilátero convexo y sea \(P\) un punto en el interior. Si se cumple que \[\text{Área}(PAB)\cdot\text{Área}(PCD)=\text{Área}(PBC)\cdot\text{Área}(PDA),\] demostrar que \(P\) se encuentra en el segmento \(AC\) o en el segmento \(BD\).
SoluciónSolución. Consideremos los ángulos \(\alpha=\angle APB\), \(\beta=\angle BPC\), \(\gamma=\angle CPD\) y \(\delta=\angle DPA\), que suman \(360^\circ\). Entonces, podemos escribir \begin{align*} \text{Área}(PAB)&=\tfrac{1}{2}PA\cdot PB\cdot\mathrm{sen}(\alpha),& \text{Área}(PCD&)=\tfrac{1}{2}PC\cdot PD\cdot\mathrm{sen}(\gamma),\\ \text{Área}(PBC)&=\tfrac{1}{2}PB\cdot PC\cdot\mathrm{sen}(\beta),& \text{Área}(PDA&)=\tfrac{1}{2}PD\cdot PA\cdot\mathrm{sen}(\delta).\end{align*}Por tanto, la condición del enunciado se escribe como\[\mathrm{sen}(\alpha)\mathrm{sen}(\gamma)=\mathrm{sen}(\beta)\mathrm{sen}(\delta).\qquad (\star)\]Ahora bien, como \(\alpha+\beta+\gamma+\delta=360^\circ\), la igualdad \((\star)\) nos dice que\begin{align*}\cos(\alpha+\gamma)=\cos(\beta+\delta)&\ \Leftrightarrow\ \cos(\alpha)\cos(\gamma)-\mathrm{sen}(\alpha)\mathrm{sen}(\gamma)=\cos(\beta)\cos(\delta)-\mathrm{sen}(\beta)\mathrm{sen}(\delta)\\&\ \Leftrightarrow\ \cos(\alpha)\cos(\gamma)=\cos(\beta)\cos(\delta).\end{align*}Elevando esta última al cuadrado y cambiando \(\cos^2=1-\mathrm{sen}^2\), llegamos a que \[(1-\mathrm{sen}^2(\alpha))(1-\mathrm{sen}^2(\gamma))=(1-\mathrm{sen}^2(\beta))(1-\mathrm{sen}^2(\delta)).\] Desarrollamos y usamos \((\star)\) de nuevo para obtener que \[\mathrm{sen}^2(\alpha)+\mathrm{sen}^2(\gamma)=\mathrm{sen}^2(\beta)+\mathrm{sen}^2(\delta)\] Sumando dos veces \((\star)\) a esta última ecuación, nos queda \[\left(\mathrm{sen}(\alpha)+\mathrm{sen}(\gamma)\right)^2=\left(\mathrm{sen}(\beta)+\mathrm{sen}(\delta)\right)^2.\]Como todos los senos son positivos (aquí usamos que el cuadrilátero es convexo, luego \(\alpha,\beta,\gamma,\delta\lt 180^\circ\)), deducimos finalmente que \(\mathrm{sen}(\alpha)+\mathrm{sen}(\gamma)=\mathrm{sen}(\beta)+\mathrm{sen}(\delta)\). En otras palabras, las dos parejas \((\mathrm{sen}(\alpha),\mathrm{sen}(\gamma))\) y \((\mathrm{sen}(\beta),\mathrm{sen}(\delta))\) tienen la misma suma y el mismo producto, luego son iguales salvo reordenación.
- Si \(\mathrm{sen}(\alpha)=\mathrm{sen}(\beta)\) y \(\mathrm{sen}(\gamma)=\mathrm{sen}(\delta)\), hay dos posibilidades. La primera es que \(\alpha+\beta=180^\circ\) o \(\beta+\delta=180^\circ\) (en cuyo caso, \(P\) está en la diagonal \(AC\) o \(BD\), respectivamente). La segunda es que \(\alpha=\beta\) y \(\gamma=\delta\); como \(\alpha+\beta+\gamma+\delta=360^\circ\), se tiene que \(\alpha+\delta=180^\circ\) y \(P\) está sobre \(BD\).
- Si \(\mathrm{sen}(\alpha)=\mathrm{sen}(\delta)\) y \(\mathrm{sen}(\gamma)=\mathrm{sen}(\beta)\), se razona de forma totalmente análoga.
Este fue el problema 6 de la fase local de la Olimpiada Matemática Española de 2022.
Problema 31 (nivel 2) (propuesto el 4-3-2024) Hallar todas las ternas de números reales \((a,b,c)\) que cumplen el sistema \[\left\{\begin{array}{l}a+b+c=3,\\2^a+2^b+2^c=7,\\2^{-a}+2^{-b}=\frac{3}{4}.\end{array}\right.\]
SoluciónSolución. Llamamos \(x=2^a\) e \(y=2^b\) por comodidad. Podemos eliminar \(c\) en la segunda ecuación usando la primera para escribir\[7=2^a+2^b+2^{3-a-b}=2^a+2^b+\frac{8}{2^a2^b}=x+y+\frac{8}{xy}.\]Por otro lado, la tercera ecuación nos dice que \(\frac{1}{x}+\frac{1}{y}=\frac{3}{4}\), que también puede escribirse como \(x+y=\frac{3}{4}xy\). Por tanto, tenemos que \[7=x+y+\frac{8}{xy}=\frac{3}{4}xy+\frac{8}{xy}\ \Leftrightarrow\ 3(xy)^2-28xy+32=0.\] Esto puede verse como una ecuación de segundo grado con incógnita el producto \(xy\), que nos da las soluciones \(xy=\frac{4}{3}\) y \(xy=8\). Distingamos los dos casos:
- Si \(xy=\frac{4}{3}\), entonces \(x+y=\frac{3}{4}xy=1\). Conociendo la suma \(1\) y el producto \(\frac{3}{4}\), ls números \(x\) e \(y\) deben las soluciones de la ecuación \)t^2-t+\frac{3}{4}=0\), pero esta ecuación no tiene soluciones reales.
- Si \(xy=8\), entonces \(x+y=\frac{3}{4}xy=6\), en cuyo caso \(x\) e \(y\) son soluciones de la ecuación \(t^2-6t+8=0\), que son \(t=2\) y \(t=4\), lo que nos da \(a=1\) y \(b=2\) (salvo reordenación) y la condición \(a+b+c=3\) nos da \(c=0\).
Deducimos así que las soluciones al sistema son \((1,2,0)\) y \((2,1,0)\).
Este fue el problema 7 de la fase local de la Olimpiada Matemática Española de 2022.
Problema 30 (nivel 1) (propuesto el 26-2-2024) Sean \(x,y,z\) números reales positivos.
- Si \(x+y+z\geq 3\), ¿se verifica necesariamente que \(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\leq 3\)?
- Si \(x+y+z\leq 3\), ¿se verifica necesariamente que \(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\geq 3\)?
SoluciónSolución. La respuesta al apartado (a) es negativa. Por ejemplo, los números \(x=1\), \(y=\frac{1}{2}\) y \(z=\frac{3}{2}\) cumplen \(x+y+z=3\), pero \(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=\frac{11}{3}\gt 3\).
La respuesta al apartado (b) es afirmativa. Para verlo, usamos la desigualdad entre las medias aritmética y armónica aplicada a los tres números positivos \(x,y,z\):\[\frac{3}{\frac{1}{x}+\frac{1}{y}+\frac{1}{z}}\leq \frac{x+y+z}{3}\leq 1\ \Longleftrightarrow\ \frac{1}{x}+\frac{1}{y}+\frac{1}{z}\geq 3.\]
Este fue el problema 3 de la fase local de la Olimpiada Matemática Española de 2005.
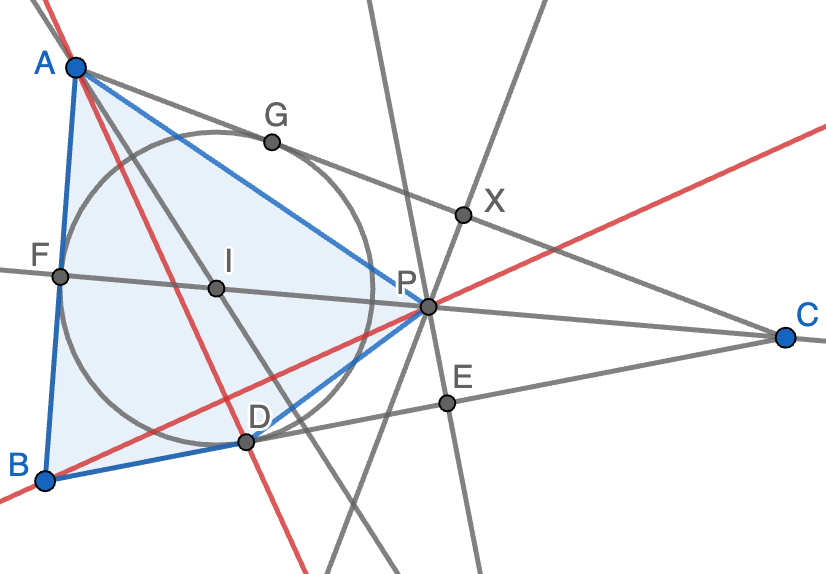
Problema 29 (nivel 2) (propuesto el 26-2-2024) Sea \(ABC\) un triángulo con \(AB\lt AC\) y sea \(I\) su incentro. La circunferencia inscrita en \(ABC\) es tangente al lado \(BC\) en el punto \(D\). Sea \(E\) el único punto que satisface que \(D\) es el punto medio del segmento \(BE\). La línea perpendicular a \(BC\) que pasa por \(E\) corta a \(CI\) en el punto \(P\). Demostrar que \(BP\) es perpendicular a \(AD\).
SoluciónSolución. Vamos a probar que \(AB^2+DP^2=AP^2+BD^2\), lo que implica que las dos diagonales del cuadrilátero \(ABDP\) (sombreado en azul en la figura) son perpendiculares (¿sabes probarlo?) y se tiene el resultado deseado. Sea \(X\) el pie de la perpendicular por \(P\) al lado \(AC\). Usando que \(PX=PE\) y \(BD=BE\), así como el teorema de Pitágoras en los triángulos rectángulos \(AXP\) y \(DPE\), tenemos que \[AB^2+DP^2=AB^2+DE^2+PE^2=AB^2+BD^2+PX^2=BD^2+AP^2+AB^2-AX^2,\] luego será suficiente con probar que \(AB=AX\).
Para ello, sean \(F\) y \(G\) los puntos en que la circunferencia inscrita es tangente a los lados \(AB\) y \(AC\), respectivamente. Usando que \(CX=CE\), \(BF=BD=DE\), \(AF=AG\) y \(CG=CD\), tenemos que \[AX=AC-CX=AG+CG-CE=AF+CG-CD-BD+2BD=AF+BF=AB.\]
Este fue el problema 5 de la fase local de la Olimpiada Matemática Española de 2020.
Problema 28 (nivel 2) (propuesto el 19-2-2024) Determinar todos los valores reales de \((x,y,z)\) para los cuales \[\left\{\begin{array}{l}x+y+z=1\\x^2y+y^2z+z^2x=xy^2+yz^2+zx^2,\\x^3+y^2+z=y^3+z^2+x.\end{array}\right.\]
SoluciónSolución. La idea clave es darse cuenta de que la segunda ecuación se puede escribir equivalentemente como \((x-y)(y-z)(x-z)=0\), lo que nos dice que dos de las incógnitas tienen que ser iguales. Como no hay simetría, tendremos que distinguir tres casos:
- Si \(x=y\), entonces la primera ecuación nos dice que \(2x+z=1\). Sustituyendo \(y=x\) y \(z=1-2x\) en la tercera y simplificando, llegamos a la ecuación \(3x^2-x=0\), que nos da soluciones \(x=0\) y \(x=\frac{1}{3}\). Deshaciendo las sustituciones, obtenemos la soluciones al sistema original \((x,y,z)=(0,0,1)\) y \((x,y,z)=(\frac{1}{3},\frac{1}{3},\frac{1}{3})\).
- Si \(y=z\), la primera ecuación nos da \(x+2y=1\), luego podemos sustituir \(z=y\) y \(x=1-2y\) en la tercera ecuación y después de simplificar nos queda \(y(3y^2-4y+1)=0\), que tiene soluciones \(y=0\), \(y=1\) e \(y=\frac{1}{3}\). En el sistema original, esto se corresponde con las soluciones \((1,0,0)\), \((-1,1,1)\) y \((\frac{1}{3},\frac{1}{3},\frac{1}{3})\), aunque esta última ya la hemos obtenido previamente.
- Si \(z=x\), procedemos de forma análoga usando la primera ecuación para obtener \(y=1-2x\). Sustituyendo en la tercera y simplificando, llegamos a que \(x(9x^2-9x+2)=0\), ecuación que tiene por soluciones \(x=0\), \(x=\frac{1}{3}\) y \(x=\frac{2}{3}\). Estas nos dan las soluciones del sistema \((0,1,0)\), \((\frac{1}{3},\frac{1}{3},\frac{1}{3})\) y \((\frac{2}{3},\frac{-1}{3},\frac{2}{3})\).
Se han obtenido así un total de \(7\) soluciones distintas.
Este fue el problema 3 de la fase local de la Olimpiada Matemática Española de 2020.
Problema 27 (nivel 2) (propuesto el 19-2-2024) Dada la sucesión \(a_n=1+n^3\), ¿cuál es el mayor valor que puede tomar \(\text{mcd}(a_n,a_{n+1})\)?
SoluciónSolución. Comenzamos factorizando \begin{align*}a_n&=n^3+1=(n+1)(n^2-n+1),\\a_{n+1}&=(n+1)^3+1=(n+2)(n^2+n+1).\end{align*} Como \(n+1\) no tiene factores en común con \(n+2\) ya que son dos números consecutivos y tampoco con \(n^2+n+1=n(n+1)+1\) ya que es un múltiplo de \(n+1\) más una unidad. De la misma forma, \(n+2\) no tiene factores en común con \(n+1\) pero al ser \(n^2-n+1=(n+2)(n-3)+7\), el único factor no trivial que pueden tener en común \(n+2\) y \(n^2-n+1\) es el \(7\) (justo ocurre cuando \(n+2\) es múltiplo de \(7\)). Finalmente, tenemos que \begin{align*} \mathrm{mcd}(n^2-n+1,n^2+n+1)&=\mathrm{mcd}(n^2-n+1,n^2+n+1-(n^2-n+1))\\&=\mathrm{mcd}(n^2-n+1,2n)=\mathrm{mcd}(n^2-n+1,2)=1,\end{align*} puesto que \(n^2-n+1\) es impar y no tiene factores en común con \(n\). Con todo esto, deducimos que el máximo posible divisor común a \(a_n\) y \(a_{n+1}\) es \(7\). Para \(n=5\), tenemos que \(a_5=126=18\cdot 7\) y \(a_6=217=31\cdot 7\) tienen máximo común divisor \(7\), luego este es el valor buscado.
Este fue el problema 9 de la fase local de la Olimpiada Matemática Española de 2007.
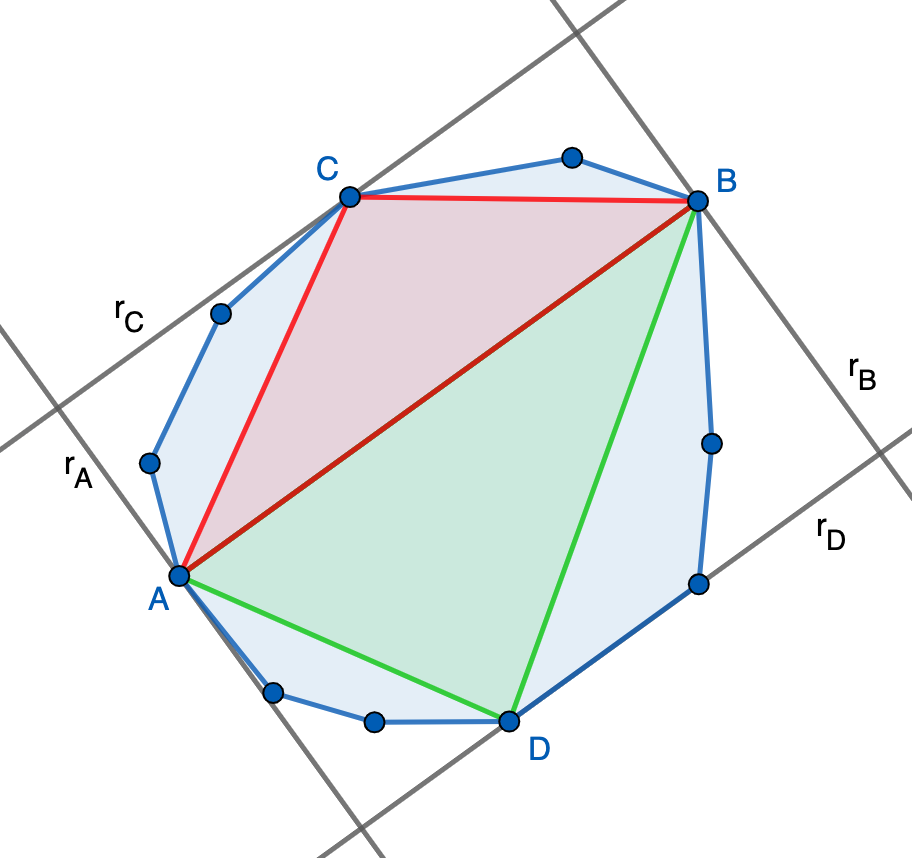
Problema 26 (nivel 3) (propuesto el 12-2-2024) Demostrar que, para cualquier polígono convexo de área \(1\), existe un paralelogramo de área \(2\) que lo contiene.
SoluciónSolución. Sean \(A\) y \(B\) los dos vértices más alejados entre sí del polígono y consideramos los dos vértices \(C\) y \(D\) más alejados de la recta \(AB\) en sendos semiespacios definidos por \(AB\). Trazamos por \(A\) y \(B\) perpendiculares \(r_A\) y \(r_B\) a \(AB\) y por \(C\) y \(D\) paralelas \(r_C\) y \(r_D\) a \(AB\). Estas cuatro rectas \(r_A,r_B,r_C,r_D\) determinan un rectángulo \(R\). Vamos a ver que \(R\) (que es, en particular, paralelogramo) contiene al polígono y que tiene área menor o igual que \(2\).
- En primer lugar, tenemos que ningún vértice se puede salir de la banda determinada por \(r_A\) y \(r_B\) ya que en tal caso dicho vértice tendría distancia con \(A\) o con \(B\) mayor que \(AB\) (¿por qué?), contradiciendo que \(AB\) es el segmento entre vértices de longitud máxima. Por otro lado, ningún vértice se puede salir de la banda determinada por \(r_C\) y \(r_D\) ya que en tal caso dicho vértice distaría de \(AB\) más que \(C\) o \(D\), contradiciendo que estos son los puntos más alejados. Por tanto, todos los vértices del polígono están en \(R\) y, por convexidad, todo el polígono debe estar en \(R\).
- Finalmente, veamos que \(\text{área}(R)\leq 2\). Para ello, observamos que los triángulos \(ACB\) y \(ADB\) están contenidos en el polígono (de nuevo, por convexidad), de donde \[1=\text{área}(\text{polígono})\geq\text{área}(ACB)+\text{área}(ADB)=\tfrac{1}{2}\text{área}(R).\]
Esto termina la demostración. Es importante observar que uno de los dos puntos \(C\) o \(D\) podría no estar definido porque no haya vértices a un lado de la recta \(AB\). En tal caso, se razona de forma similar usando que \(r_C=AB\) o \(r_D=AB\).
Este fue el problema 2 de la Olimpiada Iberoamericana de Matemáticas de 1993.
Problema 25 (nivel 2) (propuesto el 12-2-2024) ¿Existe algún triángulo tal que las medidas de sus lados son tres números enteros consecutivos y el ángulo mayor es el doble que el menor? Si existe, determinar sus medidas.
SoluciónSolución. Pongamos que los lados miden \(n-1,n,n+1\) y que el ángulo menor es \(\alpha\) y el mayor \(2\alpha\). Esto nos dice que \(2\alpha\) es el ángulo opuesto a \(n+1\) y \(\alpha\) el opuesto a \(n-1\) ya que los ángulos guardan el mismo orden que sus lados opuestos. Por tanto, el teorema del seno nos dice que \[\frac{\mathrm{sen}(\alpha)}{n-1}=\frac{\mathrm{sen}(2\alpha)}{n+1}=\frac{2\mathrm{sen}(\alpha)\cos(\alpha)}{n+1}\ \Longrightarrow\ \cos(\alpha)=\frac{n+1}{2(n-1)}.\] Ahora bien, el teorema del coseno aplicado al lado de longitud \(n-1\) nos dice que \[(n-1)^2=n^2+(n+1)^2-2n(n+1)\cos(\alpha)=2n^2+2n+1-\frac{n(n+1)^2}{n-1}.\] Operando y simplificando, la ecuación anterior equivale a \(n(n-5)=0\), lo que nos da como única posibilidad \(n=5\) (el triángulo de lados \(4,5,6\).
Resta por ver si este triángulo cumple la propiedad. De nuevo por el teorema del coseno, tenemos que el ángulo \(\alpha\) opuesto al lado de longitud \(4\) cumple \[\cos(\alpha)=\frac{5^2+6^2-4^2}{2\cdot 5\cdot 6}=\frac{3}{4}.\] Por su parte, el ángulo \(\beta\) opuesto al lado de longitud \(6\) cumple \[\cos(\beta)=\frac{4^2+5^2-6^2}{2\cdot 4\cdot 5}=\frac{1}{8}=2\cos^2(\alpha)-1=\cos(2\alpha).\] Deducimos que \(\beta=2\alpha\), luego en este triángulo el ángulo mayor es el doble del menor y respondemos así afirmativamente a la pregunta del enunciado.
Este fue el problema número 11 de la fase local de la Olimpiada Matemática Española de 2011.
Problema 24 (nivel 3) (propuesto el 5-2-2024) Consideremos la sucesión de enteros positivos \(\{x_n\}\) definida por \(x_1=2\) y \(x_{n+1}=2x_n^3+x_n\) para todo \(n\geq 1\). Hallar la mayor potencia de \(5\) que divide a \(x_{2024}^2+1\).
SoluciónSolución. Se pueden calcular algunos términos, pero rápidamente el resultado se dispara ya que la sucesión crece exponencialmente:\[x_1^2+1=5,\quad x_2^2+1=325,\quad x_3^2+1=136469125,\ldots\] Vamos a probar por inducción sobre \(n\) que \(x_n^2+1\) es múltiplo de \(5^n\) pero no de \(5^{n+1}\). Si probamos esto, tendremos que la solución al problema es \(5^{2024}\). Está claro que el caso \(n=1\) es cierto ya que \(x_1^2+1=5\) es múltiplo de \(5\) pero no de \(25\). También es cierto si \(n=2\) ya que \(x_2^2+1=325\) es múltiplo de \(25\) pero no de \(125\). Supongamos que la propiedad es cierta para \(n\geq 2\), lo que nos permite escribir \(x_n^2+1=5^ny_n\), siendo \(y_n\) no múltiplo de \(5\). Entonces, para \(x_{n+1}\) podemos desarrollar y simplificar \begin{align*}x_{n+1}^2+1&=(2x_n^3+x_n)^2+1=(4x_n^4+4x_n^2+1)x_n^2+1\\&=(4(5^ny_n-1)^2+4(5^ny_n-1)+1)(5^ny_n-1)+1\\&=4\cdot 5^{3n}y_n^3-8\cdot 5^{2n}y_n^2+5^{n+1}y_n\\&=5^{n+1}(4\cdot 5^{2n-1}y_n^3-8\cdot 5^{n-1}y_n^2+y_n).\end{align*}Este número es múltiplo de \(5^{n+1}\) pero no de \(5^{n+2}\) ya que el factor \(4\cdot 5^{2n-1}y_n^3-8\cdot 5^{n-1}y_n^2+y_n\) es congruente con \(y_n\) módulo \(5\). Aquí estamos usando que \(n\geq 2\) para asegurar que \(5^{n-1}\) es múltiplo de \(5\), es decir, en la inducción hemos tenido que comprobar dos casos iniciales.
Este fue (solo cambiando el valor de \(n\)) el problema 4 de la fase nacional de la Olimpiada Matemática Española de 2014.
Problema 23 (nivel 1) (propuesto el 5-2-2024) La última cifra de \(2009^{2011}\) es un nueve pero, ¿cuántos ceros preceden a ese nueve?
SoluciónSolución. Vamos a desarrollar la potencia usando el binomio de Newton. Trabajaremos módulo \(1000\) porque solo nos van a interesar las tres últimas cifras:$$2009^{2011}\equiv 9^{2011}\equiv(10-1)^{2011}\equiv-1+\binom{2011}{1}\cdot 2010-\binom{2011}{2}\cdot 10^2.$$No tenemos que poner más términos porque a partir del siguiente nos quedan múltiplos de \(1000\) (si necesitáramos más cifras sólo habría que trabajar módulo una potencia de \(10\) más grande y añadir más términos al desarrollo). Podemos seguir calculando módulo \(1000\):$$2009^{2011}\equiv -1+11\cdot 10+55\cdot 10^2\equiv-391\equiv 609.$$Por lo tanto, las tres últimas cifras son \(609\) y deducimos que solo hay un cero que precede al nueve.
Este fue el problema 3 de la fase local de la Olimpiada Matemática Española de 2011.
Problema 22 (nivel 2) (propuesto el 29-1-2024) Probar que el producto de cuatro naturales consecutivos no puede ser un cuadrado perfecto.
SoluciónSolución. Pongamos que los números son \(n-1,n,n+1,n+2\) por simplicidad, luego su producto \(P\) puede expresarse después de completar el cuadrado como \begin{align*}P=(n-1)n(n+1)(n+2)&=(n^3-n)(n+2)\\&=n^4+2n^3-n^2-2n=(n^2+n-1)^2-1.\end{align*}Por tanto, \(P\) es una unidad menos que un cuadrado perfecto; si \(P\) fuera a su vez un cuadrado perfecto, entonces la única posibilidad es \(P=0\), contradiciendo que \(P\) es el producto de cuatro naturales (positivos).
Este problema es parte del problema 5 de la fase nacional de la Olimpiada Matemática Española de 2006 (en ese problema se pedía también demostrar que no puede ser un cubo perfecto, ¿te atreves a resolverlo?).
Problema 21 (nivel 1) (propuesto el 29-1-2024) Sea \(P(x)\) un polinomio con coeficientes enteros. Demostrar que si existe un entero \(k\geq 2\) tal que ninguno de los enteros \(P(1),P(2),\ldots,P(k)\) es divisible por \(k\), entonces \(P(x)\) no tiene raíces enteras.
SoluciónSolución. Vamos a probar el contrarrecíproco, es decir, si \(P(x)\) tiene alguna raíz entera \(\alpha\), entonces alguno de los enteros \(P(1),P(2),\ldots,P(k)\) es divisible por \(k\). Que \(\alpha\in\mathbb{Z}\) sea raíz quiere decir que \(P(x)=(x-\alpha)Q(x)\). Ahora bien, debe existir un entero \(j\) tal que \(1\leq j\leq k\) y \(j\equiv \alpha\ (\text{mod }k)\). Evaluando en este entero, tenemos que \(P(j)=(j-\alpha)Q(j)\) es múltiplo de \(k\) ya que \(j-\alpha\) lo es.
Este fue el problema 1 en la fase nacional de la Olimpiada Matemática Española de 2006.
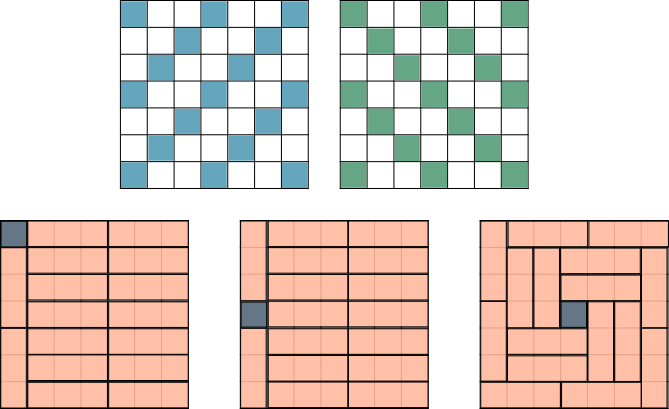
Problema 20 (nivel 3) (propuesto el 22-1-2024) Un tablero \(7\times 7\) está recubierto por \(16\) fichas rectangulares de tamaño \(3\times 1\) y una más de tamaño \(1\times 1\). ¿En qué posiciones debe estar la ficha \(1\times 1\) para que esto sea posible?
SoluciónSolución. Pintamos algunas casillas del tablero de color verde y otras de color azul siguiendo las diagonales como indica la imagen. Hemos hecho dos dibujos ya que algunas casillas serán tanto verdes como azules. Como hay 17 casillas verdes y 17 azules y cada ficha \(3\times 1\) ocupa solo una verde y solo una azul, necesariamente la ficha \(1\times 1\) debe estar en una casilla que sea tanto verde como azul, es decir, en un vértice, en la casilla media de un lado o en el centro. Vemos en la imagen (parte de abajo) que en todos estos casos es posible hacer el recubrimiento, luego son las únicas posibilidades para la ficha \(1\times 1\).
Problema 19 (nivel 2) (propuesto el 22-1-2024) Dado un entero \(n\gt 1\), demostrar que \(n^{n-1}-1\) es divisible por \((n-1)^2\).
SoluciónSolución. En primer lugar, usando la suma de los términos de una progresión geométrica, tenemos que $$S=\frac{n^{n-1}-1}{n-1}=n^{n-2}+n^{n-3}+n^{n-4}+\ldots+n+1$$
es un número entero. Veamos que podemos dividir \(S\) de nuevo por \(n-1\) y seguir obteniendo un entero. Para ello, sumamos y restamos convenientemente potencias de \(n\) y expresamos \(S\) como \begin{align*}S&=[n^{n-2}-n^{n-3}]+[2n^{n-3}-2n^{n-4}]\\&\qquad+[3n^{n-4}-3n^{n-5}]+\ldots+[(n-2)n^1-(n-2)n^0]+[n-1].\end{align*}
Ahora bien, está claro que cada uno de los corchetes es múltiplo de \(n-1\), luego también lo es \(S\).
Problema 18 (nivel 1) (propuesto el 15-1-2024) Sea \(ABCD\) un cuadrilátero con \(\angle ABC = \angle ADC = 90^\circ\), \(\angle BAD = 60^\circ\), \(AB = 7\) y \(AD = 8\). Calcular la longitud de \(BC\) y \(CD\).
SoluciónSolución. Llamemos \(x=BC\) e \(y=CD\) por simplicidad. El teorema del coseno aplicado a los triángulos \(ABD\) y \(CBD\) nos dice que $$BD^2=7^2+8^2-2\cdot 7\cdot 8\cos(60)=57,$$ $$57=BD^2=x^2+y^2-2x\cos(120)=x^2+y^2+xy.$$Por otro lado, el teorema de Pitágoras aplicado a los triángulos \(ABC\) y \(CDA\) nos dice que $$7^2+x^2=AC^2=8^2+y^2\ \Rightarrow\ x^2-y^2=64-49=17.$$ Tenemos así un sistema de dos ecuaciones cuadráticas con incógnitas \(x\) e \(y\). Es fácil resolverlo (se deja como ejercicio) para llegar a que la única solución positiva es \((x,y)=(3\sqrt{3},2\sqrt{3})\).
Este fue el problema 3 de segundo nivel de la fase regional de la Olimpiada Matemática Argentina.
Problema 17 (nivel 1) (propuesto el 15-1-2024) ¿Qué dígitos se han omitido en la siguiente multiplicación?$$\begin{matrix} &2&*&*\\\times&&*&*\\\hline &*&6&1\\ *&*&*&\\\hline *&*&0&1\end{matrix}$$
SoluciónSolución. Probando a resolver dígito por dígito desde las unidades a las centenas, se llega fácilmente a la siguiente solución única:$$\begin{matrix} &2&8&7\\\times&&2&3\\\hline &8&6&1\\ 5&7&4&\\\hline 6&6&0&1\end{matrix}$$Este fue el problema 1 en la fase local de la Olimpiada Matemática Española de 1999.
Problema 16 (nivel 2) (propuesto el 8-1-2024) Determinar todas las ternas de números reales \((x,y,z)\) que cumplen el siguiente sistema de ecuaciones:$$\left.\begin{array}{r}xyz=8\phantom{3}\\x^2y+y^2z+z^2x=73\\x(y-z)^2+y(z-x)^2+z(x-y)^2=98\end{array}\right\}$$
SoluciónSolución. Desarrollando los cuadrados en la tercera ecuación y usando las dos primeras se llega fácilmente a que$$xy^2+yz^2+zx^2=73.$$ Restando la segunda ecuación del enunciado y esta que hemos obtenido, llegamos a que $$0=73-73=xy^2+yz^2+zx^2-x^2y-y^2z-z^2x=(y-x)(z-y)(x-z).$$ Por lo tanto, dos de las incógnitas deben ser iguales, pongamos que \(y=z\) sin perder generalidad. Entonces, las tres ecuaciones del enunciado se transforman en las dos siguientes:$$\left.\begin{array}{r}xy^2=8\phantom{3}\\x^2y+y^3+xy^2=73\end{array}\right\}$$ (la tercera ecuación ya no nos hace falta porque es redundante). Esto nos dice que \(x^2y+y^3=65\) y, multiplicando por \(y^3\), tenemos que \(64+y^6=(xy^2)^2+y^6=65y^3\). En consecuencia, \(y\) debe ser solución de la ecuación bicúbica \(y^6-65y+64=0\), que puede factorizarse como \((y^3-1)(y^3-64)=0\), lo que nos da las soluciones \(y=1\) e \(y=4\). Como \(xy^2=8\) y \(z=y\), tenemos que \((x,y,z)=(8,1,1)\) o bien \((x,y,z)=(\tfrac{1}{2},4,4)\). Ahora bien, cualquier permutación de las variables también da una solución (hemos roto la simetría al suponer que \(y=z\), luego tenemos seis soluciones para \((x,y,z)\):$$(8,1,1),\quad (1,8,1),\quad (1,1,8),\quad (\tfrac{1}{2},4,4),\quad (4,\tfrac{1}{2},4),\quad (4,4,\tfrac{1}{2}).$$
Este fue el problema número 1 de la Olimpiada Iberoamericana de Matemáticas de 2005.
Problema 15 (nivel 1) (propuesto el 8-1-2024) Observa las siguientes sumas:\begin{eqnarray*}1^3+5^3+3^3&=&153,\\16^3+50^3+33^3&=&165033,\\166^3+500^3+333^3&=&166500333,\\1666^3+5000^3+3333^3&=&166650003333,\ldots\end{eqnarray*} Demuestra que estas sumas son correctas incluso si seguimos añadiendo dígitos a los sumandos.
SoluciónSolución. Observamos que, para \(n\) dígitos, tenemos que $$166\ldots6=\tfrac{10^n-4}{6},\quad 500\ldots0=5\cdot 10^{n-1},\quad 133\ldots3=\tfrac{10^n-1}{3}.$$ Por tanto, la igualdad que queremos demostrar se expresa como $$\left(\tfrac{10^n-4}{6}\right)^3+(5\cdot 10^{n-1})^3+\left(\tfrac{10^n-1}{3}\right)^3=\tfrac{10^n-4}{6}\cdot 10^{2n}+(5\cdot 10^{n-1})\cdot 10^n+\left(\tfrac{10^n-1}{3}\right).$$ Ahora sólo hay que desarrollar los cubos y agrupar las potencias de \(10^n\) resultantes para ver que la igualdad anterior es cierta para todo número natural \(n\) (se deja como ejercicio).
Problema 14 (nivel 1) (propuesto el 1-1-2024) Halla tres números primos \(p,q,r\) sabiendo que \(r-q=2p\) y \(rq+p^2=676\).
SoluciónSolución. Sustituyendo \(r=2p+q\) en la segunda ecuación nos queda \(676=(2p+q)q+p^2=(p+q)^2\), luego tiene que ser \(p+q=26\). Las formas de expresar \(26\) como suma de dos primos son $$26=3+23=7+17=13+13=17+7=23+3$$ y de todas ellas la única que cumple que \(r=2p+q\) es primo es \(p=3\) y \(q=23\), que nos da \(r=29\).
Este es (con una pequeña modificación) el problema 1 de la fase local de la Olimpiada Matemática Española de 2001.
Problema 13 (nivel 2) (propuesto el 1-1-2024) El n-ésimo número triangular se define como \(T_n=1+2+\ldots+n\). Hallar todos los valores de \(n\) para los que el producto de los 16 números triangulares consecutivos \(T_nT_{n+1}\cdots T_{n+15}\) es un cuadrado perfecto.
SoluciónSolución. Es bien conocido que \(T_n=\frac{n(n+1)}{2}\), luego podemos escribir \begin{eqnarray*}T_nT_{n+1}\cdots T_{n+15}&=&\frac{n(n+1)^2(n+2)^2\cdots(n+15)^2(n+16)}{2^{16}}\\&=&n(n+16)\cdot \left(\frac{(n+1)(n+2)\cdots(n+15)}{2^{8}}\right)^2\end{eqnarray*}La fracción anterior con denominador \(2^8\) es un número entero ya que en su numerador habrá al menos siete factores pares y más de uno múltiplo de \(4\). Por tanto, el problema se reduce a encontrar los naturales \(n\) tales que \(n(n+16)=a^2\) para cierto entero \(a\). Completando el cuadrado, podemos escribir esta ecuación como \((n+8)^2-a^2=64\) o bien \((n+8-a)(n+8+a)=64\). Esto nos dice que \(n+8-a\) y \(n+8+a\) son potencias de \(2\) cuyo producto es \(64\). Además, como \(n+8-a\lt n+8+a\), las únicas posibilidades son \begin{eqnarray*}n+8-a=1,\quad n+8+a=64,\\n+8-a=2,\quad n+8+a=32,\\n+8-a=4,\quad n+8+a=16.\end{eqnarray*} Resolviendo los sistemas lineales que se obtienen, llegamos a que 1 y 64 no dan ninguna solución entera, 2 y 32 dan \(n=9\) y 4 y 16 dan \(n=2\). Deducimos que \(n=2\) y \(n=9\) son las únicas soluciones.
Este es el problema 12 de la fase local de la Olimpiada Matemática Española de 2016.
Problema 12 (nivel 2) (propuesto el 25-12-2023) ¿Cuántas soluciones enteras tiene la ecuación \(a+b+c+d=2024\) de forma que \(a,b,c,d\geq 0\)?
SoluciónSolución. El problema equivale a poner \(2027\) bolas en fila y elegir tres de ellas como separadores: el número \(a\) será el número de bolas hasta la primera elegida, \(b\) será el número de bolas entre la primera y la segunda, \(c\) el número de bolas entre la segunda y la tercera y \(d\) el número de bolas de la tercera hasta el final. Por tanto, la solución es el número de formas diferentes de elegir tres elementos de un conjunto de 2027, es decir $$\binom{2027}{3}=\frac{2027\cdot 2026\cdot 2025}{3\cdot 2\cdot 1}=1386011925.$$
Problema 11 (nivel 2) (propuesto el 25-12-2023) Dos jugadores juegan al tres en raya en tres dimensiones (en un tablero \(3\times 3\times 3\)) poniendo alternativamente sus fichas y gana, como es usual, el que consiga tener tres fichas alineadas y empatan si no gana ninguno de ellos. Demuestra que en esta versión del juego no puede haber empate.
SoluciónSolución. Vamos a suponer que hay un empate para llegar a una contradicción. Supongamos que el jugador A ha ocupado el centro (A no tiene por qué ser el primer jugador), luego al menos uno de los centros de cada par de caras opuestas tienen que estar ocupados por el otro jugador B. Esto nos asegura que hay tres caras \(C_1,C_2,C_3\) con un vértice común \(V\) y cuyos centros están ocupados por B. En primer lugar, supongamos que el vértice \(V\) está ocupado por B. En tal caso, los vértices opuestos a \(V\) en \(C_1,C_2,C_3\) deben ser de A y, como el centro también es de A, los otros vértices de \(C_1,C_2,C_3\) deben ser de B. Esto nos dice que hay diagonales de \(C_1,C_2,C_3\) cuyas tres casillas las ha ocupado B (contradicción). En segundo lugar, supongamos que \(V\) está ocupado por A. Si la casilla central \(C_{12}\) de la arista común a \(C_1\) y \(C_2\) está ocupada por B, completando casillas para que no haya tres alineados, se llega fácilmente a contradicción. Por tanto las casillas \(C_{12}\), \(C_{23}\) y \(C_{13}\) tienen que estar ocupadas por A con un razonamiento similar. Completando de nuevo casillas para que no haya tres del mismo jugador alineadas, se llega a contradicción de nuevo.
Problema 10 (nivel 1) (propuesto el 18-12-2023) Consideremos la función lineal \(f(x)=ax+b\). Supongamos que al aplicar repetidamente esta función 2023 veces, obtenemos \[f(f(f(\ldots f(x)\ldots)))=x,\quad \text{para todo }x\in\mathbb{R}.\] Hallar los valores de \(a\) y \(b\).
SoluciónSolución. Observemos que $$f(f(x))=f(ax+b)=a(ax+b)+b=a^2x+ab+b,$$ $$f(f(f(x)))=a^2(ax+b)+ab+b=a^3x+a^2b+ab+b,$$
$$f(f(f(f(x))))=a^3(ax+b)+a^2b+ab+b=a^4x+a^3b+a^2b+ab+b.$$
De esta forma, es claro que aplicar la función 2023 veces resulta en la función lineal $$a^{2022}x+(a^{2023}+a^{2022}+\ldots+a+1)b.$$ Para que la función sea igual a la identidad para todo valor de \(x\), tiene que ser el coeficiente de \(x\) igual a \(1\) y el término independiente \(0\). Por un lado, \(a^{2022}=1\) nos lleva a que \(a=\pm 1\). Si \(a=1\), entonces el término independiente es \(2024b\), luego tiene que ser \(b=0\); si \(a=-1\), entonces el término independiente es automáticamente cero. Esto nos dice que las funciones que buscamos son \(f(x)=x\) y \(f(x)=-x+b\) para cualquier \(b\in\mathbb{R}\).
Este fue (con un pequeño cambio) el problema 4 de la fase local de la Olimpiada Matemática Española del año 2000.
Problema 9 (nivel 1) (propuesto el 18-12-2023) Supongamos que la sucesión \(a_n\) está definida como \(a_1=3\) y \(a_{n+1}=a_n+a_n^2\) para todo natural \(n\). Hallar las dos últimas cifras de \(a_{2023}\).
SoluciónSolución. Las dos últimas cifras de \(a_n\) sólo dependen de las dos últimas cifras de \(a_{n-1}\), luego bastará calcular algunos términos hasta que se repitan las dos últimas cifras. Haciendo esto, obtenemos la siguiente sucesión de últimas cifras $$03\to 12\to 56\to 92\to 56\to 92\to 56\to 92\to\ldots$$ De esta forma, salvo los dos primeros, los siguientes se repiten por parejas. En particular, las dos últimas cifras de \(a_{2023}\) son las mismas que las de \(a_3\), luego la respuesta a la pregunta es \(56\).
Este fue (con un pequeño cambio) el problema 1 de la fase local de la Olimpiada Matemática Española del año 2000.
Problema 8 (nivel 1) (propuesto el 11-12-2023) Un triángulo tiene lados \(a\), \(b\) y \(c\). Demuestra que hay otro triángulo de lados \(\sqrt{a}\), \(\sqrt{b}\) y \(\sqrt{c}\) y también que no tiene por qué existir un triángulo de lados \(a^2\), \(b^2\) y \(c^2\).
SoluciónSolución. Dadas las longitudes de los lados de un triángulo, para que dicho triángulo exista es suficiente con que la longitud del lado más largo sea menor que la suma de las longitudes de los otros dos. Por ejemplo, tenemos un triángulo de lados \(3\), \(4\) y \(6\) ya que \(3+4\gt 6\), pero no tenemos un triángulo de lados \(3^2=9\), \(4^2=16\) y \(6^2=36\) ya que \(9+16\lt 36\). Esto responde además a la segunda pregunta del enunciado.
Para responder a la primera pregunta, observamos que si \(a\leq b\leq c\), entonces \(\sqrt{a}\leq \sqrt{b}\leq \sqrt{c}\). Lo que tenemos que demostrar es que si \(c\lt a+b\), entonces \(\sqrt{c}\lt\sqrt{a}+\sqrt{b}\). Esto último equivale a que \(c\lt (\sqrt{a}+\sqrt{b})^2=a+b+2\sqrt{ab}\), lo cual es claramente cierto ya que hemos supuesto que \(c\lt a+b\).
Problema 7 (nivel 2) (propuesto el 11-12-2023) Supongamos que \(a,b,c\) son números reales positivos. ¿Es posible que los tres números \(a-ab\), \(b-bc\) y \(c-ac\) sean todos ellos mayores que \(\frac{1}{4}\)?
SoluciónSolución. Supongamos que \(a-ab\), \(b-bc\) y \(c-ac\) son mayores que \(\frac{1}{4}\). Esto implica claramente que \(a\lt 1\), \(b\lt 1\) y \(c\lt 1\) ya que estamos suponiendo que \(a\), \(b\) y \(c\) son positivos. Multiplicando y reordenando términos, obtenemos que\[a(1-a)b(1-b)c(1-c)=(a-ab)(b-bc)(c-ac)\gt\frac{1}{64}.\]Sin embargo, tenemos que \(0\leq x(1-x)=x-x^2=\frac{1}{4}-(\frac{1}{2}-x)^2\leq\frac{1}{4}\) siempre que \(0\leq x\leq 1\). Por tanto,\[a(1-a)b(1-b)c(1-c)\leq\frac{1}{4}\cdot\frac{1}{4}\cdot\frac{1}{4}=\frac{1}{64}.\]Hemos obtenido así una contradicción, que nos dice que los tres números del enunciado no pueden ser a la vez mayores que \(\frac{1}{4}\).
Problema 6 (nivel 1) (propuesto el 4-12-2023) En cada casilla de las tres filas inferiores de un tablero de ajedrez \(8\times 8\) se coloca una ficha. Si cada ficha puede saltar por encima de otra en horizontal, vertical o diagonal, ¿es posible realizar este tipo de movimientos repetidamente para colocar las 24 fichas iniciales en las tres filas superiores?
SoluciónSolución. Si numeramos la filas consecutivamente del 1 al 8, siendo 1 la fila inferior y 8 la superior, entonces tenemos originalmente 16 fichas en fila impar y 8 en fila par. Esto no cambia cuando una ficha salta por encima de otra ya que cae en una fila con la misma paridad. Por lo tanto, no se puede llegar a rellenar las tres filas superiores ya que en tal caso habría 8 fichas en fila impar y 16 en fila par.
Este problema (con otro enunciado) apareció en la fase local de la Olimpiada Matemática Española (2004, problema 2).
Problema 5 (nivel 2) (propuesto el 4-12-2023) Los números del 1 al 9 se escriben en las casillas de una tabla \(3\times 3\). Se toman los tres números de tres cifras que se leen en las filas de izquierda a derecha y los tres que se leen en columnas de arriba abajo y sea \(S\) la suma de estos seis números. ¿Se pueden colocar los números para que \(S=2024\)? ¿Y \(S=2027\)?
SoluciónSolución. Llamemos \(A,B,C,D,E,F,G,H,I\) a los nueve números ordenados de izquierda a derecha y de arriba abajo. Como un número es congruente con la suma de sus cifras módulo 9, se tiene que \begin{align*}
S\equiv&(A+B+C)+(D+E+F)+(G+H+I)\\&+(A+D+G)+(B+E+H)+(C+F+I)\ (\text{mod } 9)\end{align*}Como la suma de los nueve números es igual a 45, se tiene que \(S\equiv 90\equiv 0\ (\text{mod }9)\). Como \(2024\equiv 8\ (\text{mod }9)\), claramente no puede obtenerse \(S=2024\). El mismo razonamiento no sirve para \(2025\equiv 0\ (\text{mod }9)\), pero es que en tal caso sí se puede. Para demostrarlo, es suficiente ver una disposición en que obtenga esta suma, por ejemplo escribiendo (por filas) 143, 297 y 586.
Este problema (con otro enunciado) apareció en la fase nacional de la Olimpiada Matemática Española (2001, problema 4).
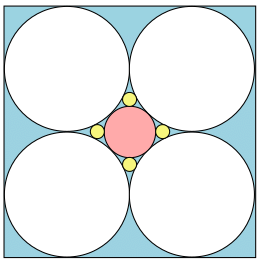
Problema 4 (nivel 1) (propuesto el 27-11-2023) El cuadrado de la figura tiene lado igual a 2 y en él hemos inscrito algunas circunferencias tangentes entre sí. Calcula los radios de las circunferencias amarillas.
 Solución
SoluciónSolución. Está claro que cada circunferencia blanca tiene radio \(\frac{1}{2}\). Además, llamamos \(r\) al radio de la circunferencia roja y \(s\) al radio de las circunferencias amarillas. Si dos circunferencias son tangentes, entonces el punto de tangencia está alineado con los centros, luego en la figura del enunciado encontramos la configuración que se indica en la figura de abajo. En primer lugar, tenemos un triángulo rectángulo isósceles de catetos iguales a \(\frac{1}{2}\) e hipotenusa \(\frac{1}{2}+r\), luego el teorema de Pitágoras nos dice que \[(\tfrac{1}{2}+r)^2=(\tfrac{1}{2})^2+(\tfrac{1}{2})^2=\tfrac{1}{2}\ \Leftrightarrow\ r=\tfrac{\sqrt{2}}{2}-\tfrac{1}{2}=\tfrac{\sqrt{2}-1}{2}.\] Por otro lado, también tenemos un triángulo rectángulo de catetos \(\frac{1}{2}\) y \(\frac{1}{2}-r-s\) e hipotenusa \(\frac{1}{2}+s\), luego el teorema de Pitágoras de nuevo nos dice que \[(\tfrac{1}{2}+s)^2=(\tfrac{1}{2})^2+(\tfrac{1}{2}-r-s)^2\ \Leftrightarrow\ s=\frac{1-4r+4r^2}{8(r-1)}=\frac{5-3\sqrt{2}}{14}.\]

Problema 3 (nivel 2) (propuesto el 27-11-2023) Tenemos un cuadrilátero con la propiedad de que, al trazar cualquiera de sus dos diagonales, esta lo divide en dos triángulos de igual área. Demostrar que el cuadrilátero es un paralelogramo.
SoluciónSolución. Llamemos \(ABCD\) al cuadrilátero (que tiene que ser convexo ya que en caso contrario una de las diagonales no lo dividiría en dos triángulos). Al trazar la diagonal \(AC\), como los triángulos \(ABC\) y \(ACD\) tienen la misma área y el lado común \(AC\), también ha de ser igual la altura sobre este lado, es decir, \(B\) y \(D\) están a la misma distancia de \(AC\) (uno a cada lado de esta recta por ser el cuadrilátero convexo), luego el punto medio de \(BD\) está sobre \(AC\) (\(\star\)). De la misma forma se prueba que el punto medio de \(AC\) está sobre \(BD\), luego las diagonales se cortan en su punto medio y el cuadrilátero debe ser un paralelogramo (\(\star\)).
¿Sabrías justificar las dos afirmaciones marcadas con la estrella (\(\star\))? Este problema apareció en la fase local de la Olimpiada Matemática Española de 2008 (problema 2).
Problema 2 (nivel 2) (propuesto el 20-11-2023) Supongamos que tenemos \(n\) enteros positivos que suman \(2n\). ¿Cuáles pueden ser estos números si sabemos además que no se pueden separar en dos subconjuntos que tengan la misma suma?
SoluciónSolución. No es difícil darse cuenta de que si \(n-1\) números son iguales a \(1\) y el \(n\)-ésimo es igual a \(n+1\), entonces suman \(2n\) y no se pueden separar en dos subconjuntos de suma \(n\). Otra posibilidad que surge si analizamos un poco el problema es que todos sean iguales a \(2\) y \(n\) sea impar. Veremos que no hay más posibilidades si probamos que, en cualquier otra circunstancia, los números se pueden dividir en dos subconjuntos de igual suma. Por lo tanto, podremos suponer que hay al menos un número mayor que \(2\) y ningún número mayor o igual que \(n\).
Si partimos de todos los números iguales a \(2\), entonces cualquier otra configuración puede obtenerse quitando unidades a ciertos doses para añadírselas a otros. Esto quiere decir que por cada 3 habrá un 1, por cada 4 habrá dos 1, por cada 5 habrá tres 1 y así sucesivamente. Dicho esto, la estrategia es como sigue: ordenamos los números de mayor a menor como \(a_1\geq a_2\geq\ldots\geq a_n\) y los vamos sumamos empezando del mayor al menor hasta encontrar \(k\) tal que \(a_1+a_2+\ldots+a_k\geq n\). Se tiene que \(k\geq 2\) ya que hemos supuesto que todos son menores que \(n\). Ahora bien, \(a_1\geq 3\) implica la existencia de \(a_1-2\) unos y \(a_2\) implica la existencia de \(a_2-2\). Distingamos dos casos
- Si \(a_1\geq 4\), entonces tenemos al menos \(a_1-2+a_2-2\geq a_2\) unos, luego podemos cambiarlos por \(a_2\) en la suma \(a_1+a_2+\ldots+a_k\geq n\) y eliminar los que sean necesarios para que la suma sea ahora igual a \(n\).
- Si \(a_1=3\), entonces nuestra familia de números está formada solo por treses, doses y unos, con igual número de treses que de unos. Es fácil ver que en tal caso, pueden repartirse en dos subconjuntos con igual suma distinguiendo si hay un número impar o par de doses (se deja como ejercicio).
Este problema apareció en la Olimpíada Matemática Argentina (Certamen Nacional 1999, segundo nivel, problema 6)
Problema 1 (nivel 1) (propuesto el 20-11-2023) En una calculadora sólo funcionan tres teclas: el ocho [8], la suma [+] y el igual [=]. Inicialmente, el número que aparece en la pantalla es 0 y después de pulsar una cierta combinación de teclas, aparece el resultado 1000. ¿Cuántas teclas hemos pulsado? (Da todas las respuestas posibles).
SoluciónSolución. Todas las operaciones permitidas por calculadora se reducen a sumar una cierta cantidad de números formados por ochos (8, 88, 888,...). No podemos usar números con más de tres ochos porque nos pasamos de 1000 (ni tampoco más de un 888). Además, el número de pulsaciones no depende de en qué orden se escriban los números. Esto nos deja con ciertos casos posibles:
- Si usamos un sumando 888, entonces podemos poner \[888+88+8+8+8=1000\]
o bien
\[888+8+8+8+8+8+8+8+8+8+8+8+8+8+8=1000,\]
ya que si ponemos dos o más sumandos 88, entonces nos pasamos de 1000. La primera opción nos da 13 pulsaciones y la segunda 32.
- Si no usamos el 888, entonces todo dependerá de cuántos números pongamos iguales a 88 (tiene que haber entre cero y once ya que \(12\cdot 88=1056\gt1000\). Pongamos que hay \(0\leq n\leq 11\) sumandos 88, lo que nos da un total de \(\frac{1000-88n}{8}=125-11n\) sumandos 8. Cada sumando 88 necesita 3 pulsaciones y cada sumando 8 dos, luego el número de pulsaciones es \(2n+3(125-11n)=475-31n\) para cualquier \(0\leq n\leq 11\).
Este problema apareció (con un enunciado diferente) en la Olimpiada Matemática Argentina (Certamen Regional 2006, nivel 2, problema 2).



 Solución
Solución

