Problemas del curso 2024-25
Problema 32 (nivel 2) (propuesto el 13-2-2025) Determinar un número de cinco cifras tal que su cuadrado termine en las mismas cinco cifras colocadas en el mismo orden.
SoluciónSolución. Si llamamos \(n\) al número en cuestión, la condición del enunciado nos dice que \(n^2-n=n(n-1)\) debe ser múltiplo de \(100000=2^5\cdot 5^5\). Como \(n\) y \(n-1\) son primos entre sí, uno de ellos debe ser múltiplo de \(2^5=32\) y el otro un múltiplo (impar) de \(5^5=3125\). Distingamos las dos posibilidades:
- Si \(n=3125k\), entonces \(n-1=3125k-1\equiv 0\ (\text{mod }32)\), lo cual equivale a que \(21k\equiv 1\ (\text{mod }32)\). El inverso de \(21\) módulo \(32\) es \(29\) (¿sabrías calcularlo?), luego tenemos que \(k\equiv 29\ (\text{mod }32)\), es decir, \(n=3125(32j+29)=100000j+90625\) para cierto entero \(j\). Como \(n\) debe tener cinco cifras, necesariamente \(j=0\) y debe ser \(n=90625\).
- Si \(n-1=3125k\), entonces \(n=3125k+1\equiv 0\ (\text{mod }32)\), luego \(21k\equiv -1\ (\text{mod }32)\) y obtenemos \(k\equiv -29\equiv 3\ (\text{mod }32)\). Esto nos dice que \(n=3125(32j+3)+1=100000j+9376\) para cierto entero \(j\), luego debe ser \(j=0\) y \(n=9376\).
Aunque lo anterior ya nos lo confirma, no está de más comprobar que tanto \(n=90625\) como \(n=09376\) cumplen la condición del enunciado, aunque habría que descartar el segundo si no lo admitimos como número de \(5\) cifras.
Este fue el problema 2 de la fase nacional de la Olimpiada Matemática Española de 1984.
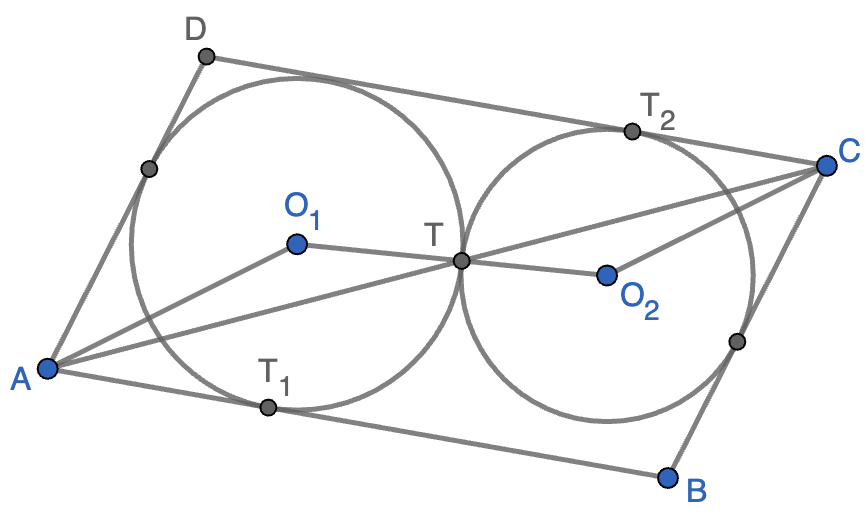
Problema 31 (nivel 1) (propuesto el 13-2-2025) En el interior de un paralelogramo \(ABCD\) se dibujan dos circunferencias. Una es tangente a los lados \(AB\) y \(AD\) y la otra es tangente a los lados \(CD\) y \(CB\). Probar que, si estas circunferencias son tangentes entre sí, el punto de tangencia está en la diagonal \(AC\).
SoluciónSolución. Sean \(O_1\) y \(r_1\) el centro y el radio de la circunferencia tangente a \(AB\) y \(AD\) y sean \(O_2\) y \(r_2\) el centro y el radio de la circunferencia tangente a \(CD\) y \(CB\). Pongamos también que estas circunferencias son tangentes a \(AB\) y \(CD\) en los puntos \(T_1\) y \(T_2\), respectivamente, y que ambas circunferencias son tangentes entre sí en el punto \(T\), que está alineado con \(O_1\) y \(O_2\). Las rectas \(AO_1\) y \(CO_2\) son paralelas puesto que son las bisectrices del paralelogramo en los vértices opuestos. Estas dos paralelas cortan a la recta \(O_1O_2\) formando ángulos alternos internos iguales, es decir, \(\angle AO_1T=\angle CO_2T\). Además, los triángulos \(AO_1T_1\) y \(CO_2T_2\) son triángulos rectángulos semejantes, luego\[\frac{AO_1}{O_1T}=\frac{AO_1}{O_1T_1}=\frac{CO_2}{O_2T_2}=\frac{CO_2}{O_2T}.\]Todo esto nos dice que los triángulos \(AO_1T\) y \(CO_2T\) son semejantes y, en particular, \(\angle CTO_2=\angle ATO_1\). Como \(O_1\), \(O_2\) y \(T\) están alineados, esto implica que \(T\) está alineado con \(A\) y \(C\), como queríamos probar.
Problema 30 (nivel 1) (propuesto el 6-2-2025) Hallar los valores del número real \(a\) para los que todas las raíces del polinomio \(p(x)=x^3-2x^2-25x+a\) son números enteros.
SoluciónSolución. Si llamamos \(\alpha,\beta,\gamma\) a las tres raíces de \(p(x)\), entonces podemos escribir \begin{align*} p(x)&=(x-\alpha)(x-\beta)(x-\gamma)\\&=x^3-(\alpha+\beta+\gamma)x^2+(\alpha\beta+\beta\gamma+\gamma\alpha)x-\alpha\beta\gamma,\end{align*}de modo que identificando coeficientes obtenemos las relaciones de Cardano-Vieta:\[\alpha+\beta+\gamma=2,\qquad \alpha\beta+\beta\gamma+\gamma\alpha=-25,\qquad\alpha\beta\gamma=a.\] Esto nos permite calcular \[\alpha^2+\beta^2+\gamma^2=(\alpha+\beta+\gamma)^2-2(\alpha\beta+\beta\gamma+\gamma\alpha)=4+2\cdot 25=54.\] Las raíces son números enteros y las únicas formas de escribir \(54\) como suma de tres cuadrados son \(49+4+1\), \(36+9+9\) y \(25+25+4\). Reordenando las raíces si es necesario, distinguimos tres casos:
- Si \(\alpha=\pm 7\), \(\beta=\pm 2\) y \(\gamma=\pm 1\), es imposible que se cumpla que \(\alpha+\beta+\gamma=2\) (el sumando \(\alpha=\pm 7\) es demasiado grande en valor absoluto para que sumarle \(\beta+\gamma\) lo hagan igual a \(2\)), luego no hay soluciones en este caso.
- Si \(\alpha=\pm 6\), \(\beta=\pm 3\) y \(\gamma=\pm 3\), también es imposible que se cumpla que \(\alpha+\beta+\gamma=2\) ya que \(\alpha+\beta+\gamma\) siempre dará un múltiplo de tres independientemente de los signos elegidos.
- Si \(\alpha=\pm 5\), \(\beta=\pm 5\) y \(\gamma=\pm 2\), entonces la condición \(\alpha+\beta+\gamma=2\) fuerza a que \(\alpha=5\), \(\beta=-5\) y \(\gamma=2\) (salvo posiblemente intercambiar \(\alpha\) y \(\beta\)). Tenemos entonces que \(\alpha\beta\gamma=5\cdot(-5)\cdot 2=-50\), luego \(a=50\) único valor que cumple la condición del enunciado.
Problema 29 (nivel 1) (propuesto el 6-2-2025) El precio de un diamante es proporcional al cuadrado de su peso. Demostrar que, rompiéndolo en dos partes, existe una depreciación de su valor. ¿Cuándo es máxima dicha depreciación?
SoluciónSolución. Supongamos que rompemos el diamante de peso \(p\) en dos trozos de pesos \(x\) e \(y\), luego el precio original y el precio tras romperlo son proporcionales a \(p^2=(x+y)^2\) y \(x^2+y^2\), respectivamente. La depreciación guardará la misma proporción con \((x+y)^2-x^2-y^2=2xy\), luego nos estamos preguntando cuándo será máximo \(2xy\) sujetos a la restricción \(x+y=p\). De aquí podemos despejar \(2xy=2x(p-x)\), con lo que queremos hallar el máximo de \(f(x)=2x(p-x)\). Esta parábola se anula en \(x=0\) y \(x=p\), luego tendrá su vértice (máximo) en \(x=\frac{p}{2}\). Deducimos así que hay romper el diamante en dos partes iguales para que la depreciación sea máxima.
Este fue el problema 7 de la fase nacional de la Olimpiada Matemática española de 1976.
Problema 28 (nivel 1) (propuesto el 30-1-2025) Se tienen 2024 bolas, en cada una de las cuales hay escrito un entero. Se cumple que siempre que formamos con ellas 1012 parejas hay dos parejas que tienen la misma suma. ¿Cuál es el mayor número de enteros distintos que puede haber entre todas las bolas?
SoluciónSolución. Veamos que la solución es 1011. Por un lado, si tenemos 1012 o más valores distintos, podemos formar una sucesión de 1012 bolas con valores \(x_1\lt x_2\lt\ldots\lt x_{1012}\) y ordenar las 1012 bolas restantes como \(y_1\leq y_2\leq\ldots\leq y_{1012}\). Entonces, emparejando cada \(x_k\) con \(y_k\), obtenemos 1012 parejas, cada una de las cuales tiene suma distinta. Por otro lado, sí hay ejemplos con sólo 1011 valores, como puede ser cuando tenemos 1010 bolas numeradas del 2 al 1011 y las otras 1012 numeradas con el 1. Hagamos como hagamos las parejas, siempre habrá dos de ellas formadas únicamente por unos y tendrán ambas suma 2.
Este problema está basado en el problema 11 de la Fase Local de la Olimpiada Matemática Española de 2015.
Problema 27 (nivel 1) (propuesto el 30-1-2025) De entre todos los triángulos que tienen un lado igual a 5 y el ángulo opuesto de \(30^\circ\), determinar el de área máxima, calculando el valor de los otros dos ángulos y el área del triángulo.
SoluciónSolución. Pongamos que \(AB=5\), luego el vértice \(C\) tiene que estar sobre el arco mayor de una circunferencia que fija pasa por \(AB\) formada por los puntos del plano que ven \(AB\) bajo un ángulo de \(30^\circ\) (propiedad del arco capaz). Si medimos el área como la mitad de la base por la altura, esta será máxima cuando \(C\) esté lo más distante posible de la recta que pasa por \(A\) y \(B\), lo que nos lleva a que \(C\) está en la intersección de la mediatriz del segmento \(AB\) con la circunferencia, es decir, cuando el triángulo es isósceles. Tiene, por tanto, los otros dos ángulos iguales e iguales a \(75^\circ\). La altura del triángulo se puede calcular como \(h=\frac{5}{2}\tan(75^\circ)=\frac{5}{2}(2+\sqrt{3})\), luego el área estará dada por \(S=\frac{1}{2}AB\cdot h=\frac{25}{4}(2+\sqrt{3})\).
Observa que podemos calcular \(\tan(75^\circ)\) usando las fórmulas trigonométricas para el ángulo mitad (¿sabrías completar los cálculos?): \[\tan(75^\circ)=\frac{\mathrm{sen}(75^\circ)}{\cos(75^\circ)}=\frac{\cos(15^\circ)}{\mathrm{sen}(15^\circ)}=\sqrt{\frac{1+\cos(30^\circ)}{1-\cos(30^\circ)}}\]
Este fue el problema 1 de la Fase Nacional de la Olimpiada Matemática Española de 1980.
Problema 26 (nivel 1) (propuesto el 23-1-2025) En cada casilla de un tablero \(m\times n\) se encuentra un número real. Se permite cambiar todos los números de una fila o de una columna de signo tantas veces como queramos. Demostrar que puede conseguirse que las sumas de los elementos cada fila y cada columna sean no negativas independientemente de la configuración inicial.
SoluciónSolución. Sea \(S\) la suma total de los elementos de la tabla. Cada vez que nos encontremos una fila o columna con suma negativa la cambiamos de signo. Cada una de estas operaciones incrementa el valor de \(S\) y, como hay un número limitado de combinaciones de signos (es menor o igual que \(2^{mn}\), el número de elecciones de signos \(\pm\) en los \(mn\) elementos de la tabla), este proceso no puede continuar indefinidamente, es decir, llegamos a un punto en el que todas las filas y columnas tienen suma positiva.
Problema 25 (nivel 1) (propuesto el 23-1-2025) Encontrar todas las aplicaciones \(f:\mathbb{Z}\to\mathbb{Z}\) que verifican \[f(n)+f(n+1)=2n+1\] para cualquier entero \(n\) y además \(f(1)+f(2)+\ldots+f(63)=2015\).
SoluciónSolución. Cambiando \(n\) por \(n+1\) obtenemos la igualdad \(f(n+1)+f(n+2)=2n+3\). Si a esta le restamos la ecuación del enunciado, obtenemos que \(f(n+2)=f(n)+2\) para todo entero \(n\). De aquí se deduce fácilmente por inducción sobre \(k\) que \[f(2k)=2k+f(0),\qquad f(2k+1)=2k+f(1).\] Por tanto, \(a=f(0)\) y \(b=f(1)\) determinan completamente a la función y verifican \(a+b=1\) (haciendo \(n=0\) en la ecuación funcional original). Si imponemos la otra condición del enunciado, tenemos que \begin{align*} 2015&=f(1)+f(2)+\ldots+f(63)\\&=31a+2+4+\ldots+62+32b+2+4+\ldots+62\\ &=31a+32b+2(1+2+\ldots+31)\\&=31a+32b+31\cdot 32=31a+32b+992. \end{align*} Por tanto, tenemos el sistema de ecuaciones \[\left\{\begin{array}{l}a+b=1\\31a+32b=1023\end{array}\right.\] que se resuelve fácilmente dando la solución única \(a=-991\) y \(b=992\). Deducimos así que solo existe una función cumpliendo las condiciones dadas y está definida por \[f(n)=\begin{cases}n-991&\text{si }n\text{ par},\\n+991&\text{si }n\text{ impar}.\end{cases}\]
Este fue el problema 10 de la fase local de la Olimpiada Matemática Española de 2015.
Problema 24 (nivel 2) (propuesto el 16-1-2025) Demostrar que para cada número natural \(k\) existe un número \(n\) con más de \(k\) dígitos que simultáneamente las siguientes condiciones:
- Todos los dígitos de \(n\) son mayores que \(1\).
- Siempre que se multipliquen cuatro dígitos de \(n\) se obtiene un d ivisor de \(n\).
SoluciónSolución. Como \(10\) es primo relativo con \(9^4\), el teorema de Euler nos asegura que \(n=\varphi(9^4)=\varphi(3^8)=2\cdot 3^7\) verifica que \(10^n\equiv 1\ (\mathrm{mod}\ 9^4)\). Entonces, \(10^n-1\) es un número formado únicamente por nueves que es múltiplo de \(9^4\), luego es charrúa. También es charrúa el número \(10^{bn}-1\) para todo entero positivo \(b\) ya que \(10^{bn}=(10^{n})^b\equiv 1^b=1\ (\mathrm{mod}\9^4)\). Como \(10^{bn}-1\) tiene \(bn\) dígitos, obtenemos de este modo números charrúas con tantos dígitos como queramos.
Este fue el problema 1 de la Olimpiada Iberoamericana de Matemáticas de 2001.
Problema 23 (nivel 1) (propuesto el 16-1-2025) Dos jugadores A y B y otras 2001 personas forman un círculo, de modo que A y B no quedan en posiciones consecutivas. A y B juegan por turnos alternadamente empezando por A. Una jugada consiste en tocar a una de las personas que se encuentran a su lado, la cual debe salir del círculo. Gana el jugador que logre sacar del círculo a su oponente. Demostrar que uno de los dos jugadores tiene una estrategia ganadora y describir dicha estrategia.
SoluciónSolución. Como hay un número impar de jugadores, en uno de los dos arcos de extremos A y B habrá un número par de personas y en el otro un número impar. El primer jugador A tiene una estrategia ganadora que consiste en eliminar primero una persona del arco que tiene un número par para dejar los dos con una cantidad impar de personas. A partir de ahí, A sólo tiene que copiar el arco que ha elegido B en su turno. Esto le garantiza que siempre queda un número impar de personas en cada arco tras su jugada; en particular, no quedan cero personas y B no puede ganar en su turno siguiente. El primer jugador que deja un arco con ninguna persona es B y en su siguiente turno A lo elimina.
Este fue el problema 1 de la Olimpiada Matemática de Centroamérica y El Caribe de 2001.
Problema 22 (nivel 2) (propuesto el 9-1-2025) El ángulo \(A\) del triángulo isósceles \(ABC\) mide \(36^\circ\), siendo iguales sus ángulos \(B\) y \(C\). La bisectriz de su ángulo \(C\) corta al lado opuesto en el punto \(D\).
- Calcular las medidas de los ángulos del triángulo \(BCD\).
- Expresar la medida del lado \(BC\) en función de la medida del lado \(AC\), sin que en la expresión aparezcan razones trigonométricas.
SoluciónSolución. Por ser el triángulo isósceles, tenemos que \(\angle ABC=\angle ACB=\frac{180-36}{2}=72^\circ\). La bisectriz divide al ángulo en dos ángulos iguales, luego \(\angle ABD=\angle DBC=\frac{72}{2}=36^\circ\). Además, como la suma de los ángulos de \(BCD\) es \(180^\circ\), obtenemos rápidamente \(\angle BDC=180-36-72=72\). Por tanto, el triángulo \(BCD\) es isósceles y tiene ángulos de \(36^\circ, 72^\circ, 72^\circ\).
El triángulo \(ABD\) también es isósceles por tener dos ángulos iguales a \(36^\circ\), luego \(BC=BD=AD\). Además, \(BCD\) y \(ABC\) son semejantes por tener los ángulos iguales, luego \[\frac{AC}{BC}=\frac{BC}{CD}=\frac{BC}{AC-AD}=\frac{BC}{AC-BC}.\] De esta igualdad, obtenemos que \(AC^2-AC\cdot BC-BC^2=0\). Dividiendo entre \(AC^2\), llegamos a la ecuación de segundo grado \[\left(\frac{BC}{AC}\right)^2+\frac{BC}{AC}-1=0\ \Longrightarrow\ \frac{BC}{AC}=\frac{-1\pm\sqrt{5}}{2}.\] Tenemos que descartar la solución negativa, lo que nos dice finalmente que \[BC=\frac{\sqrt{5}-1}{2}AC.\]
Este fue el problema 4 de la fase nacional de la Olimpiada Matemática Española de 2004.
Problema 21 (nivel 2) (propuesto el 9-1-2025) Un jardinero tiene que plantar en una fila a lo largo de un camino tres robles, cuatro encinas y cinco hayas. Planta los árboles al azar siendo la probabilidad de plantar un árbol u otro la misma. Halla la probabilidad de que, una vez plantados todos los árboles, no haya dos hayas consecutivas.
SoluciónSolución. Vamos a poner que el jardinero tiene los \(12\) árboles en macetas y va cogiendo una a una una maceta sin mirar de qué tipo de árbol es y las plantas consecutivamente en \(12\) agujeros que previamente ha cavado. De esta forma, está claro que hay \(12!\) formas posibles de plantar los árboles. Veamos cuántas de ellas tienen no tienen hayas consecutivas para hallar la probabilidad como
casos favorables entre casos posibles
.
Si escribimos \(H\) para indicar las hayas y \(A\) para los otros árboles (robles o encinas), para que las hayas no queden consecutivas, tendremos que poner al menos un árbol entre cada haya:\[\_\ H\ A\ \_\ H\ A\ \_\ H\ A\ \_\ H\ A\ \_\ H\ \_\]aunque nos quedan seis huecos marcados con \(\_\) para poner otras tres \(A\). Estas se podrán poner libremente en uno de los seis huecos, lo que nos da un total de \(6^3\) configuraciones. Para cada una de ellas, podemos permutar las \(H\) y permutar las \(A\) libremente, lo que nos da un total de \(5!\cdot 7!\) casos posibles por cada una de las \(6^3\) configuraciones. La probabilidad que buscamos es, por lo tanto, \[\frac{6^3\cdot 5!\cdot 7!}{12!}=\frac{3}{11}.\]
Este fue el problema 10 de la fase local de la Olimpiada Matemática Española de 2010.
Problema 20 (nivel 1) (propuesto el 2-1-2025) Hallar todos los números enteros positivos que son menores que 1000 tales que el cubo de la suma de sus cifras es igual al cuadrado del dicho entero.
SoluciónSolución. Un número que cumpla dicha condición cumple que su cuadrado es un cubo perfecto luego el número en sí ha de ser un cubo perfecto (todos los exponentes en su descomposición de su cuadrado en factores primos han de ser múltiplos de 3 luego los del propio número también). Como tiene que ser menor que 1000, tenemos las posibilidades 1, 8, 27, 64, 125, 216, 343, 512 y 729. Además, por el mismo motivo, la suma de sus cifras ha de ser un cuadrado perfecto luego de estos nos quedan 1, 27 y 216, de los cuales sólo 1 y 27 cumplen la condición buscada.
Este fue el problema 1 de la Olimpiada Iberoamericana de Matemáticas de 1999.
Problema 19 (nivel 2) (propuesto el 2-1-2025) Tenemos \(n\) puntos en el plano, algunos de los cuales están conectados por segmentos que no se cortan entre sí. Sabemos además que se puede viajar entre cualesquiera dos puntos moviéndonos a lo largo de los segmentos y sólo hay una forma de viajar entre dichos puntos. Demostrar que el número total de segmentos es \(n-1\).
Indicación: usar inducción sobre \(n\).
SoluciónSolución. Procedamos por inducción sobre \(n\). El caso base es \(n=2\), en cuyo caso hay necesariamente dos puntos unidos por \(n-1=1\) segmentos y no hay nada que probar. Supongamos entonces que el enunciado es cierto tal cual está escrito para \(n\) puntos y veamos lo que pasa si tenemos \(n+1\) puntos con dicha propiedad. Al hacer un camino a lo largo de los segmentos sin repetir segmento, como no podemos volver a ningún punto ya visitado (habría dos caminos distintos con el mismo origen y el mismo final), llegará un momento en que no podremos seguir y habremos alcanzado un punto \(p_0\) al que solo llega un segmento (mediante el cual hemos accedido a \(p_0\)). Si eliminamos \(p_0\) y dicho segmento, tendremos \(n\) puntos que verifican la misma propiedad, luego la hipótesis de inducción nos asegura que el número de segmentos es \(n-1\). Añadiendo el que hemos eliminado, deducimos que el número de segmentos para \(n+1\) puntos es \(n\), como queríamos probar.
Este problema apareció en una olimpiada soviética de 1962.
Problema 18 (nivel 1) (propuesto el 26-12-2024) Un año es bisiesto si es múltiplo de 4 pero no múltiplo de 100, excepto que sea múltiplo de 400. Por ejemplo, 1984, 2000 y 2012 son años bisiestos, mientras que 1900 no lo es. Consideremos un día cualquiera del año, distinto del 29 de febrero. Demostrar que los días de la semana (lunes, martes,...) en que puede caer dicho día no son equiprobables (cuando se toma un año al azar).
SoluciónSolución. El ciclo de bisiestos dura 400 años, período en el que hay 97 años bisiestos. Esto supone un total de \(400\cdot 365+97=146097=7\cdot 20871\) días en este período. Como es un múltiplo de 7, cada 400 años se repite el calendario, luego podemos suponer que elegimos un día y trabajar en un período concreto de 400 años sin perder generalidad. Ese día ocurre 400 veces en esos 400 años, pero 400 no es múltiplo de 7, luego cada día de la semana no puede ser equiprobable.
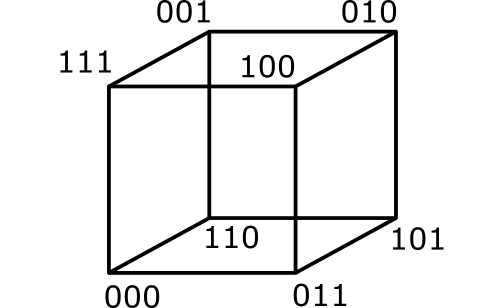
Problema 17 (nivel 1) (propuesto el 26-12-2024) ¿Se pueden etiquetar los ocho vértices de un cubo con los números de tres dígitos en binario (del 000 al 111) sin repetir ninguno y de forma que dos vértices adyacentes difieran en al menos dos de los dígitos?
SoluciónSolución. Sí se puede:
Problema 16 (nivel 1) (propuesto el 19-12-2024) ¿Es posible dibujar 2003 segmentos en el plano de forma que cada uno de ellos corte exactamente a otros tres segmentos?
SoluciónSolución. Por reducción al absurdo, si cada segmento cortara a otros tres, el número \(2025\cdot 3\) sería el doble del número de puntos de corte (ya que cada uno lo estaríamos contando dos veces), pero este número es impar, lo cual es una contradicción.
Este fue con un pequeño cambio, el problema 3 de la fase local de la Olimpiada Matemática Española de 2003.
Problema 15 (nivel 1) (propuesto el 19-12-2024) Dado un entero positivo \(n\) escrito en el sistema de numeración decimal, formamos el número entero \(k\) restando del número formado por las tres últimas cifras de \(n\) el numero formado por las cifras anteriores restantes. (por ejemplo, si \(n=3486411\), entonces \(k=411-3486=-3075\)). Demostrar que \(n\) es divisible por 7, 11 o 13 si, y solo si, lo es \(k\).
SoluciónSolución. Podemos expresar \(n=1000a+b\) para ciertos enteros \(a\) y \(b\) con \(0\leq b\leq 999\) es el número que representa las tres últimas cifras de \(n\) y \(a\) las cifras restantes. Entonces, tenemos que \[k=b-a=n-1000a-a=n-1001a=n-7\cdot 11\cdot 13a.\] Esto nos dice que si 7, 11 o 13 dividen a \(n\), el miembro de la derecha será múltiplo de este factor, luego \(k\) también lo será. Análogamente, si despejamos \(n=k+7\cdot 11\cdot 13a\), tenemos que si \(k\) es múltiplo de 7, 11 o 13, también lo será \(n\).
Este fue, con un pequeño cambio, el problema 7 de la fase local de la Olimpiada Matemática Española de 2013.
Problema 14 (nivel 1) (propuesto el 12-12-2024) Un número positivo \(x\) verifica la ecuación \(x^2+\frac{1}{x^2}=7\). Demostrar que el número \[x^5+\frac{1}{x^5}\] es entero y calcularlo.
SoluciónSolución. Desarrollamos \[\left(x+\tfrac{1}{x}\right)^2=x^2+2+\frac{1}{x^2}=2+7=9,\] por lo que se tiene que \(x+\frac{1}{x}=3\) (por ser \(x\) positivo). Vamos entonces calcular otras potencias de \(x+\frac{1}{x}\) utilizando el binomio de Newton. Por un lado, tenemos que \[27=\left(x+\tfrac{1}{x}\right)^3=x^3+3x+\tfrac{3}{x}+\tfrac{1}{x^3}=\left(x^3+\tfrac{1}{x^3}\right)+3\left(x+\tfrac{1}{x}\right)\] nos permite despejar \(x^3+\frac{1}{x^3}=27-3\cdot 3=18\). Por otro lado, de \begin{align*} 243=3^5=\left(x+\tfrac{1}{x}\right)^5&=x^5+5x^3+10x+\tfrac{10}{x}+\tfrac{5}{x^3}+\tfrac{1}{x^5}\\&=\left(x^5+\tfrac{1}{x^5}\right)+5\left(x^3+\tfrac{1}{x^3}\right)+10\left(x+\tfrac{1}{x}\right)\end{align*} podemos despejar \(x^5+\tfrac{1}{x^5}=243-5\cdot 18-10\cdot 3=123\).
Este fue el problema 5 de la fase local de la Olimpiada Matemática Española de 2006.
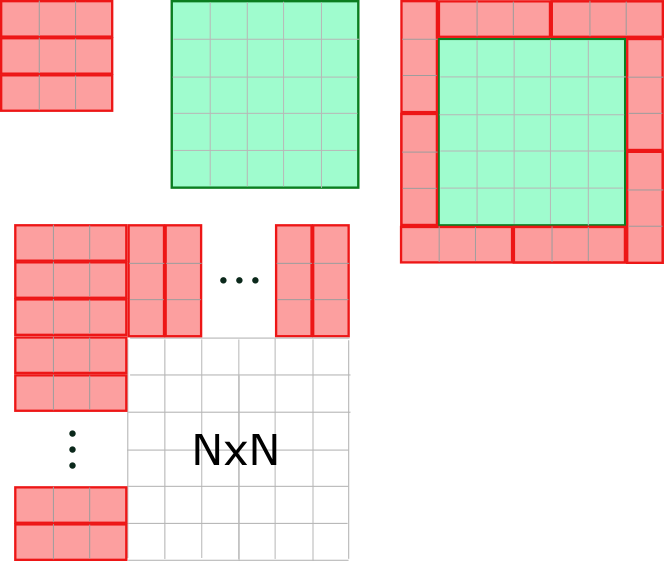
Problema 13 (nivel 1) (propuesto el 12-12-2024) Encontrar todos los números naturales \(N\) para los que un tablero \(N\times N\) se puede recubrir con piezas de tamaño \(5\times 5\) y piezas de tamaño \(1\times 3\).
SoluciónSolución. Comenzamos observando que los tableros \(3\times 3\) y \(5\times 5\) se pueden recubrir fácilmente y tampoco es difícil dar con un recubrimiento del tablero \(7\times 7\), como se muestra en la figura. Además, dado un tablero \(\times N\) que se pueda recubrir, también se puede recubrir uno de dimensiones \((N+3)\times(N+3)\) pues basta con rodearlo rellenar las columnas nuevas con fichas \(1\times 3\) todas orientadas en horizontal y las casillas restantes de las tres filas nuevas con fichas \(3\times 1\) todas en vertical (como se muestra en la figura de abajo). Esto nos deja solo por comprobar los tableros de tamaño \(1\times 1\), \(2\times 2\) y \(4\times 4\), que claramente no se pueden recubrir ya que el número de casillas es menor de 25 y no es múltiplo de 3.
Este fue el problema 4 de la Olimpiada Matemática de Centroamérica y el Caribe de 2010.
Problema 12 (nivel 1) (propuesto el 5-12-2024) Sean \(a\), \(b\) y \(c\) números reales. Probar que, si \(x^3+ax^2+bx+c\) tiene tres raíces reales, entonces \(3b\leq a^2\).
SoluciónSolución. Escribamos las tres raíces como \(\alpha,\beta,\gamma\in\mathbb{R}\). Desarrollando \[(x-\alpha)(x-\beta)(x-\gamma)=x^3-(\alpha+\beta+\gamma)x^2+(\alpha\beta+\beta\gamma+\gamma\alpha)x-\alpha\beta\gamma,\] podemos identificar coeficientes para obtener las relaciones de Cardano-Vieta \(a=-(\alpha+\beta+\gamma)\) y \(b=\alpha\beta+\beta\gamma+\gamma\alpha\). Con esto podemos calcular \begin{align*}a^2-3b&=(\alpha+\beta+\gamma)^2-3(\alpha\beta+\beta\gamma+\gamma\alpha)\\&=\alpha^2+\beta^2+\gamma^2-\alpha\beta-\beta\gamma-\gamma\alpha\\&=\tfrac{1}{2}\left((\alpha-\beta)^2+(\beta-\gamma)^2+(\gamma-\alpha)^2\right)\geq 0.\end{align*}
Este fue el problema 4 de la fase local de la Olimpiada Matemática Española de 2001.
Problema 11 (nivel 1) (propuesto el 5-12-2024) Se tienen 2022 tarjetas numeradas dese 1 hasta 2022. Los números de las tarjetas son visibles todo el tiempo. Ana y Bárbara juegan tomando una tarjeta en cada turno hasta que se acaben, empezando por Ana. Cuando terminan de tomar todas las tarjetas, cada una suma los números de sus tarjetas y la que obtenga como resultado un número par gana el juego. Determinar qué jugadora tiene una estrategia para ganar siempre.
SoluciónSolución. Veamos una estrategia ganadora para Ana, la primera jugadora. En los números del 1 al 2022 hay 1011 números pares y 1011 impares, luego el quid de la cuestión es ver cuál de las dos jugadoras tiene al final un número impar de tarjetas impares. Lo que tiene que hacer Ana es elegir en primer lugar una tarjeta par y luego copiar la paridad de la tarjeta que haya elegido Bárbara. Esto garantiza que habrá un momento del juego en que Ana tenga 1004 tarjetas impares y Bárbara tenga 1005. Observa que, al tomar la primera tarjeta par, Ana se garantiza que no se pueda quedar sin elegir una tarjeta par cada vez que Bárbara lo haga.
Este fue, con una pequeña modificación, el problema 1 de la Olimpiada Matemática de Centroamérica y El Caribe de 2018.
Problema 10 (nivel 1) (propuesto el 28-11-2024) Encontrar todos los números naturales de tres dígitos tales que la suma de los cuadrados de los dígitos es un divisor de 26.
SoluciónSolución. Como \(26=2\cdot 13\), llegamos fácilmente a que los únicos divisores positivos de 26 son \(\{1,2,13,26\}\). Distingamos los cuatro casos:
- Si \(a^2+b^2+c^2=1\), entonces uno de los tres dígitos es igual a 1 y el resto a 0, lo que nos lleva a la única solución \((a,b,c)=(1,0,0)\) ya que debe ser \(a\neq 0\).
- Si \(a^2+b^2+c^2=2\), entonces dos de los tres dígitos son iguales a 1 y el tercero a 0, lo que nos da dos soluciones: \((a,b,c)=(1,1,0)\) y \((a,b,c)=(1,0,1)\), de nuevo porque \(a\neq 0\).
- Si \(a^2+b^2+c^2=13\), entonces los dígitos están entre 0 y 3, pero no pueden ser todos menores o iguales que 2 puesto que entonces \(a^2+b^2+c^2\leq 12\). Por tanto, uno de ellos es 3 y la suma de los cuadrados de los otros dos es 4, lo que lleva claramente a que sean 2 y 0. Tenemos así cuatro posibles soluciones: \((3,2,0)\), \((2,3,0)\), \((3,0,2)\) y \((2,0,3)\) ya que \(a\neq 0\).
- Finalmente, si \(a^2+b^2+c^2=26\), todos los dígitos están entre 0 y 5. Si uno de ellos es 5, los otros deben ser 1 y 0. Si uno de ellos es 4, los otros deben ser 3 y 1. Si el mayor es 3, entonces los cuadrados de los otros dos deben sumar 17, pero esto no es posible. Tampoco hay soluciones si el mayor es menor o igual que 2, como en el caso anterior.
En resumen, hemos encontrado los diecisiete números que cumplen la condición del enunciado: 100, 101, 105, 110, 134, 143, 150, 203, 230, 302, 314, 320, 341, 413, 431, 501 y 510.
Este fue el problema 1 de la Olimpiada Matemática de Centroamérica y El Caribe de 2000.
Problema 9 (nivel 2) (propuesto el 28-11-2024) Sea \(p(x)\) un polinomio con coeficientes enteros tal que \[p(2018)p(2019) = 2021.\] Probar que no hay ningún entero \(k\) tal que \(p(k) = 2020\).
Indicación: Utiliza que si \(a\) y \(b\) son enteros, entonces \(a-b\) divide a \(p(a)-p(b)\). ¿Sabrías demostrar esta propiedad? Solución
Solución. Supongamos por reducción al absurdo que \(k\) es un entero tal que \(p(k)=2020\). Entonces, tenemos que \[k-2018\text{ divide a }p(k)-p(2018)=2020-p(2018),\] \[k-2019\text{ divide a }p(k)-p(2019)=2020-p(2019),\] según la indicación. Como \(p(2018)\) y \(p(2019)\) son divisores de \(2021\), deben ser necesariamente números impares, luego \(2020-p(2018)\) y \(2020-p(2019)\) son números impares. Sin embargo, uno de los dos números \(k-2018\) o \(k-2019\) tiene que ser par. Como un número par no puede dividir a un impar, hemos encontrado la contradicción que buscábamos.
Este fue el problema 2 de la fase andaluza de la Olimpiada Matemática Española de 2021.
Problema 8 (nivel 1) (propuesto el 21-11-2024) En un triángulo escaleno \(ABC\) con \(\angle BAC=90^\circ\) se consideran las circunferencias inscrita y circunscrita. La recta tangente en \(A\) a la circunferencia circunscrita corta a la recta \(BC\) en \(M\). Sean \(S\) y \(R\) los puntos de tangencia de la circunferencia inscrita con los catetos \(AC\) y \(AB\), respectivamente. La recta \(RS\) corta a la recta \(BC\) en \(N\). Las retas \(AM\) y \(SR\) se cortan en \(U\). Demostrar que el triángulo \(UMN\) es isósceles.
SoluciónSolución. Llamamos \(\gamma=\angle ACB\) por comodidad y supongamos que \(AB\lt AC\) sin perder generalidad. Tenemos que \(\angle AOC=2\gamma\) por la propiedad del ángulo central. Como \(OA\) y \(AM\) son perpendiculares, para que los ángulos del triángulo \(AMO\) sumen \(180\), tiene que ser \(\angle AMO=90-2\gamma\), luego \(\angle NMU=90+2\gamma\) y ya tenemos uno de los tres ángulos del triángulo \(UMN\). Por otro lado, se tiene que \(ARS\) es rectángulo isósceles, luego \(\angle NRB=\angle ARS=45\). Como \(\angle RBN=180-\angle ABC=180-(90-\gamma)=90+\gamma\), para que los ángulos de \(NRB\) sumen \(180\) tiene que ser \(\angle RNB=45-\gamma\) y tenemos el segundo ángulo de \(UMN\). Para que la suma sea \(180\), el tercero tiene que ser igual a \(180-(90+2\gamma)-(45-\gamma)=45-\gamma\), luego \(\angle UNM=\angle MUN=45-\gamma\) y queda demostrado que el triángulo \(UMN\) es isósceles.
Este fue el problema 1 de la Olimpiada Iberoamericana de Matemáticas de 2006.
Problema 7 (nivel 2) (propuesto el 21-11-2024) Sean \(x,y\geq 0\) números reales tales que \(x+y=2\). Probar que \[x^2y^2(x^2+y^2)\leq 2.\]
SoluciónSolución. Sustituyendo \(x=1+t\) e \(y=1-t\) para cierto \(t\in[0,1]\), tenemos que\begin{align*}x^2y^2(x^2+y^2)&=(1+t)^2(1-t)^2((1+t)^2+(1-t)^2)\\&=2(1-t^2)^2(1+t^2)=2(1-t^2)(1-t^4)\leq 2,\end{align*} puesto que \(t^2\) y \(t^4\) son números reales entre \(0\) y \(1\).
Este fue el problema 1 de la fase andaluza de la Olimpiada Matemática Española de 2021.
Problema 6 (nivel 1) (propuesto el 14-11-2024) Hallar dos enteros positivos \(a\) y \(b\), tales que \(b^2\) sea múltiplo de \(a\), \(a^3\) sea múltiplo de \(b^2\), \(b^4\) sea múltiplo de \(a^3\) y \(a^5\) sea múltiplo de \(b^4\), pero de forma que \(b^6\) no sea múltiplo de \(a^5\).
SoluciónSolución. Consideremos un primo \(p\) y tomemos los números \(a=p^x\) y \(b=p^y\) para ciertos exponentes enteros positivos \(x\) e \(y\) aún por determinar. Las condiciones del enunciado se traducen como sigue: \begin{align*} b^2\text{ es múltiplo de }a&\ \Longleftrightarrow\ 2y\geq x,\\ a^3\text{ es múltiplo de }b^2&\ \Longleftrightarrow\ 3x\geq 2y,\\b^4\text{ es múltiplo de }a^3&\ \Longleftrightarrow\ 4y\geq 3x,\\a^5\text{ es múltiplo de }b^4&\ \Longleftrightarrow\ 5x\geq 4y,\\b^6\text{ no es múltiplo de }a^5&\ \Longleftrightarrow\ 6y\lt 5x.\end{align*}La primera y tercera desigualdades nos dicen que \(y\geq\frac{1}{2}x\) e \(y\geq\frac{3}{4}x\). Podemos quedarnos solamente con \(y\geq\frac{3}{4}x\) pues todo número que cumpla esta desigualdad también cumplirá la otra. Análogamente, la segunda, cuarta y quinta desigualdades nos dicen que \(y\leq\frac{3}{2}x\), \(y\leq\frac{5}{4}x\) e \(y\lt\frac{5}{6}x,\) de las cuales ahora la más restrictiva es \(y\lt\frac{5}{6}x\) y podemos eliminar las otras dos.
Todo esto nos dice que buscamos números \(x\) e \(y\) tales que \(\frac{3}{4}x\leq y\lt\frac{5}{6}x\) o, lo que es lo mismo, \(18x\leq 24y\lt 20x\). Hay muchas soluciones a esta desigualdad y solo buscamos una, por ejemplo, \(y=3\) y \(x=4\). Deducimos que los números \(a=p^4\) y \(b=p^3\) cumplen la condición del enunciado.
Este fue el problema 4 de la fase local de la Olimpiada Matemática Española de 2006.
Problema 5 (nivel 1) (propuesto el 14-11-2024) Se ordenan de menor a mayor los enteros positivos que pueden expresarse como suma de 2005 enteros consecutivos, no necesariamente positivos. ¿Cuál ocupa la posición 2005?
SoluciónSolución. Pongamos que los 2005 enteros consecutivos son \[n-1002,n-1001,\ldots,n-1,n,n+1,\ldots,n+1002.\] Al sumarlos todos queda \(2005n\) ya que se cancelan sumandos por parejas (el primero con el último, el segundo con el penúltimo y así sucesivamente) de forma que la suma equivale a sumar \(2005\) veces el número central \(n\). Vemos así que los números que se expresan de esta forma son los múltiplos de 2005. El que ocupa la posición 2005 de entre aquellos que son positivos es claramente \(2005\cdot 2005=2005^2\).
Este fue el problema 1 en la Olimpiada Matemática de Centroamérica y El Caribe de 2005.
Problema 4 (nivel 2) (propuesto el 7-11-2024) Al cortar un tetraedro regular con un cierto plano se obtiene como sección un paralelogramo. Demostrar que este paralelogramo debe ser necesariamente un rectángulo.
SoluciónSolución. Sea \(ABCD\) el tetraedro regular. Para que la sección producida sea un cuadrilátero y no un triángulo, el plano debe dejar a cada lado dos de los vértices: supondremos que \(A\) y \(B\) están a un lado y \(C\) y \(D\) al otro, de forma que el paralelogramo \(PQRS\) tiene los vértices \(P,Q,R,S\) sobre los lados del tetraedro \(BD,DA,AC,CB\), respectivamente. Por ser paralelogramo, la recta \(QR\) es paralela a \(PS\) y admiten un vector director común \(\vec u\) que debe ser paralelo a los planos que contienen las caras \(ACD\) y \(BCD\) y, por tanto, la recta \(CD\), intersección de estos dos planos, tiene que tener también a \(\vec u\) por vector director (en otras palabras, \(PS\) y \(QR\) son paralelas a \(CD\)). Del mismo modo se demuestra que \(RS\) y \(PQ\) tienen por vector director al vector director de \(AB\), que llamaremos \(\vec v\). Como \(\vec u\) y \(\vec v\) son perpendiculares (las rectas \(AB\) y \(CD\) se cruzan en el espacio de forma perpendicular por las simetrías del tetraedro), se sigue \(PQRS\) tiene todos sus ángulos iguales a \(90^\circ\) y, en consecuencia, se trata de un rectángulo.
Este fue esencialmente el problema 2 de la fase local de la Olimpiada Matemática Española de 2009.
Problema 3 (nivel 1) (propuesto el 7-11-2024) Cada número natural se colorea de azul o de rojo, de modo que, si \(x\) e \(y\) están pintados del mismo color, entonces \(x+y\) está pintado de azul (observar que podría ser \(x=y\)). Determinar todas las formas de colorear los números naturales que sigan esta regla.
SoluciónSolución. Los números pares son de la forma \(2k\) y tienen que ser necesariamente azules ya que se obtienen como suma de un número consigo mismo, es decir, \(2k=k+k\). Los números impares son de la forma \(2k+1\) y si uno está pintado de azul, todos los siguientes impares \(2k+3=(2k+1)+2\), \(2k+5=(2k+1)+4\), \(2k+7=(2k+1)+6\),... también tienen que estar pintados de azul. Nos quedan, en consecuencia, las siguientes posibles coloraciones:
- Todos los pares de azul y todos los impares de rojo.
- Todos los enteros de azul salvo los primeros \(n\) impares, que están pintados de rojo, para cierto \(n\geq 0\). En particular, para \(n=0\), tendríamos todos los enteros pintados de azul.
Es fácil ver que estas dos formas de pintar cumplen la regla de coloración, luego son las únicas posibilidades.
Este fue el problema 1 de la Olimpiada Matemática de Centroamérica y El Caribe de 2023.
Problema 2 (nivel 1) (propuesto el 31-10-2024) Se tienen 2024 números reales tales que la suma de 500 cualesquiera de ellos es positiva. ¿Es la suma de todos los números necesariamente positiva? ¿Son necesariamente todos positivos?
SoluciónSolución. La respuesta a la primera pregunta es que sí. Para probarlo, la idea es que si los números son \(a_1,a_2,\ldots,a_{2024}\), podemos considerar la suma \(S_n\) de los números desde el \(a_n\) hasta el \(a_{n+499}\) de forma que cuando nos pasemos de \(a_{2024}\) seguimos por \(a_1\) (esto suele explicarse diciendo que consideramos los números ordenados cíclicamente o bien definiendo \(a_{2024+k}=a_k\) para todo \(k\geq 1\)). De esta forma, si sumamos todas las sumas \(S_1,S_2,\ldots,S_{2024}\), cada uno de los números originales aparece en 500 de ellas, luego se cumple que \[0\lt S_1+S_2+\ldots+S_{2024}=500 S,\] siendo \(S\) la suma de los 2024 números. De aquí deducimos que \(S\gt 0\).
Sin embargo, no tienen por qué ser todos los números positivos ya que podrían ser, por ejemplo, \(499\) de ellos iguales a \(-1\) y el resto iguales a \(500\).
Este fue, con algunas modificaciones, el problema 2 de la fase local de la Olimpiada Matemática Española de 2020.
Problema 1 (nivel 1) (propuesto el 31-10-2024) Hallar todas las soluciones enteras de la ecuación \[x^4+y^4=2024x^3y.\]
SoluciónSolución. Supongamos que los enteros \(x\) e \(y\) cumplen la ecuación y que ninguno de ellos es cero (si uno fuese cero, el otro también lo sería y tendríamos la solución \(x=y=0\)). Si \(d\) es el máximo común divisor común de \(x\) e \(y\), podemos dividir la ecuación por \(d^4\) y obtenemos que \[\left(\frac{x}{d}\right)^4+\left(\frac{y}{d}\right)^4=2024\left(\frac{x}{d}\right)^3\left(\frac{y}{d}\right),\] es decir, \(u=\frac{x}{d}\) y \(v=\frac{y}{d}\) son no nulos, también la cumplen la ecuación y no tienen divisores comunes. Ahora bien, si \(p\) es un primo que divide a \(u\), entonces \(v^4=2024u^3v-u^4\) también es divisible por \(p\), luego \(v\) es divisible por \(p\). Esto nos dice que ningún primo puede dividir a \(u\) ya que sería un factor común con \(v\) y hemos visto que no tienen factores comunes. De la misma forma, se demuestra que ningún primo puede dividir a \(v\) y, por tanto, \(u\) y \(v\) tienen que ser iguales a \(1\) o \(-1\). Sin embargo, si sustituimos estos valores en la ecuación original, no son soluciones. Deducimos así que la ecuación no tiene ninguna solución en los enteros salvo \(x=y=0\).
Este fue, con una pequeña modificación, el problema 5 de la fase local de la Olimpiada Matemática Española de 2014.




