Listado de ideas para la preparación
En un triángulo, ninguno de los tres lados mide más que la suma de los otros dos, es decir, si \(a,b,c\) son las longitudes de dichos lados, entonces se cumplen las desigualdades \[a\lt b+c,\qquad b\lt a+c,\qquad c\lt a+b.\] Ejercicio 1. Demuestra que la línea poligonal de menor longitud que une dos puntos del plano es el segmento de recta que los une. Ejercicio 2. Demuestra que, para cualesquiera números reales \(x_1,x_2,\ldots,x_n\) se cumple que\[|x_1+x_2+\ldtos+x_n|\leq|x_1|+|x_2|+\ldots+|x_n|.\] Ejercicio 3. ¿Cuántos triángulos distintos tienen perímetro 2024 y lados de longitudes enteras? Ejercicio 4. Sean \(a,b,c\) los lados de un triángulo. Demostrar que\[\frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b}\lt 2. Ejercicio 5. Dados puntos \(P_1,P_2,\ldots,P_n\) sobre una circunferencia de radio $1$, demostrar que hay un punto $X$ también en la misma circunferencia y tal que\[XP_1+XP_2+\ldots+XP_n\geq n.\]
La desigualdad de Jensen se aplica a una función convexa \(f:I\to\mathbb{R}\), siendo \(I\) un cierto intervalo de números reales. Concretamente, si \(x_1,x_2,\ldots,x_n\in I\) y \(w_1,w_2,\ldots,w_n\geq 0\) verfican \(w_1+w_2+\ldots+w_n=1\), entonces \[f(w_1x_1+w_2x_2+\ldots+w_nx_n)\leq w_1f(x_1)+w_2f(x_2)+\ldots+w_n f(x_n).\] Ejemplos de funciones convexas son \(f(x)=x^a\) y \(f(x)=a^x\) para \(a\gt 1\). En el caso de que la función sea cóncava, la desigualdad de Jensen va en la dirección contraria, como por ejemplo en el caso del logaritmo \(f(x)=\ln(x)\). En particular, la desigualdad de Jensen en ocasiones permite tratar desigualdades en las que aparecen funciones que no son polinómicas o racionales.
Si la función \(f(x)\) es estrictamente convexa, entonces la igualdad se alcanza si, y sólo si, \(x_1=x_2=\ldots=x_n\) o bien todos los pesos \(w_i\) son nulos salvo uno.
Ejercicio 1. Para \(n=2\), la desigualdad de Jensen nos dice que la gráfica de una función convexa se queda por debajo del segmento que une dos de sus puntos (y por encima en el caso de una función cóncava). Justifica estas afirmaciones. Ejercicio 2. Demuestra la desigualdad entre las medias aritmética y geométrica usando la desigualdad de Jensen para \(f(x)=\ln(x)\) con pesos \(x_1=x_2=\ldots=x_n=\frac{1}{n}\). Ejercicio 3. Haz lo mismo para la desigualdad entre las medias aritmética y cuadrática buscando tú la función idónea. Ejercicio 4. Demuestra que en un triángulo que tiene ángulos \(\alpha,\beta,\gamma\), se cumple que \[\mathrm{sen}(\alpha)+\mathrm{sen}(\beta)+\mathrm{sen}(\gamma)\leq\frac{3\sqrt{3}}{2}.\] Ejercicio 5. Demuestra que la función \(f(x)=\frac{1}{1+x^2}\) es convexa para \(x\geq\frac{1}{\sqrt{3}}\) y usa este resultado para demostrar que \[\frac{1}{1+x_1^2}+\frac{1}{1+x_2^2}+\ldots+\frac{1}{1+x_n^2}\geq \frac{n}{2}\]para cualesquiera números reales \(x_1,x_2,\ldots,x_n\geq\frac{1}{\sqrt{3}}\) tales que \(x_1+\ldots+x_n=n\). ¿Cuándo se alcanza la igualdad?El teorema chino del resto nos dice que si \(m\) y \(n\) son enteros primos entre sí y conocemos los restos de dividir un número \(a\) entre \(m\) y \(n\), entonces también sabemos el resto de dividir \(a\) entre su producto \(mn\). Escrito con congruencias, podemos decir que el sistema de congruencias\[\left\{\begin{array}{l}a\equiv r\ (\text{mod }m)\\a\equiv s\ (\text{mod }n)\end{array}\right.\]se puede expresar como una única congruencia \(a\equiv t\ (\text{mod }mn)\). Hay formas de calcular el nuevo resto \(t\) fácilmente. Por ejemplo, podemos usar la identidad de Bézout para encontrar enteros \(u,v\) tales que \(um+vn=1\) y luego tomar \(t=ums+vnr\). El teorema chino del resto también se puede aplicar a más de dos ecuaciones en congruencias si las vamos trabajando de dos en dos. Ejercicio 1. (a) Si un número deja resto \(3\) al dividirlo entre \(11\), ¿cuáles son sus posibles restos al dividirlo entre \(143\)? (b) Si un número deja resto \(8\) al dividirlo entre \(13\), ¿cuáles son sus posibles restos módulo \(143\)? (c) Combina los cálculos anteriores para hallar el resto de dividir entre \(143\) un número del que sabamos que deja resto \(3\) al dividirlo entre \(11\) y también resto \(8\) al dividirlo entre \(13\). Ejercicio 2. Justificar por qué en el problema arriba propuesto \(t=ums+vnr\) es una solución. Justificar por qué no puede haber más de una solución al sistema de ecuaciones módulo \(mn\). Ejercicio 3. Encuentra el menor entero positivo que deja resto 1 al dividirlo por 2, resto 2 al dividirlo por 3, resto 4 al dividirlo por 5 y resto 6 al dividirlo por 7. Ejercicio 4. Halla el resto de dividir \(7^{100}\) entre \(660\).
Supongamos que \(ABC\) es un triángulo cualquiera y llamemos \(a,b,c\) a sus lados y \(A,B,C\) a los ángulos opuestos, como es usual. El teorema del coseno nos da las siguientes igualdades, que generalizan al teorema de Pitágoras\begin{align*}a^2&=b^2+c^2-2bc\cos(A),\\b^2&=a^2+c^2-2ac\cos(B),\\c^2&=a^2+b^2-2ab\cos(C).\end{align*}Estas igualdades permiten, por ejemplo, calcular cualquier ángulo a partir de la longitud de los lados. Por su parte, el teorema del seno nos da las relaciones\[\frac{\mathrm{sen}(A)}{a}=\frac{\mathrm{sen}(A)}{a}=\frac{\mathrm{sen}(A)}{a}=\frac{1}{2R},\]donde \(R\) es el radio de la circunferencia circunscrita. Ejercicio 1. Si un triángulo tiene lados de longitudes \(3,5,7\), ¿cuál es el radio de su circunferencia circunscrita? Ejercicio 2. En un triángulo, la longitud de un lado es la media aritmética de las longitudes de los otros dos. Halla el máximo valor posible del ángulo opuesto a dicho lado. Ejercicio 3. En un triángulo \(ABC\) se toma un punto \(D\) sobre el lado \(AC\). Sabiendo que \(\angle ABC=90^\circ\), \(\angle DBC=30^\circ\) y \(AB=CD=1\), encontrar el valor de \(AD\). Ejercicio 4. Demuestra que en un triángulo \(ABC\), la bisectriz del ángulo \(A\) corta al lado \(BC\) en el punto \(D\). Demuestra que \[AD=\frac{\sqrt{bc(a+b+c)(-a+b+c)}}{b+c}.\]¿Cuáles son las fórmulas para las otras bisectrices? Ejercicio 5. En un triángulo \(ABC\), demuestra la desigualdad \[\frac{\cos(A)}{a^3}+\frac{\cos(B)}{b^3}+\frac{\cos(C)}{c^3}\geq\frac{3}{2abc}.\]
A la hora de buscar soluciones reales de una ecuación, un truco fenomenal es deducir otra ecuación de la forma \(A\cdot B=0\), ya que esto nos dice que \(A=0\) o bien \(B=0\). Ahora bien, si estamos buscando soluciones enteras, podemos intentar deducir otra ecuación de la forma \(A\cdot B=n\), siendo \(n\) un entero, pues en tal caso, \(A\) y \(B\) serán divisores complementarios de \(n\). Esto nos da siempre un número finito de posibilidades (¡hay que tener cuidado con no olvidar que los divisores pueden ser positivos o negativos!). Ejercicio 1. Encuentra todos los enteros \(n\) tales que \(n\) y \(n+25\) son ambos cuadrados perfectos. Ejercicio 2. Encuentra todas las soluciones enteras de la ecuación \(xy=27+2(x+y)\). Haz lo mismo para la ecuación \(7xy=3x+4y\). Ejercicio 3. Encontrar un primo \(p\) sabiendo que \(71p+1\) es un cuadrado perfecto. Ejercicio 4. Hallar los números primos \(p,q,r\) sabiendo que cumplen la ecuación \(p^2+pq+q^2=r^2\). Ejercicio 5. Encontrar las soluciones enteras de la ecuación \(x^3+y^3+z^3=63+3xyz\)
Una permutación es una manera de reordenar un conjunto. Hay un total de \(n!\) formas de reordenar un conjunto de \(n\) elementos distinguibles ya que hay \(n\) posibles elecciones para el primero de ellos, \(n-1\) para el segundo, y así sucesivamente.
El número de formas de elegir un subconjunto de \(k\) elementos de un conjunto de \(n\) elementos se llaman combinaciones de \(n\) elementos tomados de \(k\) en \(k\) y es igual al número combinatorio \[\binom{n}{k}=\frac{n(n-1)\cdots(n-k+1)}{k!}=\frac{n!}{k!(n-k)!}.\]
Un ejemplo particularmente útil es contar de cuántas maneras se pueden separar \(n\) elementos idénticos en \(k\) subconjuntos, para lo que sólo hay que ver cómo elegir \(k-1\) elementos, que actúan como separadores, de un conjunto de \(n+k-1\) elementos.
Ejercicio 1. Se consideran todos los números de 2024 dígitos que tienen todos sus dígitos iguales a 1, 2 o 3. ¿Cuántos de estos números hay? ¿En cuántos de ellos no hay dos dígitos consecutivos iguales? ¿En cuántos de ellos la diferencia entre dos dígitos cualesquiera consecutivos es exactamente 1? Ejercicio 2. ¿De cuántas formas se pueden dividir \(x+y+z\) objetos en tres grupos, de forma que en el primero haya \(x\) objetos, en el segundo \(y\) y en el tercero \(z\)? Ejercicio 3. ¿De cuántas formas se pueden distribuir 50 bolas blancas iguales en 10 cajas numeradas? ¿Y si hay 25 bolas rojas y 25 blancas? Ejercicio 4. ¿De cuántas formas se pueden pintar los vértices de un polígono regular de 100 lados de forma que haya exactamente 10 lados cuyos vértices tengan distinto color?Una ceviana de un triángulo \(ABC\) es un segmento que une un vértice con un punto de la recta que contiene al lado opuesto. Ejemplos muy conocidos de cevianas son las medianas, las bisectrices o las alturas de un triángulo (las mediatrices no, ya que no pasan por los vértices en general). En estos tres casos, las cevianas se cortan en un punto: el baricentro, el incentro y el ortocentro, respectivamente. El teorema de Ceva nos da una condición general para que tres cevianas, una saliendo de cada vértice de \(ABC\) se corten en un punto.
Dados \(X,Y,Z\) en las rectas \(BC,AC,AB\), respectivamente, distintos de los vértices. Las rectas cevianas \(AX,BY,CZ\) son concurrentes si, y sólo si, \[\left[\frac{CX}{BX}\right]\cdot\left[\frac{AY}{CY}\right]\cdot\left[\frac{BZ}{AZ}\right]=1.\] Los corchetes aquí indican la razón simple y hay que tener cuidado con su signo: por ejemplo, el cociente \([\frac{CX}{BX}]\) debe considerarse positivo si \(X\) está entre \(B\) y \(C\) y negativo si no lo está. Recordemos que \(X\) es cualquier punto de la recta \(BC\), no tiene por qué estar en el lado \(BC\) del triángulo. En la imagen se puede ver dos ejemplos de cevianas concurrentes en un punto \(P\), uno de ellos dentro del triángulo y otro fuera del triángulo.
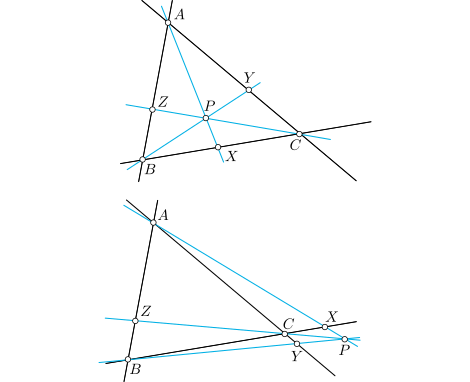 Ejercicio 1. Demostrar, usando el teorema de Ceva, que las medianas de un triángulo se cortan en un punto. Ejercicio 2. Demostrar, usando el teorema de Ceva, que las bisectrices de un triángulo se cortan en un punto (indicación: usar el teorema de la bisectriz). Ejercicio 3. Demostrar, usando el teorema de Ceva, que las alturas de un triángulo se cortan en un punto (observa que en este caso el punto de corte (ortocentro) puede ser exterior al triángulo). Ejercicio 4. Sea \(ABC\) un triángulo y supongamos que una circunferencia \(\Gamma\) corta a sus lados en los puntos \(X\) y \(R\) en \(BC\), \(Y\) e \(S\) en \(AC\) y \(Z\) y \(T\) en \(AB\). Si las cevianas \(AX\), \(BY\) y \(CZ\) son concurrentes, demuestra que \(AR\), \(BS\) y \(CT\) también son concurrentes.
Ejercicio 1. Demostrar, usando el teorema de Ceva, que las medianas de un triángulo se cortan en un punto. Ejercicio 2. Demostrar, usando el teorema de Ceva, que las bisectrices de un triángulo se cortan en un punto (indicación: usar el teorema de la bisectriz). Ejercicio 3. Demostrar, usando el teorema de Ceva, que las alturas de un triángulo se cortan en un punto (observa que en este caso el punto de corte (ortocentro) puede ser exterior al triángulo). Ejercicio 4. Sea \(ABC\) un triángulo y supongamos que una circunferencia \(\Gamma\) corta a sus lados en los puntos \(X\) y \(R\) en \(BC\), \(Y\) e \(S\) en \(AC\) y \(Z\) y \(T\) en \(AB\). Si las cevianas \(AX\), \(BY\) y \(CZ\) son concurrentes, demuestra que \(AR\), \(BS\) y \(CT\) también son concurrentes.Recordemos que dos números enteros \(a,b\in\mathbb{Z}\) son congruentes módulo otro entero \(m\in\mathbb{Z}\) cuando tienen el mismo resto al dividirlos entre \(m\) y esto se escribe como \(a\equiv b\ (\text{mod }m)\). Aunque todo entero es congruente con únicamente uno de los números \(1,2,\ldots,m-1\) (su resto), un cuadrado tiene muchas menos posibilidades. Por ejemplo, ¿serías capaz de comprobar las siguientes afirmaciones?
- Todo cuadrado es congruente con \(0\) o \(1\) módulo \(3\).
- Todo cuadrado es congruente con \(0\) o \(1\) módulo \(4\).
- Todo cuadrado es congruente con \(0\), \(1\) o \(4\) módulo \(5\).
- Todo cuadrado es congruente con \(0\), \(1\) o \(4\) módulo \(8\).
Tomemos dos conjuntos ordenados de \(n\) números:\begin{align*}&x_1\leq x_2\leq\ldots\leq x_n\\&y_1\leq y_2\leq\ldots\leq y_n \end{align*}Supongamos ahora que \(z_1,z_2,\ldots,z_n\) es una permutación de \(y_1,y_2,\ldots, y_n\), es decir, son los mismos números reordenados. Entonces, la suma \[x_1z_1+x_2x_2+\ldots+x_nz_n\]es máxima cuando \(z_i=y_i\) para todo \(i\) y es mínima cuando \(z_i=y_{n-i}\) para todo \(i\). En otras palabras, el máximo se obtienen cuando están ordenados en el mismo sentido y el mínimo cuando están ordenados en sentido contrario. Ejercicio 1. En un tablero \(3\times 3\) se colocan los números del 1 al 9 sin repetir ninguno. Sea \(S\) la suma de los tres números de tres cifras que se leen de derecha a izquierda y los tres que se leen de arriba abajo. ¿Cuál es el valor máximo y mínimo posible de \(S\)? Ejercicio 2. Sea \(x_1,\ldots,x_{100}\) una permutación de los números del 1 al 100. ¿Cuál es el valor máximo y mínimo posibles de la suma $$(x_1+1)^2+(x_2+2)^2+\ldots+(x_{100}+100)^2\text{?}$$¿Y si sustituimos los cuadrados por cubos? Ejercicio 3. Demostrar las siguientes desigualdades:
- \(xy+yz+xz\leq x^2+y^2+z^2\) para cualesquiera \(x,y,z\in\mathbb{R}\).
- \(x^2y+y^2z+z^2x\leq x^3+y^3+z^3\) para cualesquiera \(x,y,z\gt 0\).
- \(xyz^2+yzx^2+xzy^2\leq x^4+y^4+z^4\) para cualesquiera \(x,y,z\in\mathbb{R}\).
- \(x^4+y^4+z^4+w^4\geq 4xyzw\) para cualesquiera \(x,y,z,w\gt 0\).
- \(x^xy^yz^z\geq x^yy^zz^x\) para cualesquiera \(x,y,z\gt 0\).
- \(\frac{x^2}{y^2}+\frac{y^2}{z^2}+\frac{z^2}{x^2}\geq \frac{x}{z}+\frac{y}{x}+\frac{z}{y}\) para cualesquiera \(x,y,z\gt 0\).
Dados dos números reales \(x,y\in\mathbb{R}\), podemos desarrollar la potencia del binomio \(x+y\) de exponente natural \(n\in\mathbb{N}\) como $$(x+y)^n=\binom{n}{0}x^n+\binom{n}{1}x^{n-1}y+\binom{n}{2}x^{n-2}y^2+\ldots+\binom{n}{n}y^n.$$ Aquí entran en juego los números combinatorios $$\binom{n}{k}=\frac{n!}{k!(n-k)!}$$ que también pueden representarse en combinatoria como el número de subconjuntos de \(k\) elementos que pueden elegirse de un conjunto de \(n\) elementos y forman el conocido triángulo de Pascal. Ejercicio 1. Demuestra que si \(n,m,p\) son enteros y \(p\) es un número primo, entonces \((m+n)^p\equiv m^p+n^p\) módulo \(p\). Ejercicio 2. Demuestra la siguiente propiedad, que nos dice que en el triángulo de Pascal cada elemento es suma de los dos que están encima de él: $$\binom{n+1}{k+1}=\binom{n}{k}+\binom{n}{k+1}$$ Ejercicio 3. Demuestra las siguientes igualdades: $$\binom{n}{0}+\binom{n}{0}+\ldots\binom{n}{n}=2^n,$$ $$\binom{n}{0}^2+\binom{n}{1}^2+\ldots\binom{n}{n}^2=\binom{2n}{n}$$ Ejercicio 4. Hallar los enteros positivos \(n\) para los que \(\binom{n}{1},\binom{n}{2},\ldots,\binom{n}{n-1}\) son todos números pares. Ejercicio 5. Encuentra enteros positivos \(a, b\) tales que ninguno de los números \(a,b,a+b\) es divisible por \(7\) pero \((a + b)^7-a^7-b^7\) es divisible por \(7^2\).
Un lugar geométrico es el conjunto de puntos que cumplen una cierta propiedad o los posibles lugares que ocupa un punto cuando se modifica una construcción geométrica. Veamos algunos ejemplos muy bien conocidos:
- El lugar geométrico de los puntos que equidistan de dos puntos dados es la mediatriz del segmento que los une.
- El lugar geométrico de los puntos que equidistan de dos rectas secantes dadas son las bisectrices de los ángulos que forman.
- Una circunferencia es el lugar geométrico de los puntos que están a una distancia fija (radio) de un punto dado (centro).
- Una elipse es el lugar geométrico de los puntos cuya suma de distancias a dos puntos es constante.
- Una hipérbola es el lugar geométrico de los puntos cuya diferencias de distancias a dos puntos es constante.
Supongamos que tenemos una circunferencia y un punto \(P\) que no está sobre ella (\(P\) puede ser interior o exterior). Trazamos dos rectas que pasan por \(P\) y cortan a la circunferencia en los puntos \(A\) y \(B\) (una de ellas) y \(C\) y \(D\) (la otra). Entonces, se cumple que $$PA\cdot PB=PC\cdot PD,$$ es decir, el producto de las longitudes no depende de la recta. Esto también se cumple cuando una de las rectas es tangente, en cuyo caso tenemos que los dos puntos de corte son el mismo. Este producto se llama potencia del punto \(P\) respecto de la circunferencia y es igual a la distancia del \(P\) al centro al cuadrado menos el radio de la circunferencial al cuadrado (en valor absoluto ya que si \(P\) es interior a la circunferencia esta diferencia es negativa). Todo esto puede verse en la imagen.
 Ejercicio 1. Dos circunferencias secantes se cortan en los puntos \(A\) y \(B\) y tienen una recta tangente exterior común que las toca en \(P\) y \(Q\). Demuestra que la recta \(AB\) corta al segmento \(PQ\) en su punto medio. Ejercicio 2. En una circunferencia se dibujan dos cuerdas \(AB\) y \(CD\) que se cortan en un punto interior \(P\). Sabiendo que \(\frac{AP}{BP}=4\) y \(\frac{CP}{DP}=\frac{9}{4}\), ¿cuánto valen \(\frac{AB}{CD}\), \(\frac{AC}{BD}\) y \(\frac{AD}{BC}\)? Ejercicio 3. Sean \(A,B,C\) tres puntos de una circunferencia tales que \(AB=BC\). Las tangentes a esta circunferencia que pasan por \(A\) y \(B\) se cortan en un punto \(D\) y \(DC\) corta a la circunferencia de nuevo en otro punto \(E\). Demuestra que \(AE\) corta al segmento \(BD\) en su punto medio. Ejercicio 4. Demuestra la propiedad de la potencia buscando triángulos semejantes (la propiedad del arco capaz puede ser muy útil).
Ejercicio 1. Dos circunferencias secantes se cortan en los puntos \(A\) y \(B\) y tienen una recta tangente exterior común que las toca en \(P\) y \(Q\). Demuestra que la recta \(AB\) corta al segmento \(PQ\) en su punto medio. Ejercicio 2. En una circunferencia se dibujan dos cuerdas \(AB\) y \(CD\) que se cortan en un punto interior \(P\). Sabiendo que \(\frac{AP}{BP}=4\) y \(\frac{CP}{DP}=\frac{9}{4}\), ¿cuánto valen \(\frac{AB}{CD}\), \(\frac{AC}{BD}\) y \(\frac{AD}{BC}\)? Ejercicio 3. Sean \(A,B,C\) tres puntos de una circunferencia tales que \(AB=BC\). Las tangentes a esta circunferencia que pasan por \(A\) y \(B\) se cortan en un punto \(D\) y \(DC\) corta a la circunferencia de nuevo en otro punto \(E\). Demuestra que \(AE\) corta al segmento \(BD\) en su punto medio. Ejercicio 4. Demuestra la propiedad de la potencia buscando triángulos semejantes (la propiedad del arco capaz puede ser muy útil).Dos identidades muy interesantes son \begin{eqnarray*}x^n-y^n&=&(x-y)(x^{n-1}+x^{n-2}y+x^{n-3}y^2+\ldots+xy^{n-2}+y^{n-1}),\\x^n+y^n&=&(x+y)(x^{n-1}-x^{n-2}y+x^{n-3}y^2-\ldots-xy^{n-2}+y^{n-1}).\end{eqnarray*}La primera es cierta para todo exponente natural \(n\), mientras que la segunda sólo es cierta cuando \(n\) es impar. Estas identidades permiten factorizar expresiones con potencias y son muy útiles para resolver ecuaciones con números enteros o con números reales.
Una consecuencia de la primera de las dos identidades es que si \(P(x)\) es un polinomio con coeficientes enteros y \(a,b\) son números enteros, entonces \(P(a)-P(b)\) es divisible entre \(a-b\).
Ejercicio 1. Demuestra que si \(d\) es un divisor de \(n\), entonces \(x^n-y^n\) es divisible por \(x^d-y^d\). Ejercicio 2. Demuestra que no existe ningún polinomio \(P(x)\) con coeficientes enteros tal que \(P(1)=5\) y \(P(3)=6\). Ejercicio 3. Hallar los valores enteros de \(n\) para los que \(3^n-2^n\) es múltiplo de \(211\). Ejercicio 4. Sea \(P(x)\) un polinomio con coeficientes enteros tal que la ecuación \(P(x)=7\) tiene al menos cuatro soluciones enteras. Demostrar que la ecuación \(P(x)=14\) no tiene soluciones enteras.A la hora de contar cuántos elementos cumplen una de dos condiciones, podemos sumar los que cumplen cada una de ellas y luego restarle al resultado los que cumplen ambas. Esto se escribe matemáticamente como $$|A\cup B|=|A|+|B|-|A\cap B|,$$donde \(|X|\) indica el número de elementos de un conjunto \(X\), \(\cup\) es la unión y \(\cap\) es la intersección. En lo anterior, hemos escrito \(A\) como el conjunto de elementos que cumplen una de las dos condiciones y \(B\) el conjunto de los que cumplen la otra. De la misma forma, cuando tenemos tres condiciones (o conjuntos), podemos calcular \begin{eqnarray}|A\cup B\cup C|&=&|A|+|B|+|C|\\&&-|A\cap B|-|B\cap C|-|A\cap C|+|A\cap B\cap C|,\end{eqnarray}como se muestra en la imagen (fuente: Wikipedia).
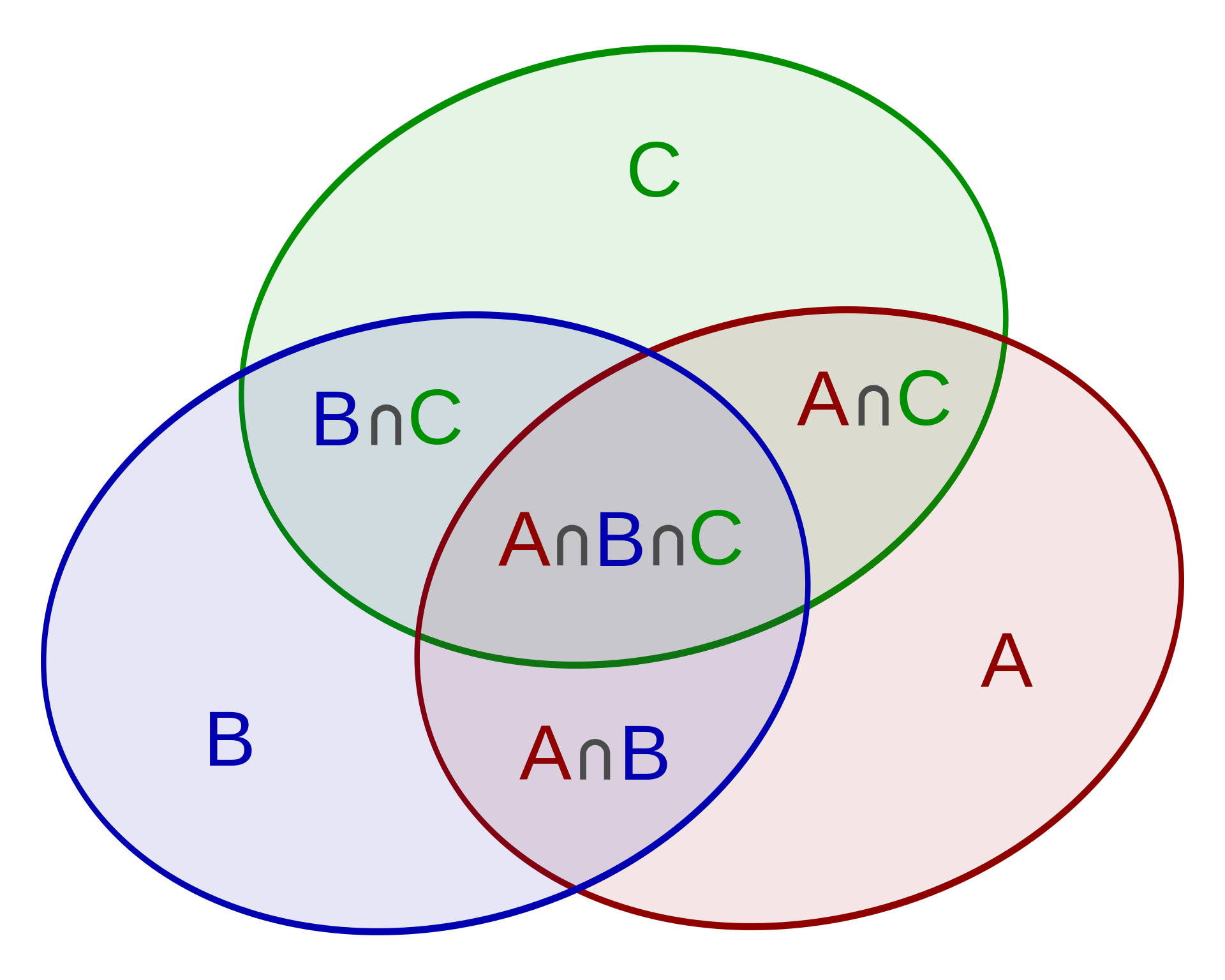 Ejercicio 1. ¿Cómo se escribe el principio de inclusión-exclusión para 4 conjuntos? ¿Y para 5? Ejercicio 2. ¿Cuántos números naturales entre 1 y 1000 tienen algún factor primo menor que 10? ¿Cuántos no son la potencia de ningún otro entero (mayor que 1)? Ejercicio 3. ¿De cuántas formas se pueden ordenar los números del 1 al 10 de forma que ninguno quede en su lugar? ¿De cuántas formas se pueden ordenar para que quede solo uno en su lugar? Ejercicio 4. ¿De cuántas formas se pueden ordenar los números enteros del 1 al \(n\) de forma que no haya dos números consecutivos uno al lado del otro?
Ejercicio 1. ¿Cómo se escribe el principio de inclusión-exclusión para 4 conjuntos? ¿Y para 5? Ejercicio 2. ¿Cuántos números naturales entre 1 y 1000 tienen algún factor primo menor que 10? ¿Cuántos no son la potencia de ningún otro entero (mayor que 1)? Ejercicio 3. ¿De cuántas formas se pueden ordenar los números del 1 al 10 de forma que ninguno quede en su lugar? ¿De cuántas formas se pueden ordenar para que quede solo uno en su lugar? Ejercicio 4. ¿De cuántas formas se pueden ordenar los números enteros del 1 al \(n\) de forma que no haya dos números consecutivos uno al lado del otro?Dados números reales positivos \((x_1,x_2,\ldots,x_n)\), se define \begin{align*}&\text{la media aritmética: }&M_a&=\frac{x_1+x_2+\ldots+x_n}{n},\\&\text{la media geométrica: }&M_g&=\sqrt[n]{x_1x_2\cdots x_n},\\&\text{la media cuadrática: }&M_q&=\sqrt{\frac{x_1^2+x_2^2+\ldots+x_n^2}{n}},\\&\text{la media armónica: }&M_h&=\frac{n}{\frac{1}{x_1}+\frac{1}{x_2}+\ldots+\frac{1}{x_n}}.\end{align*}Entonces, se cumple que \[M_h\leq M_g\leq M_a\leq M_q.\] Cada una de estas desigualdades se convierte en igualdad sólo cuando todos los números son iguales, es decir, cuando \(x_1=x_2=\ldots=x_n\). Ejercicio 1. Si \(a,b,c\) son números reales positivos, demuestra las siguientes desigualdades: \[a^2+b^2+c^2\geq ab+bc+ac,\]\[\frac{a}{b}+\frac{b}{c}+\frac{c}{a}\geq 1,\]\[a^3+b^3+c^3\geq a^2b+b^2c+c^2a,\]\[(a+b+c)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\geq 9,\]\[\frac{a^2}{b}+\frac{b^2}{c}+\frac{c^2}{b}\geq a+b+c,\]\[\frac{a^3}{bc}+\frac{b^3}{ac}+\frac{c^3}{ab}\geq a+b+c,\] Ejercicio 2. ¿Serías capaz de generalizar las desigualdades del Ejercicio 1 para \(n\) números reales positivos (en lugar de tres)? Ejercicio 3. Si \(x_1,x_2,\ldots,x_n\) son números reales positivos cuyo producto es \(1\), demuestra que \((1+x_1)(1+x_2)\ldots(1+x_n)\geq 2^n\). Ejercicio 4. Demuestra la desigualdad \(M_a\leq M_q\) a partir de la desigualdad de Cauchy-Schwarz y concluye que esta desigualdad sigue siendo cierta si algunos números son negativos.
Tomemos un polinomio \(p(x)\) de grado \(3\), es decir, \[p(x)=ax^3+bx^2+cx+d.\] El teorema fundamental del álgebra nos dice que puede factorizarse \[p(x)=a(x-\alpha)(x-\beta)(x-\gamma),\] donde \(\alpha,\beta,\gamma\) son las llamadas raíces del polinomio, que pueden ser números complejos. Si multiplicamos todos los paréntesis en esta factorización e igualamos los coeficientes de ambas expresiones para \(p(x)\), tenemos las llamadas relaciones de Cardano-Viète: \begin{align*}\alpha+\beta+\gamma&=-\frac{b}{a},\\\alpha\beta+\beta\gamma+\alpha\gamma&=\frac{c}{a},\\\alpha\beta\gamma&=-\frac{d}{a}.\end{align*} Tenemos así relaciones entre los coeficientes y las raíces del polinomio. En general, se puede hacer un razonamiento similar para polinomios de cualquier grado. Ejercicio 1. Escribe las ecuaciones de Cardano-Viète para polinomios de grados 2 y 4 Ejercicio 2. Si \(\alpha\) y \(\beta\) son las raíces del polinomio \(p(x)=x^2-3x+1\), halla los valores de \(\alpha\beta\), \(\alpha^2+\beta^2\), \(\alpha^3+\beta^3\) y \(\frac{1}{\alpha}+\frac{1}{\beta}\). Ejercicio 3. Sabemos que una de las raíces del polinomio \(p(x)=x^3+ax^2+bx+c\) es suma de las otras dos. Demostrar que \(a^3-4ab+8c=0\). Ejercicio 4. Si las raíces del polinomio \(p(x)=x^3+2cx^2-cx+10\) están en progresión aritmética, ¿cuáles son esas raíces?
Si más de \(nm\) palomas se colocan en \(n\) palomares, al menos uno de ellos tendrá más de \(m\) palomas. Ejercicio 1. Dados 100 números enteros, demuestra que podemos elegir 15 de ellos de forma que la diferencia entre dos cualesquiera de los elegidos es múltiplo de 7. Ejercicio 2. Demuestra que en una reunión siempre hay dos personas que le han dado la mano al mismo número de personas. Ejercicio 3. Si coloreamos cada diagonal de un hexágono regular de rojo o de azul, demostrar que hay tres vértices tales que los segmentos que los unen son del mismo color. Ejercicio 4. Si coloreamos cada punto del plano de rojo, azul o amarillo, demostrar que existe un rectángulo que tiene sus cuatro vértices del mismo color.
Un cuadrilátero \(ABCD\) se dice que es cíclico cuando existe una circunferencia que pasa por sus cuatro vértices (también se dice que \(ABCD\) está inscrito en tal circunferencia).
Por la propiedad del arco capaz, un \(ABCD\) es cíclico si, y sólo si, sus ángulos opuestos suman 180º. El teorema de Ptolomeo además nos dice que \(ABCD\) es cíclico si, y sólo si,\[AB\cdot CD+BC\cdot AD=AC\cdot BD.\] Ejercicio 1. Sea \(P\) un punto de la circunferencia circunscrita de un triángulo equilátero \(ABC\). Demuestra que la distancia de \(P\) a uno de los vértices es igual a la suma de distancias a los otros dos. Ejercicio 2. Demuestra que la diagonal de un pentágono regular de lado \(1\) mide \(\frac{1+\sqrt{5}}{2}\) (este número se conoce como la razón áurea) Ejercicio 3. En un triángulo \(ABC\), sean \(P\) y \(Q\) los pies de las alturas desde \(A\) y \(B\), respectivamente. Si la recta \(PQ\) es paralela a \(AB\), demuestra que el triángulo es isósceles. Ejercicio 4. Sea \(ABCD\) un cuadrilátero cíclico y pongamos que la perpendicular a \(AB\) que pasa por \(B\) corta a \(CD\) en un punto \(P\) y que la perpendicular a \(CD\) que pasa por \(D\) corta a \(AB\) en \(Q\). Demuestra que \(PQ\) es paralelo a \(AC\).
Ejercicio 1. Sea \(P\) un punto de la circunferencia circunscrita de un triángulo equilátero \(ABC\). Demuestra que la distancia de \(P\) a uno de los vértices es igual a la suma de distancias a los otros dos. Ejercicio 2. Demuestra que la diagonal de un pentágono regular de lado \(1\) mide \(\frac{1+\sqrt{5}}{2}\) (este número se conoce como la razón áurea) Ejercicio 3. En un triángulo \(ABC\), sean \(P\) y \(Q\) los pies de las alturas desde \(A\) y \(B\), respectivamente. Si la recta \(PQ\) es paralela a \(AB\), demuestra que el triángulo es isósceles. Ejercicio 4. Sea \(ABCD\) un cuadrilátero cíclico y pongamos que la perpendicular a \(AB\) que pasa por \(B\) corta a \(CD\) en un punto \(P\) y que la perpendicular a \(CD\) que pasa por \(D\) corta a \(AB\) en \(Q\). Demuestra que \(PQ\) es paralelo a \(AC\).
Dos números enteros son congruentes módulo \(m\) si dan el mismo resto al dividirlos entre \(m\) y lo escribimos como \(a\equiv b\,(\text{mod }m)\). Las congruencias se pueden sumar y multiplicar. Por ejemplo, si \(a\equiv 3\,(\text{mod }7)\) y \(a\equiv 4\,(\text{mod }7)\), entonces \(a+b\equiv 3+4=7\equiv 0\,(\text{mod }7)\) y, por tanto, \(a+b\) es múltiplo de \(7\). Por otro lado, \(ab\equiv 3\cdot 4=12\equiv 5\,(\text{mod }7)\).
Las potencias \(a^n\) repiten periódicamente su resto módulo \(m\) cuando variamos el exponente \(n\). Esto se puede usar para calcular rápidamente restos de potencias si hallamos un exponente \(q\) tal que \(a^q\equiv 1\,(\text{mod }m)\), pues en tal caso \(a^{kq+r}\equiv a^r\,(\text{mod }m)\).
El teorema pequeño de Fermat nos dice que \(a^{p-1}\equiv 1\,(\text{mod }p)\) si \(p\) es un número primo y \(a\) es un entero que no es divisible entre \(p\).
Ejercicio 1. Demuestra que \(2222^{5555}+5555^{2222}\) es múltiplo de \(7\). Ejercicio 2. Halla las dos últimas cifras de \(3^{1000000}\). Ejercicio 3. Si \(p\gt 5\) es un número primo, demuestra que \(\frac{1}{p}\) es un número decimal periódico puro con periodo formado por \(p-1\) dígitos.Si \(x_1,x_2,\ldots,x_n,y_1,y_2,\ldots,y_n\) son números reales cualesquiera, entonces \[(x_1y_1+x_2y_2+\ldots+x_ny_n)^2\leq(x_1^2+\ldots+x_n^2)(y_1^2+\ldots+y_n^2).\] Esta desigualdad se convierte en igualdad solo si existen \(a,b\in\mathbb{R}\) tales que \(ax_i+by_i=0\) para todo subíndice \(i\in\{1,\ldots,n\}\). Ejercicio 1. Demuestra que, si \(n\) es un número natural, entonces \[1^2+2^2+\ldots+n^2\leq(1+2+\ldots+n)(1^3+2^3+\ldots+n^3).\] Ejercicio 2. Demuestra que para cualesquiera números reales \(x_1,\ldots,x_n\) se cumple que \[(x_1+x_2+\ldots+x_n)^2\leq n(x_1^2+x_2^2+\ldots+x_n^2).\] Ejercicio 3. Si \(a,b,c\) son números reales positivos tales que \(a+b+c=1\), ¿Cuál es el valor máximo posible de \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\)?

