Olimpiadas de Matemáticas
Página de preparación y problemas

Solución. Observemos que en la figura se forman tres pentagonos y dos cuadrados. Evidentemente, nuestra curva tendría que empezar fuera de (al menos) dos de los pentágonos. Cada vez que la curva atraviesa un lado de uno de estos pentágonos pasará de estar en el interior a estar en el exterior o del exterior al interior. Por tanto, como cada pentágono tiene un número impar de lados, la curva debería terminar en el interior de dos de los pentágonos, lo cual es absurdo. Concluimos que no existe dicha curva.

Solución. Esta es una solución muy estándar usando algo de teoría de grafos. La figura del enunciado es un grafo plano y podemos considerar el grafo dual, que tiene un vértice por cada cara del grafo original y en el que dos vértices se unen por una arista cuando representan a caras adyacentes (ver figura).

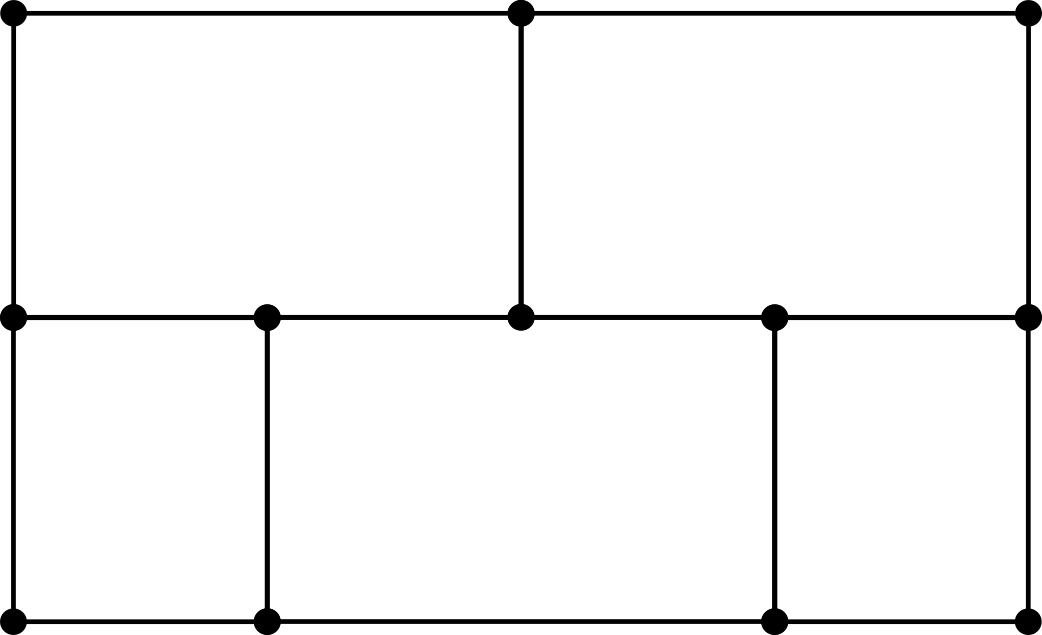
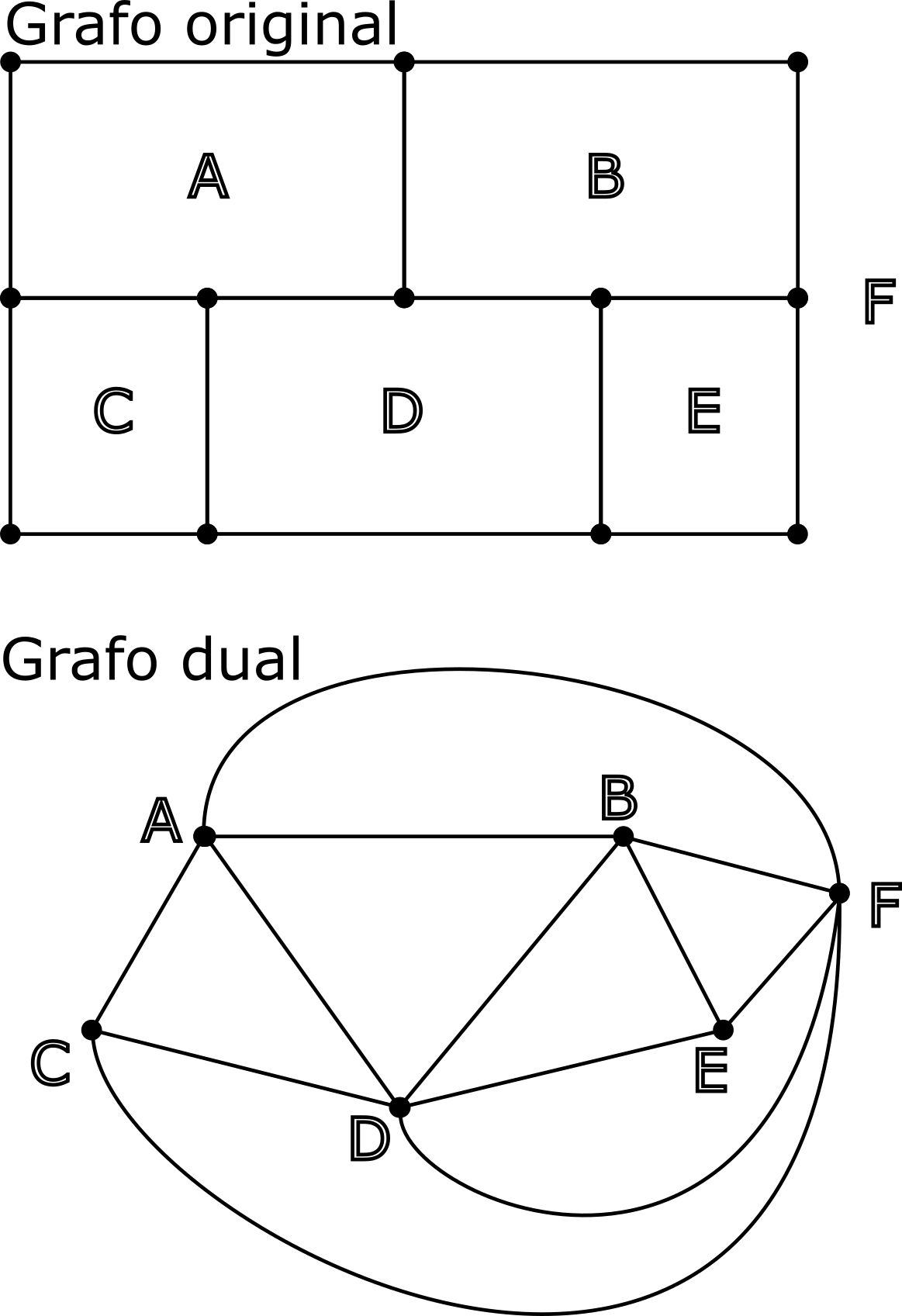
Atravesar una arista del grafo original equivale a recorrer una arista del grafo dual, por lo que el problema se reduce a encontrar un camino que pase por todas las aristas del grafo dual una sola vez. Esto no puede hacerse ya que eso implicaría que hay como máximo dos vértices del grafo dual a los que llegan un número par de aristas (Teorema de Euler). Sin embargo, el grafo dual tiene 4 vértices (C, D, E y F) a los que llegan un número par de aristas, por lo que concluimos que la curva buscada no puede existir.

Solución. Sean $r$ y $s$ las tangentes exteriores a las circunferencias de centros $A$ y $C$ y $r'$ y $s'$ las tangentes exteriores a las circunferencias de centros $B$ y $D$. Una circunferencia tangente a $r$ y $s$ debe equidistar de ambas rectas por lo que su centro pertenece a la bisectriz del ángulo formado por estas (si $r$ y $s$ son paralelas, entonces el centro pertenece a una paralela equidistante a ambas). Esto nos dice que las circunferencias tangentes a $r$ y $s$ tienen su centro en una recta, luego esta debe ser la que contiene a la diagonal $AC$. De la misma forma, debe pertenecer a la diagonal $BD$, luego el centro ha de ser el centro del rectángulo, que denotaremos por $O$.

Consideremos $A'$, $O'$ y $C'$ los pies de las perpendiculares a $r$ que pasan por $A$, $O$ y $C$. Como $AO=OC$, se deduce del teorema de Tales (las rectas $r$ y $AC$ son cortadas por tres paralelas $AA'$, $OO'$ y $CC'$) que $OO'=\frac{1}{2}(AA'+CC')=\frac{1}{2}(a+c)$. Por tanto, la circunferencia con centro $O$ y tangente a $r$ y $s$ tiene radio $\frac{1}{2}(a+c)$. Análogamente, la circunferencia con centro $O$ y tangente a $r'$ y $s'$ tiene radio $\frac{1}{2}(b+d)$. Como $a+c=b+d$, deducimos que ambas son la misma circunferencia y, por tanto, el cuadrilátero que se forma admite una circunferencia inscrita.

Solución. Entre los $39$ números siempre hay $20$ consecutivos $n,n+1,\ldots,n+19$ que sólo difieren en las cifras de las decenas y las unidades y de forma que la cifra de la cifra de las unidades de $n$ es cero. Si $a$ es la suma de las cifras de $n$, entonces las sumas de las cifras de $n,n+1,\ldots,n+19$ son $a,a+1,\ldots,a+9,a+1,\ldots,a+10$, respectivamente, y alguno de estos números ha de ser múltiplo de $11$.

Nota. Un ejemplo de que el resultado no es cierto para $38$ números son los números del $999981$ al $1000018$.

Solución. Hay muchas disposiciones de fichas para responder a la primera pregunta. Después de hacer algunas pruebas, llegaremos a alguna de ellas. Por ejemplo, una solución es

$\bigcirc$	$\bigcirc$
	$\bigcirc$	$\bigcirc$
$\bigcirc$		$\bigcirc$
			$\bigcirc$

ya que al eliminar dos filas cualesquiera, las fichas restantes ocupan tres columnas.

Para responder a la última pregunta, supongamos que tenemos sólo 6 fichas. Tiene que haber dos filas que contengan 4 fichas entre ambas (si no fuera así, habría máximo una fila con dos fichas y tres filas con una ficha, lo cual da un total de sólo 5 fichas). Por tanto, tomando estas dos filas y las columnas donde estén las 2 fichas restantes, hemos terminado.

Solución. Supongamos que $a,b,c,d>0$ cumplen que, después de repetir el proceso un número determinado de veces, se vuelven a obtener dichos números. Observemos que $a_1b_1c_1d_1=(abcd)^2$, luego en cada paso del proceso el producto de los cuatro números se eleva al cuadrado. Como llegado un momento han de repetirse los números, esto implica que $abcd=1$. Ahora es fácil obtener más iteraciones: \[\begin{array}{llll} a_2=ab^2c,&b_2=bc^2d,&c_2=cd^2a,&d_2=da^2b\\ a_3=b^2c^2,&b_3=c^2d^2,&c_3=d^2c^2,&c_4=a^2b^2 \end{array}\] y, en general, no es difícil comprobar que $a_{2n+1},b_{2n+1},c_{2n+1},d_{2n+1}$ son los números $a^{2n}b^{2n}$, $b^{2n}c^{2n}$, $c^{2n}d^{2n}$ y $d^{2n}a^{2n}$ (aunque posiblemente en otro orden). Por tanto, en la sucesión de iteraciones aparecen los números $(a^2b^2)^n$, $(b^2c^2)^n$, $(c^2d^2)^n$ y $(d^2a^2)^n$. Si queremos que los números originales vuelvan a repetirse, se habrá de cumplir que $a^2b^2=b^2c^2=c^2d^2=a^2d^2=1$ pues en caso contrario habría infinitos términos distintos. De aquí deducimos que $ab=bc=cd=da=1$ y, de esta condición, es fácil llegar a que $a=c=x$ y $b=d=\frac{1}{x}$ para cierto $x>0$. Esto nos dice que a partir de la segunda iteración todos los términos son iguales a $1$ luego tiene que ser $x=1$ y hemos terminado.

Para probar el apartado (b), es fácil ver que el primer término de la sucesión evoluciona de la siguiente manera: \[a_1\mapsto a_1a_2\mapsto a_1a_2^2a_3\mapsto a_1a_2^3a_3^3a_4\mapsto a_1a_2^4a_3^6a_4^4a_5\mapsto\ldots\] de forma que los exponentes son números combinatorios. Después de $n-1$ iteraciones, obtenemos que el primer término se convierte en \[a_1a_2^{\binom{n-1}{1}}a_3^{\binom{n-1}{2}}\ldots a_{n-1}^{\binom{n-1}{n-1}}a_n.\] Análogamente, tras $n-1$ iteraciones, el segundo término se convierte en \[a_2a_3^{\binom{n-1}{1}}a_4^{\binom{n-1}{2}}\ldots a_n^{\binom{n-1}{n-1}}a_1\] ya que los índices van rotando cíclicamente. En consecuencia, tras $n$ iteraciones el primer término se convierte en \[a_1^2a_2^{\binom{n}{1}}a_3^{\binom{n}{2}}\ldots a_{n-1}^{\binom{n}{n-1}}a_n^2.\] El primer y último exponentes son pares. Veamos que $\binom{n}{k}$ es también par para $k$ entre $1$ y $n$. Ahora bien, podemos expresar \[\binom{n}{k}=\frac{n!}{k!(n-k)!}=\frac{n}{n-k}\frac{(n-1)!}{k!(n-k-1)!}=\frac{n}{n-k}\binom{n-1}{k-1}.\] Como $\binom{n-1}{k-1}$ es un número entero y el exponente de $2$ en la factorización de $n-k$ es menor que en la de $n$ (ya que $n$ es potencia de $2$), concluimos que $\binom{n}{k}$ es par y, en consecuencia, que $a_1$ se convierte en positivo tras $n$ iteraciones. Se razona de forma análoga para probar que el resto de números son positivos tras $n$ iteraciones.

Solución. Usando números complejos, expresaremos los centros $O_a$ y $O_b$ como $a_0,b_0\in\mathbb{C}$, de donde las trayectorias $a(t)$ y $b(t)$ de los puntos $A$ y $B$ en función del tiempo $t$ se escriben como \[a(t)=a_0+re^{it},\qquad b(t)=b_0+se^{it},\] donde $r,s\in\mathbb{C}$ son números complejos no nulos cuyos módulos son los radios de las circunferencias. Cambiando $A$ por $B$ si fuera necesario, podemos suponer que el punto $C$ se obtiene rotando el punto $B$ un ángulo $\frac{\pi}{3}$ en el sentido antihorario con centro en $A$, lo que nos da la trayectoria \begin{align*} c(t)&=a(t)+e^{i\pi/3}(b(t)-a(t))=a_0+re^{it}+e^{i\pi/3}(b_0-a_0+(r-s)e^{it})\\ &=[a_0+e^{i\pi/3}(b_0-a_0)]+[r+e^{i\pi/3}(r-s)]e^{it}. \end{align*} Esta vuelve a ser la trayectoria de una circunferencia y además muestra que su centro $a_0+e^{i\pi/3}(b_0-a_0)$ forma un triángulo equilátero con los centros $O_a$ y $O_b$. Notemos que $c(t)$ podría ser constante si la circunferencia tiene radio cero, es decir si $r+e^{i\pi/3}(r-s)=0$.

El apartado (b) es consecuencia de la desigualdad de Ptolomeo aplicada a los cuatro puntos $A,C,B,P$, que nos dice que \[CP\cdot AB\leq AP\cdot BC+BP\cdot AC\ \Longleftrightarrow\ CP\leq AP+BP=2+3=5,\] ya que $AB=BC=CA$. Además, sabemos que si $ACBP$ es un cuadrilátero cíclico, entonces la igualdad se alcanza. Por tanto, el máximo anterior $CP=5$ se alcanza cuando $P$ está en el arco menor $AB$ de la circunferencia circunscrita del triángulo $ABC$. En este caso, el triángulo $ABP$ tiene lados $AP=2$ y $BP=3$ que forman un ángulo de $120^\circ$ por la propiedad del arco capaz, de forma que el teorema del coseno nos da necesariamente \[AB^2=2^2+3^2-2\cdot 2\cdot 3\cos(120^\circ)=19.\] Deducimos así que el máximo $CP=5$ se alcanza efectivamente para un triángulo de lado $\sqrt{19}$ cuando el punto $P$ está en el arco menor $AB$.

Solución. Sea $S$ la suma total de los elementos de la tabla. Cada vez que nos encontremos una fila o columna con suma negativa la cambiamos de signo. Cada una de estas operaciones incrementa el valor de $S$ y, como hay un número limitado de combinaciones de signos (es menor o igual que $2^{mn}$, el número de elecciones de signos $\pm$ en los $mn$ elementos de la tabla), este proceso no puede continuar indefinidamente, es decir, llegamos a un punto en el que todas las filas y columnas tienen suma positiva.

Solución. Procedamos por inducción sobre $n$. El caso base es $n=2$, en cuyo caso hay necesariamente dos puntos unidos por $n-1=1$ segmentos y no hay nada que probar. Supongamos entonces que el enunciado es cierto tal cual está escrito para $n$ puntos y veamos lo que pasa si tenemos $n+1$ puntos con dicha propiedad. Al hacer un camino a lo largo de los segmentos sin repetir segmento, como no podemos volver a ningún punto ya visitado (habría dos caminos distintos con el mismo origen y el mismo final), llegará un momento en que no podremos seguir y habremos alcanzado un punto $p_0$ al que solo llega un segmento (mediante el cual hemos accedido a $p_0$). Si eliminamos $p_0$ y dicho segmento, tendremos $n$ puntos que verifican la misma propiedad, luego la hipótesis de inducción nos asegura que el número de segmentos es $n-1$. Añadiendo el que hemos eliminado, deducimos que el número de segmentos para $n+1$ puntos es $n$, como queríamos probar.

Solución. Para fijar la notación, supondremos que $A$ hace dos montones $x$ e $y$ fichas, donde $x+y=N$ y supondremos que $2\leq x\leq y$. Entonces, $b$ divide $x=x_1+x_2$ e $y=y_1+y_2$ con $1\leq x_1\leq x_2$ y $1\leq y_1\leq y_2$. Hay cuatro posibles ordenaciones para los montones cumpliendo estas restricciones: \begin{align*} (1)&\quad x_1\leq x_2\leq y_1\leq y_2,& (2)&\quad x_1\leq y_1\leq x_2\leq y_2,\\ (3)&\quad y_1\leq x_1\leq x_2\leq y_2,& (4)&\quad x_1\leq y_1\leq y_2\leq x_2. \end{align*} La jugada óptima es que $B$ hará las divisiones para obtener el máximo número posible de fichas mientras que $A$ hará las divisiones para que este máximo sea el mínimo posible.

Caso $R_1$. En los escenarios (1) y (2), $B$ obtiene $x_1+y_2\leq y$ fichas, en el (3) obtiene $y_1+y_2=y$ y en el (4) $x_1+x_2=x\leq y$, luego siempre obtiene a lo sumo $y$ fichas y puede forzar que así sea dividiendo el montón de $y$ en $y_1=1$ e $y_2=y-1$. Esto lo sabe $A$, que intentará minimizar $y$, el montón más grande, y en consecuencia elegirá $x=\lfloor\frac{N}{2}\rfloor$ e $y=\lfloor\frac{N+1}{2}\rfloor$ para jugar de forma óptima, lo que nos dice que $B$ se quedará con $y=\lfloor\frac{N+1}{2}\rfloor$ y $A$ con las $\rfloor\frac{N}{2}\lfloor$ restantes (ver la nota).

Caso $R_2$. En los escenarios (1) y (2), $B$ obtiene $x_2+y_1\geq x$ fichas, en el (3) obtiene $x_1+x_2=x$ y en el (4) obtiene $y_1+y_2=y\geq x$, luego siempre obtiene al menos $x$ fichas. En este caso, $A$ puede forzar a que se tenga el escenario (1) tomando $x=2$ e $y=N-2$, dejando a $B$ necesariamente con $x_1=x_2=1$ y entonces la mejor opción para $B$ es tomar $y_1=\lfloor\frac{N-2}{2}\rfloor$ e $y_2=\lfloor\frac{N-1}{2}\rfloor$ (maximizando $y_1$), de forma que $B$ se lleva $x_2+y_1=1+\lfloor\frac{N-2}{2}\rfloor=\lfloor\frac{N}{2}\rfloor$ y $A$ las restantes. Esta es la mejor estrategia para $A$, ya que si no hiciera $x=2$, entonces $B$ podría tomar $x_1=1$, $x_2=x-1$, $y_1=\lfloor\frac{N-x}{2}\rfloor$ e $y_2=\lfloor\frac{N-x+1}{2}\rfloor$. Distingamos dos subcasos:

• Si de este modo $B$ llega a los escenarios (1), (2) o (3), entonces obtendría al menos $x_2+y_1=x-1+\lfloor\frac{N-x}{2}\rfloor=\lfloor\frac{N+x-2}{2}\rfloor\geq \lfloor\frac{N+1}{2}\rfloor$ fichas, contradiciendo que $A$ ha tomado la estrategia óptima.
• Si, por el contrario, se llega al escenario (4), entonces $B$ obtiene $y_1+y_2=\lfloor\frac{N+1}{2}\rfloor$ y $A$ tampoco habría jugado óptimamente.

Caso $R_3$. La mejor estrategia a priori para $B$ es tomar $R_1$, luego tenemos que $A$ debe dividir necesariamente en partes $x=\lfloor\frac{N}{2}\rfloor$ e $y=\lfloor\frac{N+1}{2}\rfloor$, para minimizar las pérdidas y jugar de forma óptima. Sin embargo queda por ver que ante tal elección de $A$, $B$ no puede aprovechar la ocasión y elegir $R_2$ para mejorar sus ganancias. Sin embargo, como $x$ e $y$ se diferencian a lo sumo en una unidad, el montón mayor y el menor tienen que venir ambos de $x$ o ambos de $y$ (podría haber empates), luego eligiendo $R_1$ o $R_2$ se llevaría un máximo de $y=\lfloor\frac{N+1}{2}\rfloor$ fichas y hemos probado así que no puede aprovecharse del cambio de estrategia.

Nota. Hemos usado repetidamente que dividir un montón de $n$ fichas en dos partes lo más parecidas posibles es hacer los montones de $\lfloor \frac{n}{2}\rfloor$ y $\lfloor\frac{n+1}{2}\rfloor$ fichas. Esto evita distinguir si el número es par o impar, lo cual sería muy tedioso de escribir.

Solución. Consideremos la primera sucesión; si no está acotada, entonces admite una subsucesión estrictamente creciente; si está acotada, entonces toma solo un número finito de valores y existe una subsucesión que sea constante. En cualquiera de los dos casos, tenemos una subsucesión creciente de la primera sucesión. Consideramos la subsucesión de la segunda sucesión formada por los mismos índices, a la que puede aplicarse el mismo razonamiento para pasar a una subsucesión creciente. Finalmente, consideramos los términos de la tercera sucesión con los mismos índices que en la segunda subsucesión y aplicamos el mismo razonamiento. Para los (infinitos) índices de la tercera subsucesión, las tres sucesiones nos dan subsucesiones creciente luego pueden elegirse $m$ y $n$ cualesquiera índices de entre ellos y tenemos la propiedad buscada.

Nota. El resultado puede extenderse a cualquier número finito de sucesiones.

Solución. Cada cuadrado excluye un área mayor que la suya para el posible centro del círculo que queremos colocar. Como dicho centro ha de estar a distancia mayor que $\frac{1}{2}$ del cuadrado, esto implica que cada cuadrado excluye un área de $3+\frac{\pi}{4}$: el propio cuadrado, dos rectángulos de dimensiones $\frac{1}{2}\times 1$ pegados a cada lado y cuatro cuartos de círculo de radio $\frac{1}{2}$ pegados a sus esquinas. Esto excluye como máximo un área de $120(3+\frac\pi4)$. Además, como el círculo ha de estar dentro del rectángulo, el centro no podrá estar a distancia menor que $\frac{1}{2}$ del borde del rectángulo. En consecuencia, queda mínimo un área de $19\cdot 24-120(3+\frac\pi4)=96-30\pi$. Este número es positivo ya que $\frac{96}{30}=3.2\gt\pi$, luego siempre habrá puntos donde centrar el círculo cumpliendo las condiciones propuestas.

Solución. Sea $S$ la suma total de los elementos de la tabla. Cada vez que nos encontremos una fila o columna con suma negativa la cambiamos de signo. Cada una de estas operaciones incrementa el valor de $S$ y, como hay un número limitado de combinaciones de signos (es menor o igual que $2^{mn}$, el número de elecciones de signos $\pm$ en los $mn$ elementos de la tabla), este proceso no puede continuar indefinidamente, es decir, llegamos a un punto en el que todas las filas y columnas tienen suma positiva.

Solución. Usando números complejos, expresaremos los centros $O_a$ y $O_b$ como $a_0,b_0\in\mathbb{C}$, de donde las trayectorias $a(t)$ y $b(t)$ de los puntos $A$ y $B$ en función del tiempo $t$ se escriben como \[a(t)=a_0+re^{it},\qquad b(t)=b_0+se^{it},\] donde $r,s\in\mathbb{C}$ son números complejos no nulos cuyos módulos son los radios de las circunferencias. Cambiando $A$ por $B$ si fuera necesario, podemos suponer que el punto $C$ se obtiene rotando el punto $B$ un ángulo $\frac{\pi}{3}$ en el sentido antihorario con centro en $A$, lo que nos da la trayectoria \begin{align*} c(t)&=a(t)+e^{i\pi/3}(b(t)-a(t))=a_0+re^{it}+e^{i\pi/3}(b_0-a_0+(r-s)e^{it})\\ &=[a_0+e^{i\pi/3}(b_0-a_0)]+[r+e^{i\pi/3}(r-s)]e^{it}. \end{align*} Esta vuelve a ser la trayectoria de una circunferencia y además muestra que su centro $a_0+e^{i\pi/3}(b_0-a_0)$ forma un triángulo equilátero con los centros $O_a$ y $O_b$. Notemos que $c(t)$ podría ser constante si la circunferencia tiene radio cero, es decir si $r+e^{i\pi/3}(r-s)=0$.

El apartado (b) es consecuencia de la desigualdad de Ptolomeo aplicada a los cuatro puntos $A,C,B,P$, que nos dice que \[CP\cdot AB\leq AP\cdot BC+BP\cdot AC\ \Longleftrightarrow\ CP\leq AP+BP=2+3=5,\] ya que $AB=BC=CA$. Además, sabemos que si $ACBP$ es un cuadrilátero cíclico, entonces la igualdad se alcanza. Por tanto, el máximo anterior $CP=5$ se alcanza cuando $P$ está en el arco menor $AB$ de la circunferencia circunscrita del triángulo $ABC$. En este caso, el triángulo $ABP$ tiene lados $AP=2$ y $BP=3$ que forman un ángulo de $120^\circ$ por la propiedad del arco capaz, de forma que el teorema del coseno nos da necesariamente \[AB^2=2^2+3^2-2\cdot 2\cdot 3\cos(120^\circ)=19.\] Deducimos así que el máximo $CP=5$ se alcanza efectivamente para un triángulo de lado $\sqrt{19}$ cuando el punto $P$ está en el arco menor $AB$.

Solución. Supongamos que $a,b,c,d>0$ cumplen que, después de repetir el proceso un número determinado de veces, se vuelven a obtener dichos números. Observemos que $a_1b_1c_1d_1=(abcd)^2$, luego en cada paso del proceso el producto de los cuatro números se eleva al cuadrado. Como llegado un momento han de repetirse los números, esto implica que $abcd=1$. Ahora es fácil obtener más iteraciones: \[\begin{array}{llll} a_2=ab^2c,&b_2=bc^2d,&c_2=cd^2a,&d_2=da^2b\\ a_3=b^2c^2,&b_3=c^2d^2,&c_3=d^2c^2,&c_4=a^2b^2 \end{array}\] y, en general, no es difícil comprobar que $a_{2n+1},b_{2n+1},c_{2n+1},d_{2n+1}$ son los números $a^{2n}b^{2n}$, $b^{2n}c^{2n}$, $c^{2n}d^{2n}$ y $d^{2n}a^{2n}$ (aunque posiblemente en otro orden). Por tanto, en la sucesión de iteraciones aparecen los números $(a^2b^2)^n$, $(b^2c^2)^n$, $(c^2d^2)^n$ y $(d^2a^2)^n$. Si queremos que los números originales vuelvan a repetirse, se habrá de cumplir que $a^2b^2=b^2c^2=c^2d^2=a^2d^2=1$ pues en caso contrario habría infinitos términos distintos. De aquí deducimos que $ab=bc=cd=da=1$ y, de esta condición, es fácil llegar a que $a=c=x$ y $b=d=\frac{1}{x}$ para cierto $x>0$. Esto nos dice que a partir de la segunda iteración todos los términos son iguales a $1$ luego tiene que ser $x=1$ y hemos terminado.

Para probar el apartado (b), es fácil ver que el primer término de la sucesión evoluciona de la siguiente manera: \[a_1\mapsto a_1a_2\mapsto a_1a_2^2a_3\mapsto a_1a_2^3a_3^3a_4\mapsto a_1a_2^4a_3^6a_4^4a_5\mapsto\ldots\] de forma que los exponentes son números combinatorios. Después de $n-1$ iteraciones, obtenemos que el primer término se convierte en \[a_1a_2^{\binom{n-1}{1}}a_3^{\binom{n-1}{2}}\ldots a_{n-1}^{\binom{n-1}{n-1}}a_n.\] Análogamente, tras $n-1$ iteraciones, el segundo término se convierte en \[a_2a_3^{\binom{n-1}{1}}a_4^{\binom{n-1}{2}}\ldots a_n^{\binom{n-1}{n-1}}a_1\] ya que los índices van rotando cíclicamente. En consecuencia, tras $n$ iteraciones el primer término se convierte en \[a_1^2a_2^{\binom{n}{1}}a_3^{\binom{n}{2}}\ldots a_{n-1}^{\binom{n}{n-1}}a_n^2.\] El primer y último exponentes son pares. Veamos que $\binom{n}{k}$ es también par para $k$ entre $1$ y $n$. Ahora bien, podemos expresar \[\binom{n}{k}=\frac{n!}{k!(n-k)!}=\frac{n}{n-k}\frac{(n-1)!}{k!(n-k-1)!}=\frac{n}{n-k}\binom{n-1}{k-1}.\] Como $\binom{n-1}{k-1}$ es un número entero y el exponente de $2$ en la factorización de $n-k$ es menor que en la de $n$ (ya que $n$ es potencia de $2$), concluimos que $\binom{n}{k}$ es par y, en consecuencia, que $a_1$ se convierte en positivo tras $n$ iteraciones. Se razona de forma análoga para probar que el resto de números son positivos tras $n$ iteraciones.