Olimpiadas de Matemáticas
Página de preparación y problemas

Solución. Llamemos $\Gamma_1,\Gamma_2,\Gamma_3,\Gamma_4,\Gamma_5$ a las circunferencias y supongamos por hipótesis que existen puntos $p_1,p_2,p_3,p_4,p_5$ tales que $p_i\in\Gamma_j$ siempre que $j\neq i$. Si dos de estos puntos son iguales, entonces hemos terminado (por ejemplo, si $p_1=p_2$, entonces este punto está en las cinco circunferencias puesto que $p_1$ está en todas menos en $\Gamma_1$, pero $p_2$ sí que está en $\Gamma_1$).

Supongamos entonces que los cinco puntos $p_1,p_2,p_3,p_4,p_5$ son distintos. En particular, $p_1,p_2,p_3$ son tres puntos distintos tanto en $\Gamma_4$ como en $\Gamma_5$. Como tres puntos distintos determinan una única circunferencia, deducimos que $\Gamma_4=\Gamma_5$, luego $p_5$ está también en $\Gamma_5$ y, por tanto, es un punto común a todas las circunferencias.

Solución. Cada equipo juega un total de 7 partidos luego se lleva como máximo 14 puntos. Por un lado, no puede haber dos equipos con 13 y 14 puntos, puesto que entonces querría decir que el de 14 le ha ganado a todos (en particular, al que ha sacado 13), pero el que tiene 13 ha ganado a todos salvo a uno con el que ha empatado. Esto nos dice que el segundo clasificado tiene como máximo 12 puntos. Por otro lado, si nos fijamos en los cuatro equipos con menos puntos, han jugado entre sí un total de 6 partidos en los que se han repartido 12 puntos, luego estos cuatro equipos tienen una suma de al menos 12 puntos. Con la condición del enunciado deducimos que el segundo clasificado tiene 12 puntos y que los cuatro equipos con menos puntos han perdido todos sus partidos contra los cuatro equipos con más puntos. Por lo tanto, el equipo que quedó en tercer lugar ganó contra el equipo que quedó en séptimo lugar.

Solución. Para el apartado (a), sea $ABCD$ un cuadrilátero convexo y $P$ el punto de corte de sus diagonales. Si llamamos $X$ e $Y$ las proyecciones de $A$ y $C$ sobre la diagonal $BD$, debe cumplirse que $AX=CY$ para que los triángulos $ABD$ y $BCD$ tienen la misma área (observemos que $BD$ actúa como base común de ambos triángulos). Como $AXP$ y $CYP$ son semejantes por estar en posición de Thales, se sigue que son congruentes y $AP=CP$. De la misma forma se prueba que $BP=DP$, luego las diagonales de $ABCD$ se cortan en su punto medio y el cuadrilátero tiene que ser un paralelogramo.

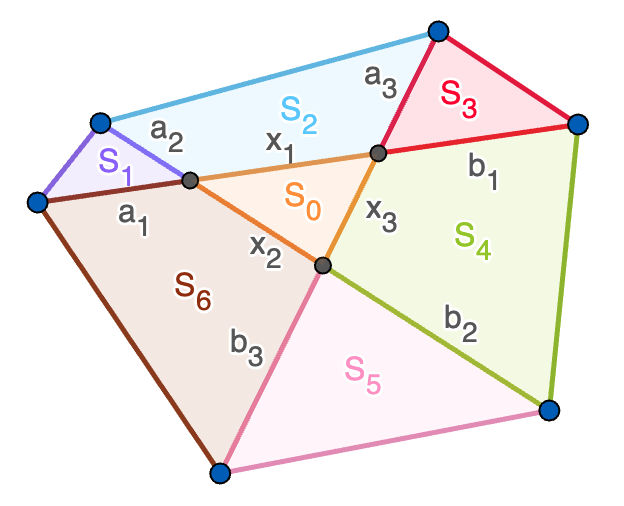
En cuanto al apartado (b), supongamos que tenemos un hexágono convexo que cumple la propiedad del enunciado pero no sabemos si las diagonales se cortan en el mismo punto. Estas diagonales dividen al hexágono en siete regiones de áreas $S_0,\ldots,S_6$ y denotamos por $a_1,a_2,a_3$, $b_1,b_2,b_3$ y $x_1,x_2,x_3$ los segmentos que se forman, todo ello como se indica en la figura. Las igualdades de las áreas se traducen en \begin{align*} S_1+S_2+S_3&=S_0+S_4+S_5+S_6,\\ S_3+S_4+S_5&=S_0+S_6+S_1+S_2,\\ S_5+S_6+S_1&=S_0+S_2+S_3+S_4. \end{align*} Sumando estas igualdades dos a dos, obtenemos que \[S_1=S_0+S_4,\qquad S_2=S_0+S_5,\qquad S_3=S_0+S_6,\] Tenemos que $S_1$ es el área de un triángulo que se puede calcular como la mitad del producto de $a_1$ y $a_2$ por el seno del ángulo que forman estos dos lados y que $S_0+S_4$ es el área de otro triángulo que análogamente es la mitad del producto de $x_1+b_1$ y $x_2+b_2$ por el seno del ángulo que forman estos dos segmentos. Los dos ángulos que se han considerado son opuestos por el vértice luego sus senos pueden simplificarse en la igualdad $S_1=S_0+S_4$, obteniendo que \[S_1=S_0+S_4\ \Longleftrightarrow\ a_1a_2=(b_1+x_1)(b_2+x_2)\] y de la misma forma \begin{align*} S_2=S_0+S_5&\ \Longleftrightarrow\ a_3b_1=(b_3+x_3)(a_1+x_1), S_3=S_0+S_6&\ \Longleftrightarrow\ b_2b_3=(a_2+x_2)(a_3+x_3). \end{align*} Multiplicando las tres igualdades así obtenidas, llegamos a que \[a_1a_2a_3b_1b_2b_3=(a_1+x_1)(a_2+x_2)(a_3+x_3)(b_1+x_1)(b_2+x_2)(b_3+x_3),\] pero como todos los números son positivos, el miembro de la derecha es estrictamente mayor que el de la izquierda a menos que $x_1=x_2=x_3=0$, lo que equivale a que las tres diagonales se corten en un único punto.

Solución. Supongamos que $d\geq 2$ es un divisor común a $m^2+n^2$ y $m+n$. Entonces también es un divisor de $(m+n)^2-(m^2+n^2)=2mn$ pero no puede ser divisor de $m$ ni de $n$ (al ser divisor de $m+n$, si lo fuera también de $m$, lo sería de $n=(m+n)-m$, pero $m$ y $n$ son primos relativos). Por lo tanto, $d$ debe dividir a $2$ y no queda otra que $d=2$.

Como el máximo común divisor de $m+n$ y $m^2+n^2$ es, en particular, un divisor común, tiene que ser $1$ o $2$. Será igual a $2$ cuando $m$ y $n$ tengan la misma paridad y $1$ cuando tengan distinta paridad.

Solución. Consideremos únicamente las rectas que forman la cuadrícula del tablero, que son paralelas a los lados del tablero y son las únicas que pueden no atravesar ninguna ficha. Si una de estas rectas cortara a un número impar de fichas, entonces, quitando esas fichas, a cada lado de la recta quedaría un número impar de casillas que cubrir con fichas $2\times 1$, lo cual es imposible. Esto prueba que cada una de las rectas atraviesa a un número par de fichas. Para probar (a), razonamos por reducción al absurdo suponiendo que cada uno de las 10 rectas a considerar atraviesa a alguna ficha. Como cada una de ellas atraviesa un número par de fichas y cada ficha es cortada por un sola recta, tendría que haber, al menos, 20 fichas distintas. Esto es imposible ya que sólo tenemos 18 fichas para rellenar el tablero $6\times 6$.

El mismo argumento no funciona para un tablero $8\times 8$ y es que sí que es posible rellenarlo con fichas de dominó, como se muestra en la figura. El razonamiento anterior nos da una pista ya que de las 14 rectas a considerar, podemos tomar 12 de ellas que cortan a 2 fichas cada una y las 2 restantes a 4 fichas cada una, lo que nos da las $12\cdot 2+2\cdot 4=32$ fichas.

Solución. Cada equipo juega un total de 7 partidos luego se lleva como máximo 14 puntos. Por un lado, no puede haber dos equipos con 13 y 14 puntos, puesto que entonces querría decir que el de 14 le ha ganado a todos (en particular, al que ha sacado 13), pero el que tiene 13 ha ganado a todos salvo a uno con el que ha empatado. Esto nos dice que el segundo clasificado tiene como máximo 12 puntos. Por otro lado, si nos fijamos en los cuatro equipos con menos puntos, han jugado entre sí un total de 6 partidos en los que se han repartido 12 puntos, luego estos cuatro equipos tienen una suma de al menos 12 puntos. Con la condición del enunciado deducimos que el segundo clasificado tiene 12 puntos y que los cuatro equipos con menos puntos han perdido todos sus partidos contra los cuatro equipos con más puntos. Por lo tanto, el equipo que quedó en tercer lugar ganó contra el equipo que quedó en séptimo lugar.

Solución. Supongamos que $n^2$ es un elemento de la sucesión. Llamando $d\in\mathbb{N}$ a su diferencia, todos los términos a partir de $n^2$ serán de la forma $n^2+ad$ con $a\in\mathbb{N}$, por lo que $(n+d)^2=n^2+(2n+d)d$ es otro cuadrado en la sucesión y es mayor que $n^2$. Esto implica claramente que la sucesión contiene infinitos cuadrados.

Solución. Supongamos que colocamos todos los dígitos del $0$ al $9$ de cualquier forma en los vértices del $45$-góno. Alguno de ellos estará colocado en menos de $5$ vértices ya que hay $10$ dígitos distintos y sólo $45$ vértices. Esto quiere decir que ese dígito $n$ compartirá segmento con otros $8$ dígitos como máximo y, por tanto, existirá otro dígito $m$ de forma que $m$ y $n$ no son los dos extremos de un mismo segmento.

Ahora bien, hay $\binom{10}{2}=45$ posibles combinaciones de dos dígitos distintos y una de ellas no se toma nunca según hemos visto. Deducimos que la respuesta a la pregunta es negativa.

Solución. Para el apartado (a), sea $ABCD$ un cuadrilátero convexo y $P$ el punto de corte de sus diagonales. Si llamamos $X$ e $Y$ las proyecciones de $A$ y $C$ sobre la diagonal $BD$, debe cumplirse que $AX=CY$ para que los triángulos $ABD$ y $BCD$ tienen la misma área (observemos que $BD$ actúa como base común de ambos triángulos). Como $AXP$ y $CYP$ son semejantes por estar en posición de Thales, se sigue que son congruentes y $AP=CP$. De la misma forma se prueba que $BP=DP$, luego las diagonales de $ABCD$ se cortan en su punto medio y el cuadrilátero tiene que ser un paralelogramo.

En cuanto al apartado (b), supongamos que tenemos un hexágono convexo que cumple la propiedad del enunciado pero no sabemos si las diagonales se cortan en el mismo punto. Estas diagonales dividen al hexágono en siete regiones de áreas $S_0,\ldots,S_6$ y denotamos por $a_1,a_2,a_3$, $b_1,b_2,b_3$ y $x_1,x_2,x_3$ los segmentos que se forman, todo ello como se indica en la figura. Las igualdades de las áreas se traducen en \begin{align*} S_1+S_2+S_3&=S_0+S_4+S_5+S_6,\\ S_3+S_4+S_5&=S_0+S_6+S_1+S_2,\\ S_5+S_6+S_1&=S_0+S_2+S_3+S_4. \end{align*} Sumando estas igualdades dos a dos, obtenemos que \[S_1=S_0+S_4,\qquad S_2=S_0+S_5,\qquad S_3=S_0+S_6,\] Tenemos que $S_1$ es el área de un triángulo que se puede calcular como la mitad del producto de $a_1$ y $a_2$ por el seno del ángulo que forman estos dos lados y que $S_0+S_4$ es el área de otro triángulo que análogamente es la mitad del producto de $x_1+b_1$ y $x_2+b_2$ por el seno del ángulo que forman estos dos segmentos. Los dos ángulos que se han considerado son opuestos por el vértice luego sus senos pueden simplificarse en la igualdad $S_1=S_0+S_4$, obteniendo que \[S_1=S_0+S_4\ \Longleftrightarrow\ a_1a_2=(b_1+x_1)(b_2+x_2)\] y de la misma forma \begin{align*} S_2=S_0+S_5&\ \Longleftrightarrow\ a_3b_1=(b_3+x_3)(a_1+x_1), S_3=S_0+S_6&\ \Longleftrightarrow\ b_2b_3=(a_2+x_2)(a_3+x_3). \end{align*} Multiplicando las tres igualdades así obtenidas, llegamos a que \[a_1a_2a_3b_1b_2b_3=(a_1+x_1)(a_2+x_2)(a_3+x_3)(b_1+x_1)(b_2+x_2)(b_3+x_3),\] pero como todos los números son positivos, el miembro de la derecha es estrictamente mayor que el de la izquierda a menos que $x_1=x_2=x_3=0$, lo que equivale a que las tres diagonales se corten en un único punto.

Solución. Cada equipo juega un total de 7 partidos luego se lleva como máximo 14 puntos. Por un lado, no puede haber dos equipos con 13 y 14 puntos, puesto que entonces querría decir que el de 14 le ha ganado a todos (en particular, al que ha sacado 13), pero el que tiene 13 ha ganado a todos salvo a uno con el que ha empatado. Esto nos dice que el segundo clasificado tiene como máximo 12 puntos. Por otro lado, si nos fijamos en los cuatro equipos con menos puntos, han jugado entre sí un total de 6 partidos en los que se han repartido 12 puntos, luego estos cuatro equipos tienen una suma de al menos 12 puntos. Con la condición del enunciado deducimos que el segundo clasificado tiene 12 puntos y que los cuatro equipos con menos puntos han perdido todos sus partidos contra los cuatro equipos con más puntos. Por lo tanto, el equipo que quedó en tercer lugar ganó contra el equipo que quedó en séptimo lugar.

Solución. Si hacemos $x=\frac{1}{2}$, nos queda $-(\frac{a}{2}+b)^{20}=(\frac{1}{4}+\frac{p}{2}+q)^{10}$, pero esto implica que ambos miembros deben ser cero ya que el de la izquierda es menor o igual que cero y el de la derecha mayor o igual que cero. Por lo tanto, deducimos que $b=\frac{-a}{2}$. Ahora bien, el coeficiente de grado $20$ en la ecuación original nos da la igualdad $2^{20}-a^{20}=1$, de donde $a=\sqrt[20]{2^{20}-1}$ y $b=-\sqrt[20]{1-2^{-20}}$. Tenemos entonces que \begin{align*} (2x-1)^{20}-(ax+b)^{20}&=2^{20}(x-\tfrac{1}{2})^{20}-a^{20}(x-\tfrac{1}{2})^{20}\\ &=(x-\tfrac{1}{2})^{20}=(x^2-x+\tfrac{1}{4})^{10}, \end{align*} luego concluimos que necesariamente $p=-1$ y $q=\frac{1}{4}$.

Solución. Cada equipo juega un total de 7 partidos luego se lleva como máximo 14 puntos. Por un lado, no puede haber dos equipos con 13 y 14 puntos, puesto que entonces querría decir que el de 14 le ha ganado a todos (en particular, al que ha sacado 13), pero el que tiene 13 ha ganado a todos salvo a uno con el que ha empatado. Esto nos dice que el segundo clasificado tiene como máximo 12 puntos. Por otro lado, si nos fijamos en los cuatro equipos con menos puntos, han jugado entre sí un total de 6 partidos en los que se han repartido 12 puntos, luego estos cuatro equipos tienen una suma de al menos 12 puntos. Con la condición del enunciado deducimos que el segundo clasificado tiene 12 puntos y que los cuatro equipos con menos puntos han perdido todos sus partidos contra los cuatro equipos con más puntos. Por lo tanto, el equipo que quedó en tercer lugar ganó contra el equipo que quedó en séptimo lugar.

Solución. Al insertar entre cada dos números su suma, a la suma de todos los números le estamos sumando ambos números. Como cada número del paso $n$ aparece en dos sumas nuevas del paso $n+1$, en total habremos sumado todos los números dos veces. Si llamamos $S_n$ a la suma de los números en el paso $n$, tendremos entonces que $S_{n+1}=S_n+2S_n=3S_n$. Ahora bien, en el paso $1$ tenemos que $S_1=1+1=2$, luego se sigue claramente que $S_{n}=2\cdot 3^{n-1}$.

Nota. En realidad, cambiar la cantidad de números iniciales o sus valores sólo afecta a $S_1$, de forma que la fórmula $S_{n}=3^{n-1}S_1$ es independiente de la configuración inicial.

Solución. Para el apartado (a), sea $ABCD$ un cuadrilátero convexo y $P$ el punto de corte de sus diagonales. Si llamamos $X$ e $Y$ las proyecciones de $A$ y $C$ sobre la diagonal $BD$, debe cumplirse que $AX=CY$ para que los triángulos $ABD$ y $BCD$ tienen la misma área (observemos que $BD$ actúa como base común de ambos triángulos). Como $AXP$ y $CYP$ son semejantes por estar en posición de Thales, se sigue que son congruentes y $AP=CP$. De la misma forma se prueba que $BP=DP$, luego las diagonales de $ABCD$ se cortan en su punto medio y el cuadrilátero tiene que ser un paralelogramo.

En cuanto al apartado (b), supongamos que tenemos un hexágono convexo que cumple la propiedad del enunciado pero no sabemos si las diagonales se cortan en el mismo punto. Estas diagonales dividen al hexágono en siete regiones de áreas $S_0,\ldots,S_6$ y denotamos por $a_1,a_2,a_3$, $b_1,b_2,b_3$ y $x_1,x_2,x_3$ los segmentos que se forman, todo ello como se indica en la figura. Las igualdades de las áreas se traducen en \begin{align*} S_1+S_2+S_3&=S_0+S_4+S_5+S_6,\\ S_3+S_4+S_5&=S_0+S_6+S_1+S_2,\\ S_5+S_6+S_1&=S_0+S_2+S_3+S_4. \end{align*} Sumando estas igualdades dos a dos, obtenemos que \[S_1=S_0+S_4,\qquad S_2=S_0+S_5,\qquad S_3=S_0+S_6,\] Tenemos que $S_1$ es el área de un triángulo que se puede calcular como la mitad del producto de $a_1$ y $a_2$ por el seno del ángulo que forman estos dos lados y que $S_0+S_4$ es el área de otro triángulo que análogamente es la mitad del producto de $x_1+b_1$ y $x_2+b_2$ por el seno del ángulo que forman estos dos segmentos. Los dos ángulos que se han considerado son opuestos por el vértice luego sus senos pueden simplificarse en la igualdad $S_1=S_0+S_4$, obteniendo que \[S_1=S_0+S_4\ \Longleftrightarrow\ a_1a_2=(b_1+x_1)(b_2+x_2)\] y de la misma forma \begin{align*} S_2=S_0+S_5&\ \Longleftrightarrow\ a_3b_1=(b_3+x_3)(a_1+x_1), S_3=S_0+S_6&\ \Longleftrightarrow\ b_2b_3=(a_2+x_2)(a_3+x_3). \end{align*} Multiplicando las tres igualdades así obtenidas, llegamos a que \[a_1a_2a_3b_1b_2b_3=(a_1+x_1)(a_2+x_2)(a_3+x_3)(b_1+x_1)(b_2+x_2)(b_3+x_3),\] pero como todos los números son positivos, el miembro de la derecha es estrictamente mayor que el de la izquierda a menos que $x_1=x_2=x_3=0$, lo que equivale a que las tres diagonales se corten en un único punto.