Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
IV All-Soviet-Union Mathematical Competitions — 1964
Sesión 1 — Nivel 8
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Hemos probado que llegamos siempre a una sucesión constante $a\in\mathbb{Z}$, pero en el paso anterior a esta constante, los números deben ser alternadamente $a+r$ y $a-r$ para otro entero $r$. La sucesión no puede alternar cíclicamente entre dos valores si el número de elementos $n$ es impar.
Nota. Si $n=2k$ es par, sí que podrían ser distintos los números, aunque sigue siendo cierto que la sucesión es finalmente constante. Por ejemplo, si $a_1=a_3=\ldots=a_{2k-1}=1$ y $a_2=a_4=\ldots=a_{2k}=3$, siempre obtenemos números enteros y los números originales no son todos iguales.
Informar de error en enunciado Informar de procedencia del problema
- Un hexágono $ABCDEF$ tiene todos sus ángulos iguales. Demostrar que \[AB-DE=EF-BC=CD-FA.\]
- Dados seis números reales positivos $a_1,\ldots, a_6$ tales que $a_1-a_4=a_5-a_2=a_3-a_6$, demostrar que se puede construir un hexágono con lados de longitudes $a_1,\ldots,a_6$ y ángulos iguales.
Informar de error en enunciado Informar de procedencia del problema
Sesión 2
Sesión 3 — Nivel 9
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
- Demostrar que recorre al menos una distancia $\frac{1}{2}AB$ en una de las tres direcciones determinadas por los lados de los hexágonos.
- Si recorre exactamente una distancia $\frac{1}{2}AB$ en la misma dirección, ¿cuántas aristas recorre en total?
Informar de error en enunciado Informar de procedencia del problema
Sesión 4
Sesión 5 — Nivel 10
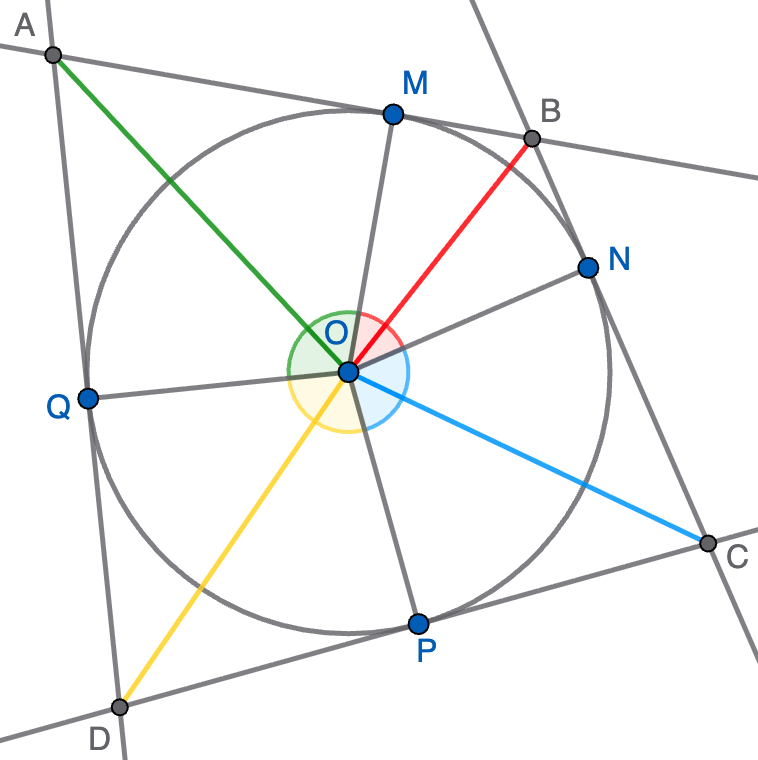
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
- Un hexágono $ABCDEF$ tiene todos sus ángulos iguales. Demostrar que \[AB-DE=EF-BC=CD-FA.\]
- Dados seis números reales positivos $a_1,\ldots, a_6$ tales que $a_1-a_4=a_5-a_2=a_3-a_6$, demostrar que se puede construir un hexágono con lados de longitudes $a_1,\ldots,a_6$ y ángulos iguales.
Informar de error en enunciado Informar de procedencia del problema
- Si todos los elementos $a_3,\ldots,a_n$ están en el denominador, entonces podemos los poner paréntesis para hacer las divisiones en orden: \[((((a_1/a_2)/a_3)/\ldots)/a_n=\frac{a_1}{a_2a_3\cdots a_n}.\]
- Si no todos los elementos $a_3,\ldots,a_n$ están en el denominador, entonces habrá un primer índice $k\geq 2$ para el que $a_k$ está en el denominador y $a_{k+1}$ en el numerador. Entonces, podemos poner paréntesis de la forma $(A)/(B)$. En $A$ están los números $a_1,a_2,\ldots,a_{k-1}$ con los paréntesis necesarios para obtener la misma disposición que en ($\star$), lo cual se consigue usando la hipótesis de inducción. Análogamente, en $B$ están los números $a_k,\ldots,a_n$ con paréntesis para obtener la misma disposición que en ($\star$) cambiando numerador por denominador, lo que de nuevo es posible por la hipótesis de inducción. De esta forma, la expresión $(A)/(B)$ es algebraicamente equivalente a ($\star$).
Como hay total libertad para elegir las posiciones (numerador o denominador) de $n-2$ números (del $a_3$ al $a_n$), concluimos que hay un total de $2^{n-2}$ expresiones distintas.
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Sesión 6 — Nivel 11
- Hallar el menor cuadrado perfecto de al menos tres cifras cuyo dígito de las unidades no es cero y que es de nuevo un cuadrado al borrar sus dígitos de las decenas y las unidades.
- Hallar todos los cuadrados perfectos que no contienen los dígitos 0 ni 5 tales que, si su segundo dígito (por la izquierda) se elimina, el número resultante divide al original.
Informar de error en enunciado Informar de procedencia del problema
Los triángulos $BEC$ y $AED$ son congruentes, luego $r_4=r_2$. Los triángulos $AEB$ y $CED$ son semejantes ya que $AB$ y $CD$ son paralelas y están en proporción $2-x$ a $x$. En consecuencia, tenemos que $r_1=\frac{2-x}{x}r_3$, lo que nos permite reescribir la condición del enunciado como: \[\frac{1}{r_1}+\frac{1}{r_3}=\frac{1}{r_2}+\frac{1}{r_4}\ \Leftrightarrow\ r_2=(2-x)r_3.\] Sea $P$ el pie de la perpendicular por $D$ al lado $AB$. El teorema de Pitágoras en el triángulo $APD$ nos dice que $1=AP^2+DP^2=(1-x)^2+DP^2$ y en el triángulo $BDP$ nos dice que $BD^2=DP^2+BP^2=DP^2+1$. De estas dos ecuaciones, se deduce que $DP^2=1+2x-x^2$, luego se tiene por la semejanza entre $CED$ y $AEB$ que \[DE=\frac{x}{2}DP=\frac{x}{2}\sqrt{1+2x-x^2},\qquad BE=\frac{2-x}{2}DP=\frac{2-x}{2}\sqrt{1+2x-x^2}.\] Para obtener la relación entre $r_2$ y $r_3$, usamos que el área de un triángulo es igual al semiperímetro por el radio inscrito en los triángulos $BEC$ y $CED$, que tienen por altura común $h$ a la perpendicular por $C$ a $DB$. En el triángulo $BEC$, tenemos que \[\tfrac{1}{2}(1+\sqrt{1+2x-x^2})r_2=\tfrac{1}{2}BE\cdot h=\frac{2-x}{4}\sqrt{1+2x-x^2}\cdot h,\] mientras que en el triángulo $CED$ obtenemos \[\tfrac{1}{2}(x+x\sqrt{1+2x-x^2})r_3=\tfrac{1}{2}DE\cdot h=\frac{x}{4}\sqrt{1+2x-x^2}\cdot h.\] Despejando e igualando $h$ en ambas fórmulas, se tiene que $r_2=(2-x)r_3$, como queríamos demostrar.
Informar de error en enunciado Informar de procedencia del problema
- Si todos los elementos $a_3,\ldots,a_n$ están en el denominador, entonces podemos los poner paréntesis para hacer las divisiones en orden: \[((((a_1/a_2)/a_3)/\ldots)/a_n=\frac{a_1}{a_2a_3\cdots a_n}.\]
- Si no todos los elementos $a_3,\ldots,a_n$ están en el denominador, entonces habrá un primer índice $k\geq 2$ para el que $a_k$ está en el denominador y $a_{k+1}$ en el numerador. Entonces, podemos poner paréntesis de la forma $(A)/(B)$. En $A$ están los números $a_1,a_2,\ldots,a_{k-1}$ con los paréntesis necesarios para obtener la misma disposición que en ($\star$), lo cual se consigue usando la hipótesis de inducción. Análogamente, en $B$ están los números $a_k,\ldots,a_n$ con paréntesis para obtener la misma disposición que en ($\star$) cambiando numerador por denominador, lo que de nuevo es posible por la hipótesis de inducción. De esta forma, la expresión $(A)/(B)$ es algebraicamente equivalente a ($\star$).
Como hay total libertad para elegir las posiciones (numerador o denominador) de $n-2$ números (del $a_3$ al $a_n$), concluimos que hay un total de $2^{n-2}$ expresiones distintas.
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema