Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
X All-Soviet-Union Mathematical Competitions — 1976
Sesión 1 — Nivel 8 (primer día)
Informar de error en enunciado Informar de procedencia del problema
- Demostrar que las filas $11$ y $12$ son idénticas
- Demostrar que las filas $10$ y $11$ no tienen por qué ser idénticas.
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Sesión 2 — Nivel 8 (segundo día)
- Cada escarabajo puede aterrizar en una nueva casilla o caer en la que estaba.
- Más de un escarabajo puede aterrizar en la misma casilla.
- Si dos escarabajos estaban en la misma casilla o en casillas que comparten algún vértice, después aterrizan en la misma casilla o en casillas que comparten un vértice.
- $S$ es el conjunto formado por las casillas de la fila y columna centrales.
- $S$ es el conjunto formado por las casillas de la fila y columna centralres junto con las casillas del borde del tablero.
- $S$ es todo el tablero.
Informar de error en enunciado Informar de procedencia del problema
- Demostrar que se puede descomponer un triángulo equilátero de lado $5$ en $100$ triángulos grandes que sean disjuntos o bien tenga intersección un vértice o un lado común.
- Demostrar que también se puede descomponer un triángulo equilátero de lado $3$ en las mismas condiciones.
Informar de error en enunciado Informar de procedencia del problema
- Dar un ejemplo de sucesión universal de $n^2$ elementos.
- Dar un ejemplo de sucesión universal de $n^2-n+1$ elementos.
- Demostrar que cualquier sucesión universal contiene al menos $\frac{n(n+1)}{2}$ elementos.
- Demostrar que la sucesión universal más corta para $n=4$ contiene $12$ elementos.
Nota. En el problema original también se proponía encontrar la longitud óptima de la sucesión universal para todo $n$. Este se daba como un problema abierto y se indicaba que la mejor cota superior encontrada por el comité organizador de la olimpiada es $n^2-2n+4$ elementos.
Informar de error en enunciado Informar de procedencia del problema
Sesión 3 — Nivel 9 (primer día)
Informar de error en enunciado Informar de procedencia del problema
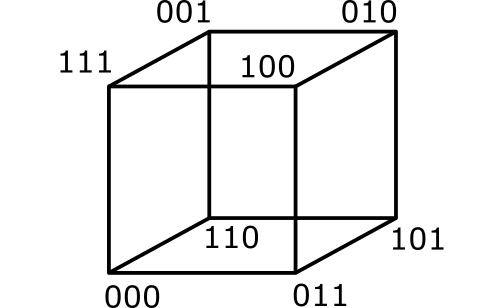
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Sesión 4 — Nivel 9 (segundo día)
- Demostrar que se puede descomponer un triángulo equilátero de lado $5$ en $100$ triángulos grandes que sean disjuntos o bien tenga intersección un vértice o un lado común.
- Demostrar que también se puede descomponer un triángulo equilátero de lado $3$ en las mismas condiciones.
Informar de error en enunciado Informar de procedencia del problema
- Probar que hay dos números consecutivos cuya diferencia es menor o igual que $\frac{n}{4}$.
- Probar que existe un número que difiere de la media aritmética de sus dos vecinos al menos $\frac{8}{n^2}$.
- Mejorar la estimación del apartado (b) sustituyendo $8$ por un valor mayor.
- Demostrar que, para $n=30$, hay un número que difieren de la media aritmética de sus dos vecinos al menos $\frac{2}{113}$ y de un ejemplo de de $30$ números tales que ninguno de ellos difiere de la media aritmética de sus vecinos más de $\frac{2}{113}$.
Informar de error en enunciado Informar de procedencia del problema
- Dar un ejemplo de sucesión universal de $n^2$ elementos.
- Dar un ejemplo de sucesión universal de $n^2-n+1$ elementos.
- Demostrar que cualquier sucesión universal contiene al menos $\frac{n(n+1)}{2}$ elementos.
- Demostrar que la sucesión universal más corta para $n=4$ contiene $12$ elementos.
Nota. En el problema original también se proponía encontrar la longitud óptima de la sucesión universal para todo $n$. Este se daba como un problema abierto y se indicaba que la mejor cota superior encontrada por el comité organizador de la olimpiada es $n^2-2n+4$ elementos.
Informar de error en enunciado Informar de procedencia del problema
Sesión 5 — Nivel 10 (primer día)
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Sesión 6 — Nivel 10 (segundo día)
- Demostrar que para cualquier $n\gt 2$ podemos etiquetar los vértices de forma que no se puede pasar a que todos sean $+1$ mediante una serie de movimientos.
- Si $f(n)$ es el mayor número de etiquetados iniciales que podemos encontrar para los que ninguno de ellos se puede obtener de ningún otro mediante una serie de movimientos, demostrar que $f(200)=2^{80}$.
Informar de error en enunciado Informar de procedencia del problema
- Demostrar que si $x,y,z$ son los extremos de tres radios de $S$ mutuamente perpendiculares, entonces $f(x)^2+f(y)^2+f(z)^2=1$.
- Sea $g:S\to\mathbb{R}$ una función que toma valores mayores o iguales que $0$ y cumple que $g(x)^2+g(y)^2+g(z)^2=1$ para cualesquiera extremos de radios de $S$ mutuamente perpendiculares. Si $g(x)=1$ siempre que $f(x)=1$, demostrar que $g(x)=f(x)$ para todo $x\in S$.
Informar de error en enunciado Informar de procedencia del problema
- Dar un ejemplo de sucesión universal de $n^2$ elementos.
- Dar un ejemplo de sucesión universal de $n^2-n+1$ elementos.
- Demostrar que cualquier sucesión universal contiene al menos $\frac{n(n+1)}{2}$ elementos.
- Demostrar que la sucesión universal más corta para $n=4$ contiene $12$ elementos.
Nota. En el problema original también se proponía encontrar la longitud óptima de la sucesión universal para todo $n$. Este se daba como un problema abierto y se indicaba que la mejor cota superior encontrada por el comité organizador de la olimpiada es $n^2-2n+4$ elementos.
Informar de error en enunciado Informar de procedencia del problema