Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
II Olimpiada Iberoamericana de Matemáticas — 1987
Sesión 1 — 28 de enero de 1987
La ecuación inicial se puede escribir como $f(x)^2f(\varphi(x))=64x$. Si sustituimos $x$ por $\varphi(x)$, obtenemos que $f(\varphi(x))^2\cdot f(x)=64\varphi(x)$, con lo cual tenemos el sistema \[\left\{\begin{array}{l}f(x)^2f(\varphi(x))=64x,\\f(\varphi(x))^2 f(x)=64\varphi(x).\end{array}\right.\] Elevando la primera igualdad al cuadrado y dividiéndola por la segunda (que no se anula ya que $x\neq\pm 1$, luego $\varphi(x)\neq 0$) llegamos a que $f(x)^3=64\frac{x^2}{\varphi(x)}$, de donde podemos despejar \[f(x)=\sqrt[3]{\frac{64x^2}{\varphi(x)}}=4\sqrt[3]{\frac{x^2(1+x)}{1-x}}.\] Puede comprobarse que esta función está bien definida para $x\neq-1$ y satisface la igualdad del enunciado, luego es la única solución al problema.
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Esto termina de probar que $a_r=1+c_r^2$ para todo $r\in\mathbb{N}$, con lo que el enunciado está demostrado.
Nota. Sin duda el paso más difícil en esta demostración es sacarse de la manga la sucesión $c_r$. Si uno intuye que la $c_r$ debe cumplir una recurrencia lineal del tipo $c_r=\alpha c_{r-1}+\beta c_{r-2}$, pueden calcularse algunos términos para ver que ha de ser $\alpha=4$ y $\beta=-1$.
Informar de error en enunciado Informar de procedencia del problema
Sesión 2 — 29 de enero de 1987
Informar de error en enunciado Informar de procedencia del problema
- Demostrar que $r$, $s$ y $t$ son positivas.
- Calcular $\arctan(r)+\arctan(s)+\arctan(t)$.
Para el segundo apartado, vamos a hacer uso de la fórmula de la tangente del la suma. Concretamente, dados $x,y,z\in(0,\frac{\pi}{2})$, de dicha fórmula se deduce que \[\mathrm{tg}(x+y+z)=\frac{\mathrm{tg}(x+y)+\mathrm{tg}(z)}{1-\mathrm{tg}(x+y)\mathrm{tg}(z)}=\frac{\mathrm{tg}(x)+\mathrm{tg}(y)+\mathrm{tg}(z)-\mathrm{tg}(x)\mathrm{tg}(y)\mathrm{tg}(z)}{1-\mathrm{tg}(x)\mathrm{tg}(y)-\mathrm{tg}(y)\mathrm{tg}(z)-\mathrm{tg}(z)\mathrm{tg}(x)}.\] Sustituyendo $x=\mathrm{arctg}(r)$, $y=\mathrm{arctg}(s)$ y $z=\mathrm{arctg}(t)$, tenemos que \[\mathrm{tg}(\mathrm{arctg}(r)+\mathrm{arctg}(s)+\mathrm{arctg}(t))=\frac{(r+s+t)-rst}{1-(rs+st+rt)}=\frac{\frac{13}{3}-\frac{2}{3}}{1-\frac{14}{3}}=-1.\] ya que las relaciones de Cardano para el polinomio $p(x)$ nos aseguran que \[ r+s+t=\frac{13}{3},\quad rs+st+rt=\frac{14}{3},\quad rst=\frac{2}{3}. \] Esto nos dice que existe un número entero $k$ tal que \[\mathrm{arctg}(r)+\mathrm{arctg}(s)+\mathrm{arctg}(t)=-\frac{\pi}{4}+k\pi.\] Como $r,s,t\gt 0$, tenemos que $0\lt \mathrm{arctg}(r)+\mathrm{arctg}(s)+\mathrm{arctg}(t)\lt\frac{3\pi}{2}$, de donde $k=1$ y \[\mathrm{arctg}(r)+\mathrm{arctg}(s)+\mathrm{arctg}(t)=\frac{3\pi}{4}.\]
Informar de error en enunciado Informar de procedencia del problema
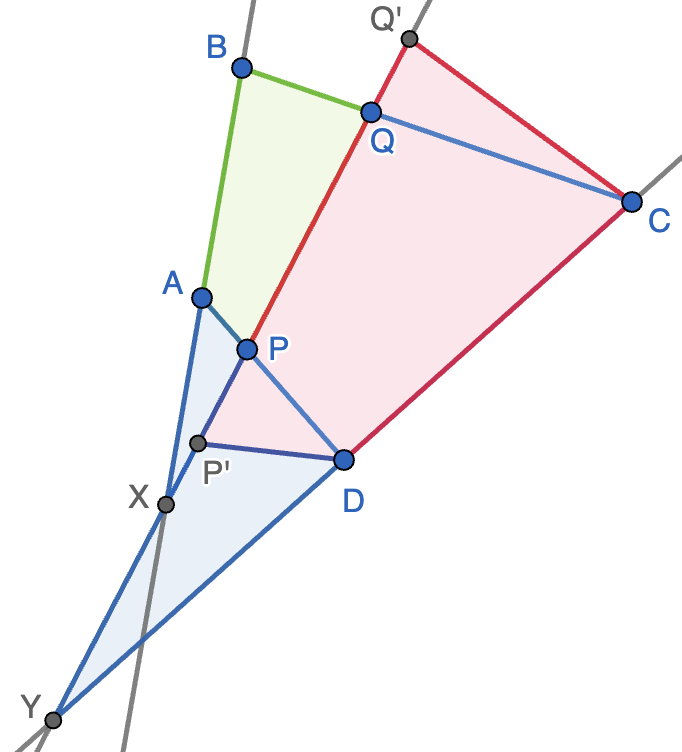
Informar de error en enunciado Informar de procedencia del problema