Olimpiadas de Matemáticas
Página de preparación y problemas

Solución. Supongamos que las longitudes de los lados son $a=\ell-d$, $b=\ell$ y $c=\ell+d$, siendo $\ell\gt 0$ y $d\geq 0$. Si llamamos $S$ al área del triángulo, sabemos que \[2S=a\cdot h_a=b\cdot h_b=c\cdot h_c.\] Esto nos dice que las alturas están ordenadas en orden opuesto al de los lados, es decir, $h_a=x+k$, $h_b=x$ y $h_c=x-k$ para ciertos $x\gt 0$ y $k\geq 0$. Usando la fórmula anterior del área, tenemos que \[\ell x-dx+\ell k- dk=(\ell-d)(x+k)=\ell x=(\ell+d)(x-k)=\ell x+dx-\ell k-dk.\] Podemos restar $\ell x-kd$ y queda \[\ell k-dx=dk=-(\ell k-dx),\] y deducimos que $dk=0$. Por tanto, $d=0$, de donde es inmediato que $a=b=c$ y el triángulo es equilátero; o bien $k=0$, de donde $h_a=h_b=h_c$ y el triángulo también es equilátero.

Solución. Escribamos $p=a+c+u$ y $q=b+d+v$ para ciertos enteros $u$ y $v$. La desigualdad $\frac{a}{b}\gt\frac{p}{q}=\frac{a+c+u}{b+d+v}$ nos dice que $ab+ad+av\gt ab+bc+bu=ab+ad-1+bu$. Simplificando, llegamos a que $av\gt bu-1$ y, como estamos trabajando con enteros, tenemos que $av\geq bu$. De la misma forma, usando la desigualdad $\frac{p}{q}\gt\frac{c}{d}$ del enunciado se llega a que $du\geq cv$. Despejando $u$ en estas desigualdades (ya que $b$ y $d$ son positivos) tenemos finalmente que \[\frac{a}{b}v\geq u\geq\frac{c}{d} v.\] En primer lugar, observamos que si $v\lt 0$ (es decir, $q\lt b+d$) entonces llegamos a una contradicción ya que $\frac{a}{b}v\lt\frac{c}{d}v$ y las desigualdades anteriores no se satisfacen para ningún entero $u$. Por tanto, $v\geq 0$ y tenemos probado el apartado (a).

Finalmente, si $q=b+d$, entonces $v=0$, luego las desigualdades arriba probadas nos dicen que $0\geq u\geq 0$ y, por tanto, $u=0$ y $p=a+c$, demostrando así el apartado (b).

Solución. Comenzaremos demostrando que si el triángulo $ABC$ es el de mayor perímetro, entonces $P$ es el incentro. Para ello, vamos a fijar los vértices $B$ y $C$ y mover el vértice $A$ entre todos los puntos de la circunferencia $\Gamma$ de centro $P$ y radio $r$ ($r$ será igual a $3$, $5$ o $7$). Por tanto, el lado $BC$ queda fijo y la suma de distancias $AB+AC$ será constante en cada elipse de focos $B$ y $C$ (por definición de elipse). Si consideramos todas estas elipses, como se muestra en la figura, existirá un punto $Q$ de $\Gamma$ con $QB+QC$ máximo, que se corresponderá con una elipse $E$ tangente en $Q$ a la circunferencia $\Gamma$, como puede verse en la figura (es decir, la elipse de mayor excentricidad que deja a $\Gamma$ en su interior). Observamos que $PQ$ es perpendicular a $\Gamma$ en $Q$ por tratarse de un radio, luego también es perpendicular a $E$ en $Q$ ya que $E$ y $\Gamma$ son tangentes en este punto. Ahora usamos la propiedad de que los segmentos que unen un punto de una elipse con el foco tienen por bisectriz la perpendicular en el punto (ver la nota). Por tanto, el punto $Q$ de $\Gamma$ que maximiza el perímetro cumple que $P$ está en la bisectriz interior del ángulo $A$. Si el triángulo $ABC$ maximiza el perímetro, entonces $P$ tiene que ser el incentro.

Puede parecer que lo anterior demuestra el enunciado, pero podría ocurrir que no hay ningún triángulo $ABC$ cuyo incentro $I$ dista $3$, $5$ y $7$ de los vértices. De hecho, no hemos usado estos tres números para el razonamiento anterior. Tomemos los puntos $P,Q,R$ de los lados $AB,BC,CA$, respectivamente, tales que $IP=IQ=IR=r$, el radio de la circunferencia inscrita. Como estos radios son perpendiculares a los correspondientes lados, en función de $r$, los $360º$ del ángulo completo en $I$ se pueden calcular como \begin{align*} 360º&=\angle AIQ+\angle AIR+\angle RIB+\angle BIP+\angle PIC+\angle CIQ\\ &=2\arccos(\tfrac{r}{3})+2\arccos(\tfrac{r}{5})+2\arccos(\tfrac{r}{7}). \end{align*} Es fácil ver que si esta ecuación se cumple, entonces se pueden construir los seis triángulos rectángulos en que se divide $ABC$ y al unirlos tenemos el triángulo $ABC$ con distancias $3$, $5$ y $7$ al incentro. Definimos entonces la función $f:[0,3]\to\mathbb{R}$ como \[f(r)=2\arccos(\tfrac{r}{3})+2\arccos(\tfrac{r}{5})+2\arccos(\tfrac{r}{7}).\] Esta función es continua y estrictamente decreciente con $f(0)=540^\circ$ y \[f(3)=2\arccos(\tfrac{3}{5})+2\arccos(\tfrac{3}{7})\lt 2\arccos(0)+2\arccos(0)=360^\circ.\] El teorema de Bolzano nos asegura que hay un valor de $r$ para el que $f(r)=360^\circ$.

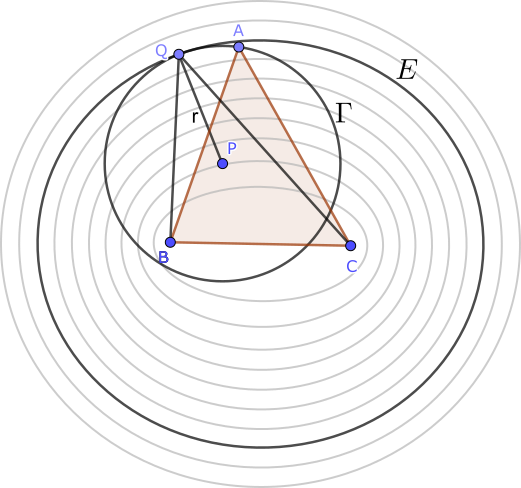
Nota. La propiedad que hemos usado de las elipses es la que hace que, en una sala de planta elíptica, si hablamos en uno de los focos, otra persona oiga con claridad lo que decimos si se sitúa en el otro foco.

Por otro lado, el argumento para la existencia del triángulo no depende realmente de los números $3$, $5$ y $7$ (es decir, se podrían haber escrito otros tres números positivos cualesquiera).

Solución. Comencemos pensando en los $n-1$ segmentos que parten del vértice $A$ y llamémoslos $\ell_1,\ldots,\ell_{n-1}$, siendo $\ell_1$ el más cercano al lado $b$. Si llamamos $P_j$ al extremo de $\ell_j$ sobre el lado $BC$, tendremos que $BP_j=\frac{j}{n}a$ y $CP_j=\frac{n-j}{n}a$. Aplicando el teorema del coseno a los triángulos $ABP_j$ y $ACP_j$, obtenemos las igualdades \begin{eqnarray*} c^2&=&\ell_j^2+\left(\frac{n-j}{n}a\right)^2-2\ell_j\frac{n-j}{n}a\cos(\theta),\\ b^2&=&\ell_j^2+\left(\frac{j}{n}a\right)^2-2\ell_j\frac{j}{n}a\cos(180-\theta), \end{eqnarray*} donde $\theta=\angle AP_jC$. Multiplicando la primera ecuación por $j$ y sumándole la segunda multiplicada por $n-j$ (observamos que $\cos(180-\theta)=-\cos(\theta)$), podemos despejar $\ell_j^2$ como \[\ell_j^2=\frac{j}{n}c^2+\frac{n-j}{n}b^2-\frac{j(n-j)}{n^2}a^2.\] Las siguientes funciones auxiliares: \[r(n)=\sum_{j=1}^{n-1}\frac{j}{n},\qquad s(n)=\sum_{j=1}^{n-1}\frac{j(n-j)}{n^2}\] toman valores racionales y nos permiten escribir \[\sum_{j=1}^{n-1}\ell_j^2=r(n)(b^2+c^2)-s(n)a^2.\] Así tenemos controlada la suma de los cuadrados de las distancias del vértice $A$ a los puntos de división del lado opuesto. Si ahora repetimos el mismo argumento en los otros dos vértices y sumamos las tres cantidades obtenemos \[S=[2r(n)-s(n)](a^2+b^2+c^2).\] Como $2r(n)-s(n)$ es un número racional para todo $n\in\mathbb{N}$, tenemos demostrado el enunciado.

Nota. Realmente, podemos calcular \[r(n)=\sum_{j=1}^{n-1}\frac{j}{n}=\frac{1}{n}\sum_{j=1}^{n-1}j=\frac{n-1}{2}\] \[s(n)=\sum_{j=1}^{n-1}\frac{j(n-j)}{n^2}=\frac{1}{n}\sum_{j=1}^{n-1}j-\frac{1}{n^2}\sum_{j=1}^{n-1}j^2=\frac{n-1}{2}-\frac{(n-1)(2n-1)}{6n},\] lo que nos dice que \[\frac{S}{a^2+b^2+c^2}=2r(n)-s(n)=(n-1)-\frac{n-1}{2}+\frac{(n-1)(2n-1)}{6n}=\frac{(n-1)(5n-1)}{6n}.\]

Solución. Si desarrollamos el producto $(x+yt+zt^2)(u+vt+wt^2)$ usando que $t^3=2$, llegamos el polinomio de segundo grado siguiente: \[[xu+2zv+2yw]+[yu+xv+2zw]t+[zu+yv+xw]t^2\] Vamos a ver que existen $u,v,w\in\mathbb{Q}$ tales que el primer corchete es igual a $1$ y los demás son cero, lo que nos daría el resultado que buscamos. Para ello, escribimos estas tres ecuaciones como \[\left.\begin{array}{r} xu+2zv+2yw=1\\ yu+xv+2zw=0\\ zu+yv+xw=0 \end{array}\right\} \] Nos encontramos así con un sistema de ecuaciones lineales con incógnitas $u,v,w$. Resolviendo este sistema (aquí pueden usarse los métodos de reducción o bien escribirlo matricialmente y usar la regla de Kramer, pero omitimos los detalles por ser algo estándar) llegamos a que el sistema es compatible determinado si, y sólo si, $x^3+2y^3+4z^3-6xyz\neq 0$, en cuyo caso \[\begin{array}{r} u=\frac{x^2-2 y z}{x^3+2 y^3+4 z^3-6 xyz}\\ v=\frac{2 z^2-x y}{x^3+2 y^3+4 z^3-6 xyz}\\ w=\frac{y^2-x z}{x^3+2 y^3+4 z^3-6 xyz} \end{array}\] son números racionales cumpliendo la condición del enunciado. Por tanto, falta por ver que si los racionales $x,y,z$ no son cero a la vez, entonces $x^3+2y^3+4z^3-6xyz\neq 0$ (esta última cantidad puede ser cero para ciertos números reales no nulos --por ejemplo para $x^3=2y^3=4z^3$-- luego habrá que usar fuertemente que se trata de números racionales).

Observamos que si multiplicamos los números $x$, $y$ y $z$ por un número no nulo, entonces $x^3+2y^3+4z^3-6xyz$ queda multiplicado por el cubo de ese número y es cero si, y sólo si, originalmente era cero. Por tanto, no hay pérdida de generalidad en multiplicar $x$, $y$ y $z$ por el mismo entero no nulo. Expresando $x$, $y$ y $z$ como fracción irreducible y multiplicando por el mínimo común múltiplo de los denominadores, podremos suponer sin perder generalidad que $x$, $y$ y $z$ son números enteros sin factores comunes.

Ahora bien, si ocurriera que $x^3+2y^3+4z^3-6xyz=0$, entonces $x$ es par y podemos poner $x=2a$ para cierto entero $a$. La igualdad anterior se reescribe como $4a^3+y^3+2z^3-6ayz=0$, luego $y=2b$ para cierto entero $b$, y podemos volver a reescribirla como $2a^3+4b^3+z^3-6abz=0$, de donde $z$ también es par y hemos encontrado un factor común a $x$, $y$ y $z$ en contra de lo que habíamos supuesto.

Solución. Vamos a razonar por inducción sobre $n$. Para $n=1$, está claro que el conjunto que maximiza la suma de los inversos es $S_1=\{1\}$, luego vamos a suponer que existe un conjunto $S_{n-1}$ de $n-1$ enteros que maximiza la suma de los inversos (de entre todos los subconjuntos de $\mathbb{N}$ con $n-1$ elementos que no tienen tres en progresión artimética) y probar que existe otro conjunto $S_n$ con la misma propiedad para $n$ elementos.

Escribamos los elementos de $S_{n-1}$ como $a_1\lt a_2\lt\ldots\lt a_{n-1}$. Consideremos $\Gamma$ la familia de todos los subconjuntos de $n$ elementos menores o iguales que $2a_{n-1}$ que no tienen tres en progresión artimética. Entonces, $\Gamma$ es una familia finita no vacía puesto que $\{a_1,a_2,\ldots,a_{n-1},2a_{n-1}\}\in\Gamma$. Por tanto, $\Gamma$ tiene (al menos) un elemento cuya suma de inversos es máxima entre todos los elementos de $\Gamma$ y lo definimos como $S_n$. Veamos que $S_n$ tiene suma de inversos mayor que cualquier otro conjunto que no está en $\Gamma$ y habremos terminado. Pongamos que $b_1\lt b_2\lt\ldots\lt b_n$ forman un conjunto de $n$ elementos que no tiene tres en progresión aritmética y que no está en $\Gamma$, luego $b_n\gt 2a_{n-1}$. Esto nos dice que \[\frac{1}{b_1}+\ldots+\frac{1}{b_{n-1}}+\frac{1}{b_n}\leq \frac{1}{b_1}+\ldots+\frac{1}{b_{n-1}}+\frac{1}{2a_n}\leq \frac{1}{a_1}+\ldots+\frac{1}{a_{n-1}}+\frac{1}{2a_n},\] donde hemos usado la hipótesis de inducción. Por tanto, el conjunto $\{b_1,\ldots,b_n\}$ es peor que $\{a_1,\ldots,a_{n-1},2a_{n-1}\}\in\Gamma$, luego tiene suma de inversos menor que la de $S_n$.

Nota. Antes de empezar, es necesario entender el problema, porque podría parecer que es una obviedad. El quid de la cuestión es que hay infinitos conjuntos de $n$ números naturales y en una tal familia infinita podría no haber máximo (la suma de los inversos podría tomar valores arbitrariamente cercanos a cierta cota superior sin alcanzarla nunca). El punto fundamental de la solución dada consiste en ver que el máximo se puede elegir de entre una cantidad finita de sucesiones.