Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
VI Olimpiada Iberoamericana de Matemáticas — 1991
Sesión 1 — 24 de septiembre de 1991
- los cuatro signos pasan de positivos a negativos, con lo que la suma cambia en $-8$;
- pasan de un negativo y tres positivos a un positivo y tres negativos, con lo que la suma cambia en $-4$;
- pasan de dos positivos y dos negativos a dos positivos y dos negativos, con lo que la suma no cambia;
- pasan de un positivo y tres negativos a un negativo y tres positivos, con lo que la suma cambia en $+4$;
- pasan de todos negativos a todos positivos y la suma cambia en $+8$.
Partiendo de todos los signos positivos (con suma igual a $14$) y cambiando vértices de signo, podemos llegar a cualquier configuración pero los casos anteriores nos dicen que la suma será la original modificada en un múltiplo de $4$, es decir, será 14, 10, 6, 2, $-2$, $-6$, $-10$ ó $-14$.
El valor $-14$ no puede ser puesto que implicaría que todos los números son negativos y no pueden ser simultáneamente negativos los cuatro vértices de una cara y la propia cara. Tampoco puede darse el caso $-10$ ya que habría dos números negativos y $12$ positivos. Los demás casos (14, 10, 6, 2, $-2$, $-6$) sí que pueden ocurrir y dejamos al lector que ponga ejemplos de cada uno de ellos.
Informar de error en enunciado Informar de procedencia del problema
La región rotada $A'\cup B'$ tiene área $2$ y está delimitada por $r'$, mientras que $B\cup C$ está delimitada por $s$ paralela a $r'$ y también tiene área $2$. Para que esto ocurra, debe ser necesariamente $r'=s$ (en caso contrario, $A'\cup B'$ estaría estrictamente contenida en $B\cup C$ o viceversa, luego no podrían tener la misma área). Por un argumento similar, la región $B'$ debe coincidir con $C$ para que ambas tengan área $1$ (si no, $B'$ estaría estrictamente contenida en $C$ o viceversa). Por lo tanto, el punto de intersección de $r$ y $s$ debe ser el centro de rotación $O$. Así, $A,B,C,D$ son congruentes mediante rotaciones respecto de $O$ y tienen todas área $1$.

Informar de error en enunciado Informar de procedencia del problema
- $f(0)=0$,
- $f(\frac{x}{3})=\frac{f(x)}{2}$,
- $f(1-x)=1-f(x)$,
Multiplicamos el numerador por la mayor potencia de $3$ posible para no salirnos del intervalo $[0,1]$ y obtenemos usando la segunda regla que \[f\left(\frac{18}{1991}\right)=\frac{1}{2^4}\cdot f\left(\frac{18\cdot 3^4}{1991}\right)=\frac{1}{16}\cdot f\left(\frac{1458}{1991}\right).\] Como $\frac{1458}{1991}\not\in[\frac{1}{3},\frac{2}{3}]$, tomamos el número complementario para aplicar la tercera regla: \[f\left(\frac{1458}{1991}\right)=1-f\left(1-\frac{1458}{1991}\right)=1-f\left(\frac{533}{1991}\right).\] Volvemos a multiplicar por la mayor potencia de $3$: \[f\left(\frac{533}{1991}\right)=\frac{1}{2}\cdot f\left(\frac{3\cdot 533}{1991}\right)=\frac{1}{2}\cdot f\left(\frac{1599}{1991}\right).\] Como $\frac{1599}{1991}\not\in[\frac{1}{3},\frac{2}{3}]$, repetimos de nuevo el proceso: \[f\left(\frac{1599}{1991}\right)=1-f\left(1-\frac{1599}{1991}\right)=1-f\left(\frac{392}{1991}\right)=1-\frac{1}{2}\cdot f\left(\frac{1176}{1991}\right)=\frac{3}{4},\] ya que (ahora sí) $\frac{1176}{1991}\in[\frac{1}{3},\frac{2}{3}]$. Podemos entonces volver atrás y calcular $f(\frac{533}{1991})=\frac{3}{8}$ y $f(\frac{1458}{1991})=\frac{5}{8}$ y finalmente deducimos que \[f\left(\frac{18}{1991}\right)=\frac{5}{128}.\]
Nota. La función $f$ es la que se conoce como función escalera de Cantor. Una forma de calcular $f(x)$ es expresar $x$ como número decimal en base $3$ hasta llegar al primer decimal igual a $1$, cambiarlo por un $2$ y eliminar todos los que están a su derecha. Ahora todos los decimales son $0$ o $2$, cambiamos los ceros por unos y leemos el número en base $2$.
El procedimiento que se sigue en la solución de multiplicar por la mayor potencia de $3$ sin salirnos del intervalo y luego tomar complementarios, puede probarse que nos lleva a la solución siempre que acabe apareciendo un $1$ en la representación en base $3$ y hace que para tales números $x$, el valor de $f(x)$ sea racional. Los números para los que esto no se aplica son los que se escriben únicamente con $0$ y $2$ en base $3$, números que forman (una homotecia de razón $2$) del conjunto de Cantor (que son los números $x\in[0,1]$ que se escriben únicamente con $0$ y $1$ en base $3$).
Informar de error en enunciado Informar de procedencia del problema
Sesión 2 — 25 de septiembre de 1991
Informar de error en enunciado Informar de procedencia del problema
- Determinar cuántos elementos de $\{1,2,...,100\}$ son valores de $P$.
- Probar que el producto de valores de $P$ es un valor de $P$.
Por inspección directa, los números menores o iguales que 100 que son suma de dos cuadrados son: 1, 2, 4, 5, 8, 9, 10, 13, 16, 17, 18, 20, 25, 26, 29, 32, 34, 36, 37, 40, 41, 45, 49, 50, 52, 53, 58, 61, 64, 65, 68, 72, 73, 74, 80, 81, 82, 85, 89, 90, 97, 98, 100. Estos hacen un total de 43 valores de $P$ entre 1 y 100, lo que responde al apartado (a).
Para responder al apartado (b), veamos ahora que el producto de dos números que se expresan como suma de dos cuadrados vuelve a ser suma de dos cuadrados, pero esto es consecuencia de la siguiente identidad, válida para cualesquiera números $a$, $b$, $c$ y $d$ no necesariamente enteros: \[(a^2+b^2)(c^2+d^2)=(ac+bd)^2+(ad-bc)^2.\]
Informar de error en enunciado Informar de procedencia del problema
- Se determina el punto $X$ tal que $M$ es el punto medio de $XH$.
- Se traza la circunferencia de diámetro $XN$.
- Se ubica el vértice $A$ en la intersección de dicha circunferencia con la perpendicular a $MN$ que pasa por $H$.
- Se determinan los puntos $B$ y $C$ de forma que $M$ es el punto medio de $AB$ y $N$ es el punto medio de $AN$.
Ahora bien, puede ocurrir que la intersección de la recta y la circunferencia sea vacía, tenga un único punto o tenga dos puntos. Por el argumento previo, esto se corresponderá con que haya 0, 1 o 2 soluciones al problema. Se muestra en la figura un ejemplo en el que hay dos soluciones $A_1B_1C_1$ (en azul) y $A_2B_2C_2$ (en naranja).
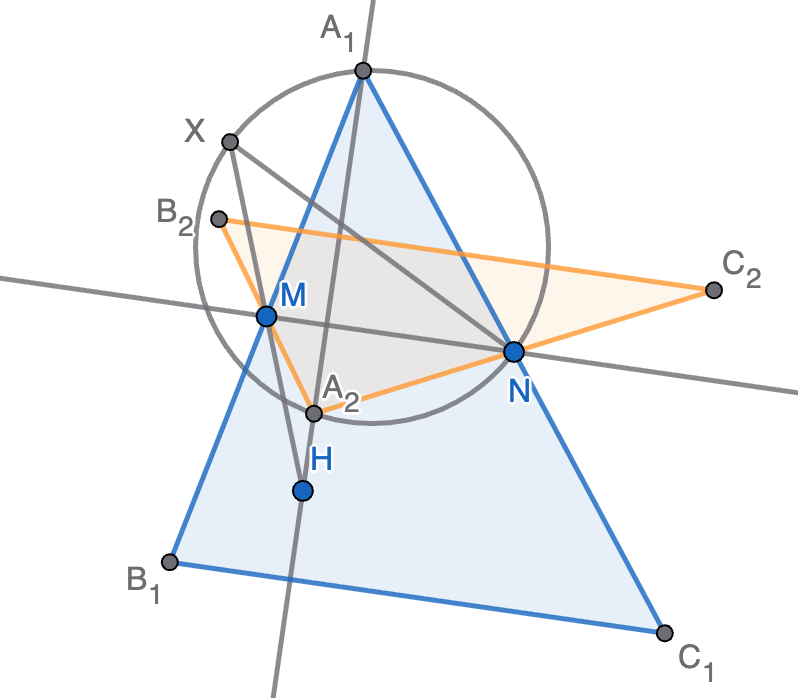
Nota. Sería interesante (como nuevo ejercicio), hallar condiciones sencillas sobre $M$, $N$ y $H$ para que exista solución.
Informar de error en enunciado Informar de procedencia del problema