Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
VII Olimpiada Iberoamericana de Matemáticas — 1992
Sesión 1 — 22 de septiembre de 1992
Informar de error en enunciado Informar de procedencia del problema
- Cada función $f_i(x)=\frac{a_i}{x+a_i}$ está definida en $\mathbb{R}-\{-a_i\}$ y es decreciente en todo su dominio, lo que nos dice que la función $f(x)=\sum_{i=1}^n f_i(x)$ está definida en $\mathbb{R}-\{-a_1,\ldots,-a_n\}$ y es continua y decreciente en todo su dominio.
- En cada punto de la forma $-a_i$, el límite de $f(x)$ por la derecha es $+\infty$ y por la izquierda $-\infty$, lo que nos dice que:
- Existe un único punto $x_1\gt-a_1$ tal que $f(x_1)=1$.
- Si $2\leq i\leq n$, existe un único punto $x_i\in(-a_i,-a_{i-1})$ tal que $f(x_i)=1$.
- $f(x)\lt 0$ para todo $x\lt-a_n$.
De todo esto deducimos que existen exactamente $n$ puntos $x_n\lt\cdots\lt x_2\lt x_1$ en los que la función toma el valor $1$. Además, los intervalos en que $f(x)\gt 1$ son los de la forma $(-a_i,x_i)$ para $1\leq i\leq n$, que tienen longitud $x_i+a_i$. Por tanto, la suma de longitudes buscada es \[S=x_1+x_2+\ldots+x_n+a_1+a_2+\ldots+a_n.\]
Volviendo a la expresión de la función, podemos poner denominador común para transformar la ecuación $f(x)=1$ en la ecuación polinómica de grado $n$ siguiente: \begin{eqnarray*} (x+a_1)\cdots(x+a_n)&-&a_1(x+a_2)\cdots(x+a_n)\\ &-&a_2(x+a_1)(x+a_3)\cdots(x+a_n)-\ldots-a_n(x+a_1)\cdots(x+a_{n-1})=0. \end{eqnarray*} Esto cuadra con la afirmación anterior de que existen exactamente $n$ valores de $x$ para los que $f(x)=1$, pero ahora sabemos que son las raíces de este polinomio. Es fácil ver que este polinomio tiene coeficiente de $x^n$ igual a $1$ y coeficiente de $x^{n-1}$ igual a $0$, luego las relaciones de Cardano-Vieta nos dicen que la suma de sus raíces es $x_1+\ldots+x_n=0$. Deducimos finalmente que la suma de las longitudes de los intervalos que nos piden es $S=a_1+a_2+\ldots+a_n$.
Informar de error en enunciado Informar de procedencia del problema
- Demostrar que para cada punto $P$ de $\Gamma$, la suma de los cuadrados de sus distancias a los vértices $A$, $B$ y $C$ es $5$.
- Demostrar que para todo punto $P$ de $\Gamma$ es posible construir un triángulo cuyos lados tienen las longitudes de los segmentos $AP$, $BP$ y $CP$ y cuya área es $\frac{\sqrt{3}}{4}$.
Que se puede formar un triángulo con los segmentos $AP,BP,CP$ es cierto para cualquier punto interior al triángulo. Observemos que podemos prolongar $AP$ hasta llegar a un punto $D$ del lado $BC$. Con lo que $AP\leq AD\leq BC\leq BP+PC$, donde hemos usado que la longitud de $AD$ es menor que la longitud de un lado y la desigualdad triangular. Se razona de la misma forma que $BP\leq AP+CP$ y que $CP\leq AP+BP$.
Para calcular el área del triángulo, llamemos $a=AP$, $b=BP$ y $c=CP$ por comodidad. La fórmula de Herón nos dice que \begin{align*} 16S^2&=(a+b+c)(-a+b+c)(a-b+c)(a+b-c)\\ &=((b+c)^2-a^2)((b-c)^2-a^2)\\ &=-a^4+2 a^2 b^2+2 a^2 c^2-b^4+2 b^2 c^2-c^4\\ &=4(a^2b^2+b^2c^2+c^2a^2)-(a^2+b^2+c^2)^2. \end{align*} Hemos probado que $a^2+b^2+c^2=5$ y también es fácil comprobar que \[a^2b^2+b^2c^2+c^2a^2=3(x^2+y^2)^2+4(x^2+y^2)+\tfrac{16}{3}=7,\] lo que nos lleva a que $16S^2=4\cdot 7-25=3$ y, por tanto, $S=\frac{\sqrt{3}}{4}$.
Informar de error en enunciado Informar de procedencia del problema
Sesión 2 — 23 de septiembre de 1992
- $a_0=0$ y $b_0=8$,
- $a_{n+2}=2a_{n+1}-a_n+2$ y $b_{n+2}=2b_{n+1}-b_n$,
- $a_n^2+b_n^2$ es un cuadrado perfecto para todo $n$.
- Una solución es $a_n=n^2+4n$ y $b_n=4n+8$ para todo $n\in\mathbb N$, que nos da $(a_{1992},b_{1992})=(3976032,7976)$.
- La otra solución es $a_n=n^2-4n$ y $b_n=-4n+8$ para todo $n\in\mathbb N$, que nos da $(a_{1992},b_{1992})=(3960096,-7960)$.
Nota. Dada una sucesión definida por una recurrencia $x_{n+2}=a x_{n+1}+bx_n$, esta tiene polinomio característico $x^2-ax-b$. Si este polinomio tiene dos raíces distintas $\lambda$ y $\mu$, entonces la sucesión es de la forma $x_n=r\lambda^n+s\mu^n$ para ciertas constantes $r$ y $s$. Si el polinomio tiene una raíz doble $\lambda$, entonces las soluciones son de la forma $x_n=c\lambda^n+dn\lambda^n$ para ciertas constantes $c$ y $d$. Las constantes se determinan imponiendo la condición inicial.
En el caso de la recursión no homogénea $x_{n+2}=a x_{n+1}+bx_n+f(n)$, se ha de comenzar encontrando una solución particular. En el caso de que $f(n)$ sea un polinomio, la solución particular es un polinomio (por eso hemos probado con polinomios de un grado superior en este problema). Una vez obtenida la solución particular, la solución general es la suma de la solución particular con todas las soluciones de la ecuación homogénea asociada (para $f(n)=0$).
Informar de error en enunciado Informar de procedencia del problema
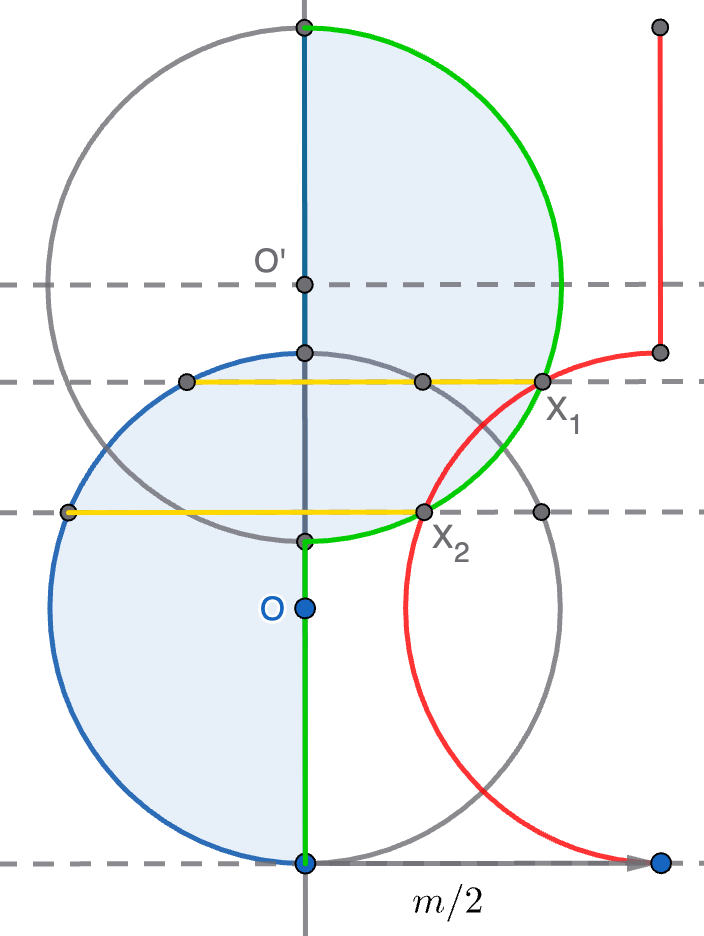
Consideremos entonces el eje de simetría vertical común a ambas circunferencias y nos quedamos con la semicircunferencia $S$ de $\Gamma$ a la derecha del eje y con la semicircunferencia $S'$ de $\Gamma'$ a la derecha del eje, delimitando ambas la región sombreada de la figura. Como nos hemos quedado con la mitad de cada circunferencia, ahora queremos ver qué recta horizontal corta a la zona sombreada en una longitud $\frac{m}{2}$. Para ello, movemos la figura $\frac{m}{2}$ a la derecha y vemos dónde corta el borde izquierdo trasladado (en rojo en la figura) al borde derecho original (en verde). Cada punto $X$ en la intersección nos da una posible solución que viene dada por la recta horizontal que pasa por $X$. En la figura se ha puesto un ejemplo en el que hay dos soluciones $X_1$ y $X_2$ que producen sendos segmentos de longitud $\frac{m}{2}$, indicados en amarillo.
Informar de error en enunciado Informar de procedencia del problema
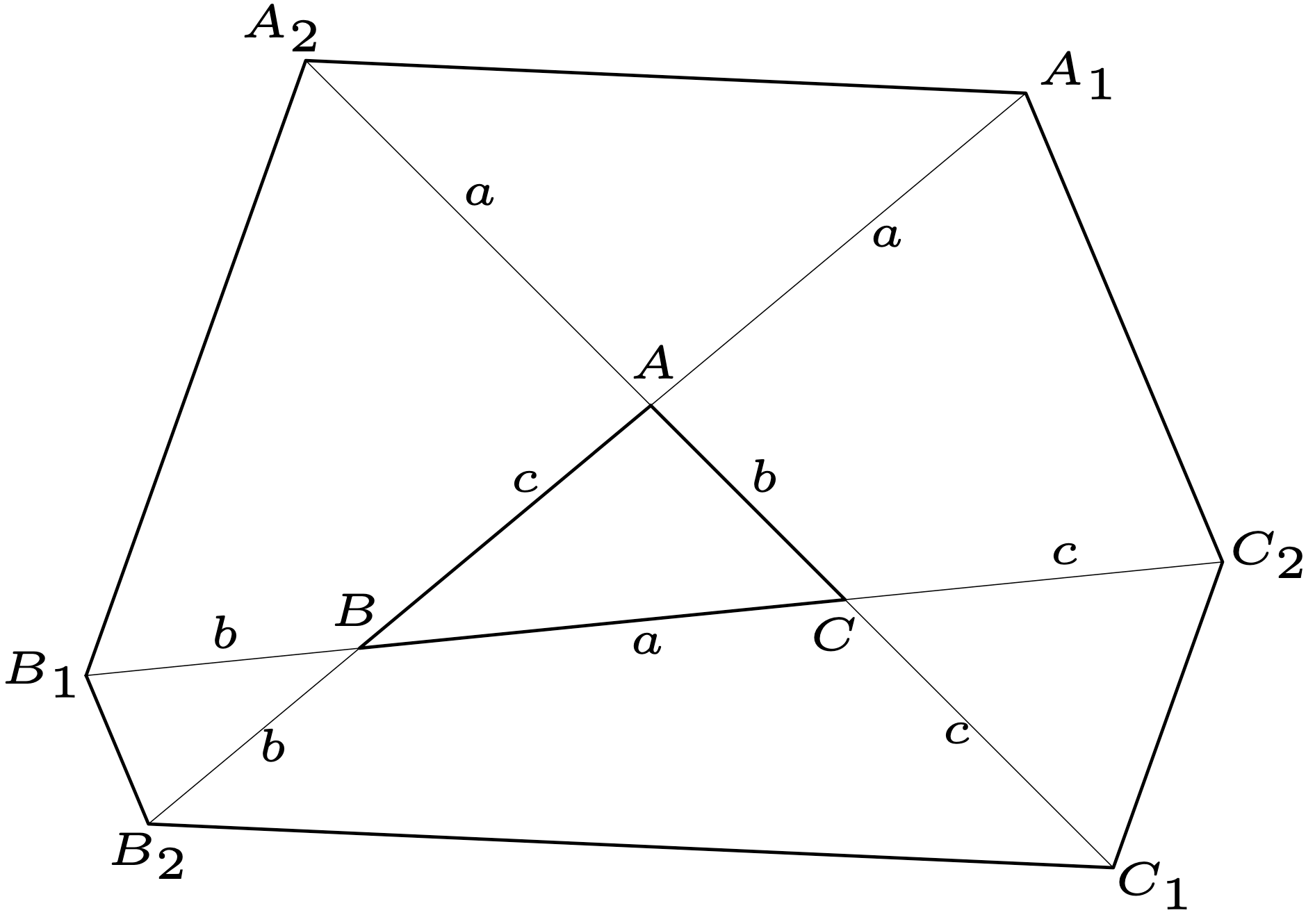
Nota. La igualdad se alcanza si, y sólo si, el triángulo es equilátero.
Informar de error en enunciado Informar de procedencia del problema