Olimpiadas de Matemáticas
Página de preparación y problemas

Solución. Supongamos en primer lugar que $x_i$ e $x_{i+1}$ tienen el mismo número de cifras y supongamos que es impar, pongamos $2n+1$, con $n\geq 1$ (el caso de números de una cifra nos da diferencia $x_{i+1}-x_i=1$, que no es primo). Entonces, podemos escribir \[x_i=a_1a_2\ldots a_na_{n+1}a_n\ldots a_2a_1.\] Por lo tanto, $x_i$ está determinado por el número $m=a_1a_2\ldots a_na_{n+1}$ formado por las $n+1$ cifras más significativas. El siguiente número capicúa $x_{i+1}$ tiene una estructura similar pero tiene número asociado $m+1$. Si se cumple que alguno de los dígitos $a_2,\ldots,a_{n+1}$ es distinto de $9$, entonces $m+1$ y $m$ tienen el mismo dígito inicial $a_1$ (que también es el dígito de las unidades de $x_{i+1}$ y $x_i$), por lo que $x_{i+1}-x_i$ es múltiplo de $10$ y no es primo. Supongamos ahora que a_2=\ldots=a_{n+1}=9$, luego $x_i=a_199\ldots99a_1$ y $x_{i+1}=(a_1+1)00\ldots00(a_1+1)$. En consecuencia, en este caso tenemos que $x_{i+1}-x_i=11$, que sí es primo.

Si ahora $x_i$ y $x_{i+1}$ tienen el mismo número de cifras y este número es par $2n$, con $n\geq 2$ (el caso $n=2$ nos da claramente el primo $11$), el razonamiento es similar tomando $m=a_1a_2\ldots a_n$ el número formado por las $n$ cifras más significativas.

Finalmente, si $x_i$ y $x_{i+1}$ tienen distinto número de cifras, entonces $x_i=999\ldots 99$ y $x_{i+1}=1000\ldots 01$, que tienen diferencia $2$ unidades. Deducimos así que los únicos primos que se pueden expresar de esta forma son $2$ y $11$.

Solución. Sean $A$ y $B$ los dos vértices más alejados entre sí del polígono y consideramos los dos vértices $C$ y $D$ más alejados de la recta $AB$ en sendos semiespacios definidos por $AB$. Trazamos por $A$ y $B$ perpendiculares $r_A$ y $r_B$ a $AB$ y por $C$ y $D$ paralelas $r_C$ y $r_D$ a $AB$. Estas cuatro rectas $r_A,r_B,r_C,r_D$ determinan un rectángulo $R$. Vamos a ver que $R$ (que es, en particular, paralelogramo) contiene al polígono y que tiene área menor o igual que $2$.

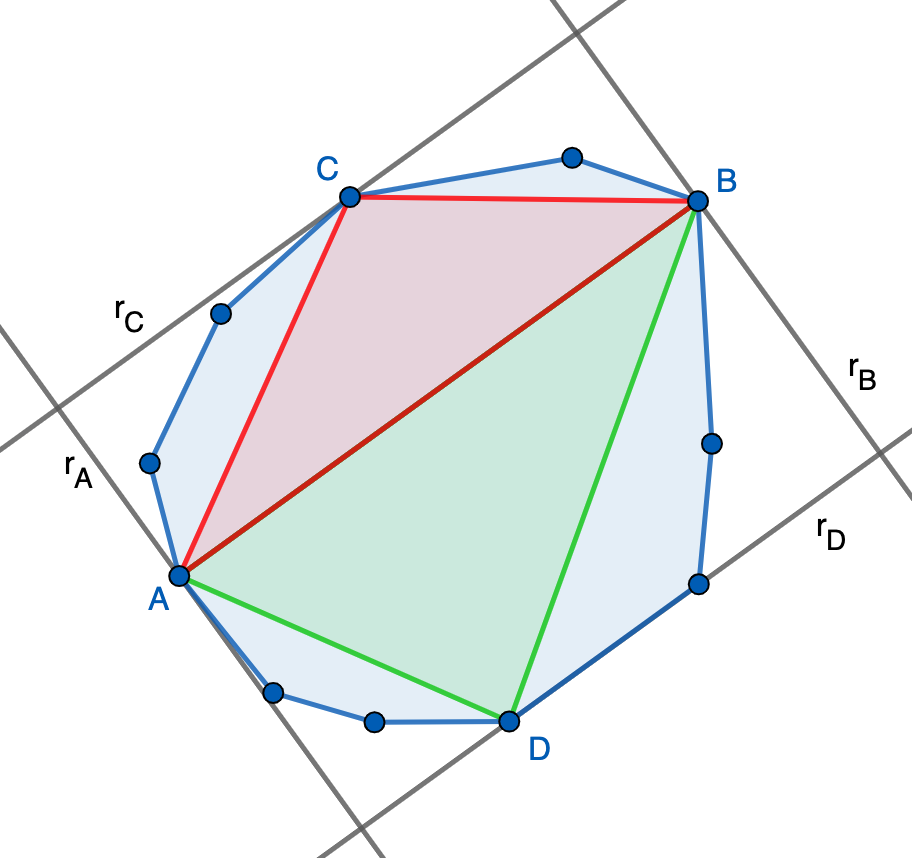
• En primer lugar, tenemos que ningún vértice se puede salir de la banda determinada por $r_A$ y $r_B$ ya que en tal caso dicho vértice tendría distancia con $A$ o con $B$ mayor que $AB$ (¿por qué?), contradiciendo que $AB$ es el segmento entre vértices de longitud máxima. Por otro lado, ningún vértice se puede salir de la banda determinada por $r_C$ y $r_D$ ya que en tal caso dicho vértice distaría de $AB$ más que $C$ o $D$, contradiciendo que estos son los puntos más alejados. Por tanto, todos los vértices del polígono están en $R$ y, por convexidad, todo el polígono debe estar en $R$.
• Finalmente, veamos que $\text{área}(R)\leq 2$. Para ello, observamos que los triángulos $ACB$ y $ADB$ están contenidos en el polígono (de nuevo, por convexidad), de donde \[1=\text{área}(\text{polígono})\geq\text{área}(ACB)+\text{área}(ADB)=\tfrac{1}{2}\text{área}(R).\]

Esto termina la demostración. Es importante observar que uno de los dos puntos $C$ o $D$ podría no estar definido porque no haya vértices a un lado de la recta $AB$. En tal caso, se razona de forma similar usando que $r_C=AB$ o $r_D=AB$.

Solución. Haciendo $x=y=1$, obtenemos $f(f(1))=f(1)$ pero $f$ es inyectiva al tratarse de una función estrictamente creciente, luego $f(1)=1$. Haciendo $y=f(x)$ en la ecuación, tenemos que \[f(f(x)^2)=x^2f(xf(x))=x^4f(x^2).\] Haciendo ahora $y=1$ en la ecuación y cambiando $x$ por $x^2$, tenemos que $f(f(x^2))=x^4f(x^2)$, luego deducimos que $f(f(x)^2)=f(f(x^2))$ y de la inyectividad obtenemos que $f(x)^2=f(x^2)$. Veamos que la única solución posible es $f(x)=x^2$ para todo $x$, para lo que razonaremos por reducción al absurdo, distinguiendo dos casos:

• Si $f(x)\gt x^2$ para algún $x$, entonces podemos usar la monotonía para llegar a que \[x^2f(x)=f(f(x))\gt f(x^2)=f(x)^2,\] luego $f(x)\lt x^2$ (ya que $f(x)\neq 0$)), que es obviamente un absurdo.
• Si $f(x)\lt x^2$ para algún $x$, podemos razonar de forma similar para obtener que \[x^2f(x)=f(f(x))\lt f(x^2)=f(x)^2,\] luego $f(x)\gt x^2$ y también tenemos una contradicción.

Nota. ¿Qué ocurre si exigimos que $f:\mathbb{Z}\to\mathbb{Z}$, $f:\mathbb{Q}\to\mathbb{Q}$ o $f:\mathbb{R}\to\mathbb{R}$ con las mismas condiciones?

Solución. Llamemos $T$ al punto de tangencia de $MN$ con la circunferencia inscrita y $\ell$ al lado del triángulo. Observemos que la longitud de $MT$ es igual a la del segmento que une $M$ con el punto medio del lado $AB$ por la propiedad de tangencia. Por tanto, $AM+MT=\frac{\ell}{2}$ y, de la misma forma, $AN+NT=\frac{\ell}{2}$, con lo que el perímetro del triángulo $AMN$ es exactamente $\ell$. Así, podemos escribir \[\frac{AM}{MB}+\frac{AN}{NC}=\frac{AM}{MN+AN}+\frac{AN}{MN+AM}=\frac{AM^2+AN^2+MN(AN+AM)}{MN^2+MN(AN+AM)+AM\cdot AN}.\] Por lo tanto, quisiéramos demostrar que $AM^2+AN^2=MN^2+AM\cdot AN$, pero esto se deduce de forma fácil del teorema del coseno aplicado al triángulo $AMN$ teniendo en cuenta que $\angle MAN=60^\circ$.