Olimpiadas de Matemáticas
Página de preparación y problemas

Solución. Que el número $n$ sea sensato equivale a que \[n=a(1+r+r^2+\ldots+r^k)\] para ciertos $a,r\in\mathbb{N}$ tales que $1\lt r\lt n-1$ y $1\leq a\leq r-1$. El caso de $1994=2\cdot 997$ es obvio ya que basta tomar $a=2$, $r=996$ y $k=1$, lo que nos da la representación $1994=22_{(996)}$.

Como $1993$ es primo, no vale el truco anterior y tenemos que necesariamente $a=1$. Por tanto, $1993$ será sensato cuando podamos encontrar $r,k\geq 2$ tales que \[1993=1+r+\ldots+r^k.\] Esta ecuación nos dice además que $r$ debe ser un divisor de $1992=2^3\cdot 3\cdot 81$. No obstante, $r$ no puede ser múltiplo de $81$ ya que $81^2\gt 1993$, lo que nos deja sólo las posibilidades $r\in\{2,3,4,6,8,12,24\}$. En realidad, se pueden probar una a una sin perder demasiado tiempo, pero una opción sin tanto cálculo es observar que \[1993=1+r+\ldots+r^k=\frac{r^{k+1}-1}{r-1}\ \Leftrightarrow\ 1+1993(r-1)=r^{k+1},\] luego sólo tenemos que calcular $1+1993(r-1)$ y ver si es potencia de $r$ o no:

• Para $r=2$, tenemos que $1+1993(r-1)=1994=2\cdot 997$ no es potencia de $2$.
• Para $r=3$, tenemos que $1+1993(r-1)=3987=9\cdot 443$ no es potencia de $3$.
• Para $r=4$, tenemos que $1+1993(r-1)=5980$ es múltiplo de $5$ y no es potencia de $4$.
• Para $r=6$, tenemos que $1+1993(r-1)=9966$ es múltiplo de $11$ y no es potencia de $6$.
• Para $r=8$, tenemos que $1+1993(r-1)=13952=2^7\cdot 109$ no es potencia de $8$
• Para $r=12$, tenemos que $1+1993(r-1)=21924$ es múltiplo de $7$ y no es potencia de $12$.
• Para $r=24$, tenemos que $1+1993(r-1)=45840$ es múltiplo de $5$ y no es potencia de $24$.

Concluimos que $1993$ no es sensato.

Solución. Si $n$ es impar, podemos tocar todas las lámparas de la primera fila (o de culquier fila o columna) y las $n^2$ lámparas quedan encendidas. Es fácil ver que $n$ es realmente el mínimo número de toques ya que, si sólo tocáramos $n-1$ lámparas o menos, entonces habría al menos una fila y al menos una columna en la que no tocaríamos ninguna lámpara. La casilla intersección de esta fila y columna quedaría apagada.

Por otro lado, si $n$ es par y tocamos las $n^2$ lámparas, también quedarán todas encendidas ya que a cada lámpara le afectan $2n-1$ cambios de estado (en realidad, esto también funciona para $n$ impar pero no es óptimo, como acabamos de ver). Vamos a demostrar que, si no tocamos todas las lámparas, entonces habrá alguna que quede apagada, lo que probará que $n^2$ es óptimo en el caso $n$ par y habremos terminado.

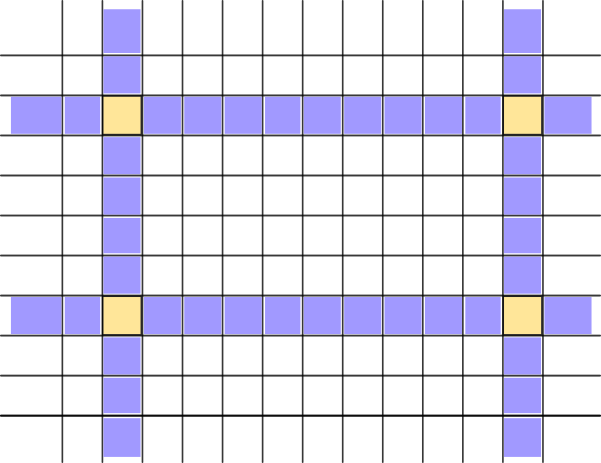
Llamaremos $c_{ij}$ a la casilla de la fila $i$ y la columna $j$ y le asignaremos un valor $0$ o $1$ dependiendo de si se ha tocado o no (no tiene sentido tocarla más de una vez). Comenzaremos probando que en cualesquiera cuatro casillas $c_{ij},c_{ik},c_{hj},c_{hk}$ que forman los vértices de un cuadrado (como las indicadas en naranja en la imagen) hay un número par de toques. Observamos en primer lugar que cada toque en casillas las filas $i$ y $h$ o de las columnas $j$ y $k$ distintas de los vértices del cuadrado (pintadas de morado) cambia exactamente a dos de los vértices naranjas. Como tocar uno de los vértices cambia el estado de tres de ellos, es inmediato que hay que pulsar un número par de vértices para que los cuatro queden encendidos.

Consideremos ahora dos columnas cualesquiera del tablero. El razonamiento anterior (aplicado a todas las casillas que sean vértices un cuadrado contenido en esas dos columnas) nos dice que o bien las dos columnas son iguales (tienen los mismos ceros y unos en la misma posición) o bien son opuestas (una tiene ceros donde la otra tiene unos y viceversa). Esta última situación no es posible si $n$ es par ya que, si nos fijamos en las dos casillas de la primera fila, tendrán paridades distintas de toques provenientes de su columna, pero el mismo número de toques provenientes de su fila, lo que nos lleva a que ambas no pueden estar encendidas. Hemos probado así que todas las columnas son iguales y el mismo razonamiento puede aplicarse a las filas, luego necesariamente hemos tenido que tocar todas las lámparas.

Solución. Si tenemos subconjuntos $A_1,A_2,\ldots,A_r$ de $k$ elementos cada uno, entonces el número de sumas distintas $x_1+x_2+\ldots+x_r$ con $x_1\in A_1$, $x_2\in A_2$, ..., $x_r\in A_r$ será como máximo $k^r$, ya que podemos elegir de entre $k$ elementos para cada $x_i$, pero podría haber sumas repetidas. Por lo tanto, deducimos que si todos los enteros $x$ tales que $0\leq x\leq n-1$ se pueden expresar de esta forma, se tendrá que cumplir necesariamente que $k^r\geq n$ o, equivalentemente, $k\geq n^{1/r}$. Como $k$ tiene que ser un número entero, obtenemos que $k\geq\lceil n^{1/r}\rceil$. Si demostramos que se pueden construir los subconjuntos con $k=\lceil n^{1/r}\rceil$ elementos, este será el mínimo de $k$ que nos piden y habremos terminado.

Para $k=\lceil n^{1/r}\rceil$ construimos los $r$ subconjuntos \[A_m=\{a\,k^{m-1}:0\leq a\in\leq k-1\},\qquad\text{para } 1\leq m\leq r-1.\] Cada $A_m$ tiene $k$ elementos, exactamente los números que en base $k$ tienen $m$ cifras siendo las $m-1$ menos significativas todas cero (observemos que $0\in A_m$ para todo $m$). Todo número entre $0$ y $k^r-1$ se expresa de forma única como suma de un elemento de cada subconjunto (de $A_1$ tomamos el que tiene la cifra de sus unidades en base $k$, de $A_2$ el que tiene la cifra de sus decenas, y así sucesivamente). Ahora bien, el número máximo que puede expresarse de esta forma es $k^r-1=\lceil n^{1/r}\rceil^r-1\geq (n^{1/r})^r-1=n-1$, lo que concluye la demostración.

Solución. Las primeras $2^{12}-2=4094$ sumas las emplearemos en obtener los números desde el $2$ hasta el $2^{12}-1$ sin más que sumar $1$ consigo mismo repetidamente. En base $2$ esto nos da todos los números de $11$ cifras y también el $2^{12}$, que es un uno seguido de once ceros. Veamos cómo usar esto para hallar cualquier número $n$ de $999999$ cifras en base $2$, cifras que se pueden agrupar en $90909$ grupos de once dígitos consecutivos formando números de once cifras $S_1,S_2,\ldots,S_{90909}$, siendo $S_1$ las once cifras más significativas

Como $S_1\leq 4095$, este número se encuentra entre los calculados. Ahora lo sumamos consigo mismo para obtener $2S_1$ y este resultado lo sumamos consigo mismo para obtener $4S_1$ y así sucesivamente hasta obtener $2^{11}S_1$, que es el número $S_1$ seguido de $11$ ceros. Ahora sumamos al resultado $S_2$ y ya tenemos el número $2^{11}S_1+S_2$, que contiene las veintidós cifras más significativas de $n$. Lo sumamos consigo mismo de forma que en otros once pasos obtenemos $2^{22}S_1+2^{11}S_2$ y le sumamos $S_3$. Podemos repetir este proceso para conseguir todas las cifras de $n$. Por cada grupo de once cifras que añadimos, hemos necesitado $12$ sumas (once para multiplicar por $2^{11}$ y una para añadir once nuevos dígitos), lo que hace un total de $4095+12\cdot 90908=1094991\lt 1100000$.

Queda el caso de que $n=2^{1000000}$, pero este número se obtiene con solo $1000000$ sumas sin más que sumar $1$ consigo mismo y luego $2$ consigo mismo, luego $4$ consigo mismo, y así sucesivamente.

Nota. Esta solución funciona haciendo grupos de $11$ (como hemos hecho), de $12$ (se obtiene un máximo de $1091520$ sumas) o $13$ dígitos ($1093291$ sumas). Con grupos de más de $13$ dígitos o de menos de $11$, necesitaríamos en general más de $1100000$ sumas mediante este método.