Olimpiadas de Matemáticas
Página de preparación y problemas

Solución. Tenemos que el $55,\!5555\ldots\%$ el $27,\!1818\ldots\%$ y el $37\%$ representan fracciones irreducibles $\frac{5}{9}$, $\frac{299}{1100}$ y $\frac{37}{100}$ del total. Por lo tanto, el número de afiliados tiene que ser múltiplo de $\operatorname{mcm}(9,1100,100)=9900$. El único múltiplo positivo de $9900$ menor o igual que $15000$ es el propio $9900$, luego sí es posible calcular el número de afiliados.

Observemos que esto implica que hay $2691$ mujeres y $5500$ mayores de $30$ años y que $3663$ llevaban un libro de matemáticas.

Solución. Pongamos coordenadas de forma que $A=(0,0)$, $B=(c,0)$ y $C=(0,b)$. El teorema de la bisectriz nos dice que los segmentos $AM$ y $MB$ son proporcionales a $b$ y $a$, respectivamente; como suman $c$, tiene que ser $AM=\frac{bc}{a+b}$ y $MB=\frac{ac}{a+b}$. De la misma manera, se tiene que $AN=\frac{bc}{a+c}$ y $NC=\frac{ba}{a+c}$, luego tenemos las coordenadas $M=(\frac{bc}{a+b},0)$ y $N=(0,\frac{bc}{a+c})$. Por lo tanto, la recta $MN$ tiene ecuación $(a+b)x+(a+c)y=bc$ y, por su parte, la recta $AD$ tiene ecuación $cx-by=0$ (ya que pasa por $(0,0)$ y el vector $(c,-b)$ es un vector normal). La intersección de estas dos rectas es el punto \[P=\left(\frac{b^2c}{b^2+c^2+ab+ac},\frac{bc^2}{b^2+c^2+ab+ac}\right)=\left(\frac{b^2c}{a(a+b+c)},\frac{bc^2}{a(a+b+c)}\right),\] donde hemos simplificado usando que $a^2=b^2+c^2$ por el teorema de Pitágoras. La distancia de este punto al origen es \[AD=\sqrt{\left(\frac{b^2c}{a(a+b+c)}\right)^2+\left(\frac{bc^2}{a(a+b+c)}\right)^2}=\sqrt{\frac{b^2c^2(b^2+c^2)}{a^2(a+b+c)^2}}=\frac{bc}{a+b+c},\] donde hemos usado de nuevo el teorema de Pitágoras para simplificar. Esto último es igual al radio de la circunferencia inscrita (ver la nota), lo que concluye la demostración.

Nota. En un triángulo rectángulo de hipotenusa $a$ y catetos $b$ y $c$, el área se puede calcular como $\frac{1}{2}bc$, ya que los catetos hacen de base y altura, y también como $S=rp=\frac{1}{2}(a+b+c)r$. Igualando ambas expresiones, obtenemos que $r=\frac{bc}{a+b+c}$.

Solución. Consideramos una teselación del plano infinito por piezas de tamaño $2\times 1$ y $1\times 2$ formando escaleras infinitas, como se muestra en la figura. Cada vez que A coloca en una casilla, la estrategia de B es colocar en la otra casilla de la misma pieza. De esta forma, A nunca puede conseguir 5 en fila porque cualquier rectángulo $5\times 1$ o $1\times 5$ contiene completamente a alguna de las piezas $2\times 1$ o $1\times 2$, respectivamente.

Solución. Como $\operatorname{sen}(x)\lt x$ para todo $x\in(0,\frac{\pi}{2})$ y el coseno es una función decreciente, tenemos la cadena de desigualdades \[\operatorname{sen}(\cos(x))\lt\cos(x)\lt\cos(\operatorname{sen}(x)).\] Por tanto, los puntos en que estas funciones cortan a la recta $y=x$ estarán en el mismo orden que las funciones, es decir, $b\lt a\lt c$ (en la imagen puede verse una representación gráfica de las tres funciones y la recta).

Solución. Como $2^{11}=2048\gt 1995$, está claro que $n=11$ es válido. Explícitamente, \[\frac{15}{17}-\frac{k}{2^{11}}=\frac{30720-17k}{17\cdot 2^{11}}=\frac{17(1087-k)+1}{17\cdot 2^{11}}=\frac{1}{17\cdot 2^{11}}\lt\frac{1}{1995}\] para $k=1807$. Vamos a ver que no es posible obtener un valor de $k$ para $n=10$ y, por tanto, tampoco será posible encontrarlo para $n\lt 10$ ya que cualquier número de la forma $\frac{k}{2^n}$ con $n\lt 10$ también es de la forma $\frac{k}{2^{10}}$. Repitiendo el proceso anterior que hicimos para $n=11$, tenemos que \[\frac{15}{17}-\frac{k}{2^{10}}=\frac{15360-17k}{17\cdot 2^{10}}=\frac{17(903-k)+9}{17\cdot 2^{10}}=\frac{903-k}{2^{10}}+\frac{9}{17\cdot 2^{10}}.\] Entonces, el valor de $k$ que minimiza la diferencia es $k=903$, pero para este valor dicha diferencia es $\frac{9}{17\cdot 2^{10}}\gt\frac{1}{1995}$.

Solución. Dado que toda la figura es de revolución, podemos simplificar el razonamiento pensando en un objeto bidimensional que debe ser rotado respecto de un eje. Denotamos por $O_n$ el centro de la circunferencia $n$-ésima, por $T_n$ el punto de tangencia con una de las directrices del cono y por $P_{n+1}$ el punto de tangencia con la circunferencia $(n+1)$-ésima, como se indica en la figura. Dado que los radios que pasan por los puntos de tangencia son perpendiculares a la recta de tangencia, se tiene que $O_nT_nT_{n+1}O_{n+1}$ es un trapecio con ángulos rectos en $T_n$ y $T_{n+1}$, ángulo de $60^\circ$ en $O_{n+1}$. Por lo tanto, se verifica que \[\frac{1}{2}=\cos(60)=\frac{r_{n+1}-r_n}{r_{n+1}+r_n}\ \Longleftrightarrow\ r_{n+1}=3r_n.\] En otras palabras, cada radio es el triple del anterior, luego se tiene que $r_n=3^{n-1}r_1$ y hemos respondido al primer apartado.

En cuanto al volumen, observamos que éste se puede calcular como el del cono truncado que surge al revolucionar la región naranja al que hay que quitarle dos casquetes esféricos, uno de la esfera $n$-ésima y otro de la esfera $(n+1)$-ésima. Vamos por partes:

• En el triángulo $OT_nO_n$ podemos calcular $\tan(30)=\frac{r_n}{OT_n}$, de donde $OT_n=r_n\sqrt{3}$. Ahora en el triángulo $OA_nT_n$ podemos calcular $A_nT_n=OT_n\operatorname{sen}(30)=\frac{\sqrt{3}}{2}r_n$ y $OA_n=OT_n\cos(30)=\frac{3}{2}r_n$. Por tanto, el cono de revolución del triángulo $OA_nT_n$ tiene volumen $V_n=\frac{1}{3}\pi(A_nT_n)^2(OA_n)=\frac{3}{8}\pi r_n^3$. El volumen de revolución del trapecio naranja será $V_{n+1}-V_n=\frac{3}{8}\pi(r_{n+1}^3-r_n^3)=\frac{39}{4}\pi r_n^3$.
• Como el triángulo $O_{n+1}P_{n+1}T_{n+1}$ es equilátero, $A_{n+1}$ es el punto medio de $P_{n+1}O_{n+1}$. Esto nos dice que buscamos el volumen de un casquete de la esfera $(n+1)$-ésima de altura la mitad su radio. La fórmula para el volumen del casquete nos da $\frac{5}{24}\pi r_{n+1}^3=\frac{45}{8}\pi r_n^3$.
• El mismo casquete en la esfera $n$-ésima tiene volumen $\frac{5\pi}{24}r_n^3$, pero en este caso necesitamos el casquete complementario, cuyo volumen será $\frac{4}{3}\pi r_n^3-\frac{5}{24}\pi r_n^3=\frac{9}{8}\pi r_n^3$.

Con todo esto, el volumen que buscamos para el apartado (b) es \[\frac{39}{4}\pi r_n^3-\frac{45}{8}\pi r_n^3-\frac{9}{8}\pi r_n^3=3\pi r_n^3.\]

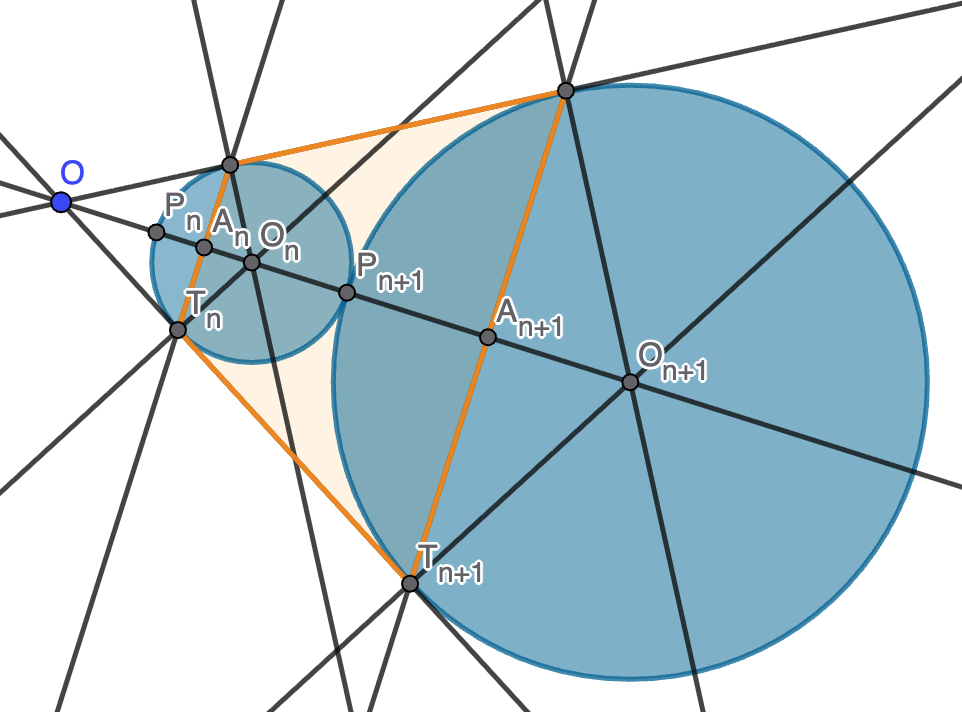
Nota. El volumen de un casquete esférico de altura $h$ en una esfera de radio $r$ es $\frac{\pi}{3}h^2(3r-h)$.

Solución. En un torneo hay $n-1$ partidos que se podemos suponer que se juegan en un orden preestablecido, es decir, que ya están colocados en el calendario, uno cada día, antes incluso de decidir qué jugadores se enfrentan en la primera eliminatoria. De esta forma, podemos numerar los encuentros del $1$ al $n-1$. Numeramos también los jugadores del $1$ al $n$ y denotamos por $p_{ij}^k$ la probabilidad de que se enfrenten el jugador $i$ y el jugador $j$ en el partido $k$-ésimo. Como los jugadores se emparejan aleatoriamente y son igualmente hábiles, tendremos que $p_{ij}^k$ es una constante $p$ que no depende de $i$ ni de $j$ ni de $k$. Por tanto, se tiene que \[\binom{n}{2}(n-1)p=\sum_{k=1}^{n-1}\sum_{i\lt j}p_{ij}^k=\sum_{k=1}^{n-1}1=n-1.\] De aquí deducimos que $p=\frac{2}{n(n-1)}$. Sin embargo, la probabilidad que nos piden no es que se enfrenten en un partido en concreto sino en cualquiera de ellos. Como no es posible enfrentarse más de una vez, el resultado que buscamos será el número de partidos multiplicado por la probabilidad de enfrentarse en uno de ellos, es decir, $(n-1)p=\frac{2}{n}$.

Solución. Los $8$ elementos forman un total de $\binom{8}{2}=\frac{8\cdot 7}{2}=28$ parejas de elementos. Ahora bien, un elemento dado no puede estar en cuatro o más subconjuntos ya que entonces habría dos de estos subconjuntos con otro elemento en común. Esto quiere decir que hay al menos $4$ de las $28$ parejas que no pertenece a ninguno de los subconjuntos, lo que hace un máximo de $24$ parejas que pueden estar en cada subconjunto. Como cada subconjunto tiene tres parejas de elementos, habrá un máximo de $8$ subconjuntos.

Será suficiente entonces encontrar ocho subconjuntos de tres elementos que cumplen la propiedad del enunciado, pero esto es ya sencillo tras probar un poco. Si el conjunto es $A=\{1,2,3,4,5,6,7,8\}$, entonces podemos tomar los subconjuntos $\{1,2,3\}$, $\{3,4,5\}$, $\{5,6,7\}$, $\{7,8,1\}$, $\{1,4,6\}$, $\{3,6,8\}$, $\{5,8,2\}$ y $\{7,2,4\}$. Cada uno de ellos corta a otros $6$ y lo hace en un único elemento.