Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
XXXIV Olimpiada Matemática Española (fase local) — 1998
Sesión 1 — 16 de enero de 1998 (tarde)
Nota. No es difícil terminar el razonamiento y ver que las soluciones al problema son \[(a,b)=\left(21\sqrt{3},5\sqrt{3}\right)\qquad\text{y}\qquad (a,b)=\left(-21\sqrt{3},-5\sqrt{3}\right).\]
Informar de error en enunciado Informar de procedencia del problema
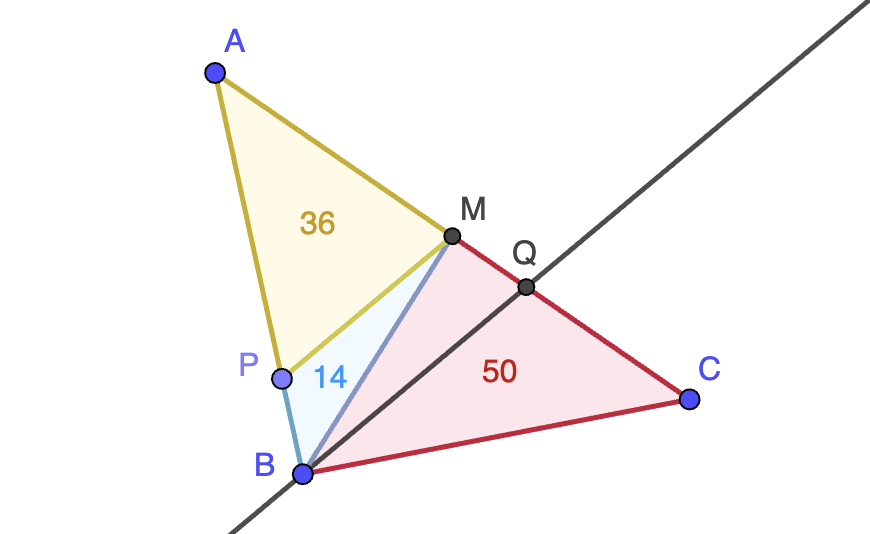
Por un lado, si existe tal punto en $OP$, esto quiere decir que existen $c,d\in\mathbb{N}$ y $0\lt\lambda\lt 1$ tales que $(c,d)=\lambda(a,b)$. En particular, $\lambda=\frac{c}{a}=\frac{d}{b}$ es un número racional. Supongamos que $\lambda=\frac{m}{n}$ como fracción irreducible, luego \[c=\frac{m}{n}a,\qquad d=\frac{m}{n}b,\] de forma que $n$ debe ser un divisor común a $a$ y $b$. Observemos que $n\gt 1$ ya que $0\lt \lambda\lt 1$, luego hemos probado que $a$ y $b$ no son primos entre sí. Recíprocamente, si $n\gt 1$ es un divisor común a $a$ y $b$, entonces el punto $(c,d)=(\frac{a}{n},\frac{b}{n})$ es un punto de coordenadas enteras en el segmento $OP$, lo que concluye la demostración.
Con esta información, el problema se traduce en ver cuántos números enteros $k$ entre $1$ y $1998$ son primos relativos con $1000$. Como $1000=2^3\cdot 5^3$, estamos buscando los valores de $k$ que no tienen factores primos $2$ ni $5$. De los $1998$ números considerados, hay $999$ múltiplos de $2$, $399$ múltiplos de $5$ y $199$ múltiplos de $10$ (¿sabrías contarlos rápidamente?). Por tanto, la cantidad de primos relativos con $1000$ (la solución al problema) es: \[1998-999-399+199=799\] (hay que añadir $199$ ya que estamos quitando los múltiplos de $10$ dos veces).
Informar de error en enunciado Informar de procedencia del problema
Nota. Esta es una solución sin derivadas, aunque es obvio que el problema se puede resolver fácilmente estudiando máximos y mínimos. Tenemos que \[f(x)=\frac{2x-7}{2x^2-2x-5}\ \Longrightarrow\ f'(x)=\frac{-4(x-1)(x-6)}{(2 x^2-2x-5)^2}\] luego $f'(x)=0$ sólo si $x=1$ o $x=6$. Analizando las asíntotas verticales y horizontales de $f(x)$, se puede ver que no hay valores de $f(x)$ entre el máximo local $f(6)=\frac{1}{11}$ y el mínimo local $f(1)=1$.
Informar de error en enunciado Informar de procedencia del problema
- ¿Cuantas funciones $f:A\to A$ verifican $f(f(x))=x$ para todo $x\in A$?
- ¿Cuantas funciones $f:A\to A$ verifican $f(f(f(x)))=x$ para todo $x\in A$?
- La función $f$ tiene que ser biyectiva ya que $f^{-1}=f$ ($f$ es su propia inversa), lo que nos dice que $f$ permuta los valores del conjunto $A$. Además, como $f(f(x))=x$, la función actúa sobre parejas de elementos de $A$ intercambiando sus valores o bien dejando elementos de $A$ fijos. Habrá tantas funciones $f$ como formas extraer parejas disjuntas de $A=\{1,2,3,4,5,6\}$:
- Con cero parejas hay una forma de hacerlo (dejar todo fijo).
- Con una pareja hay $\binom{6}{2}=15$ formas de hacerlo.
- Con dos parejas hay $\frac{1}{2}\binom{6}{2}\binom{4}{2}=\frac{1}{2}\cdot 15\cdot 6=45$ formas de hacerlo. El razonamiento para obtener esta fórmula es que hay $\binom{6}{2}$ formas de elegir la primera pareja y $\binom{4}{2}$ formas para la segunda (quedan sólo 4 elementos para elegir), pero estamos contando cada configuración dos veces.
- Con tres parejas hay $\frac{1}{6}\binom{6}{2}\binom{4}{2}\binom{2}{2}=\frac{1}{6}\cdot 15\cdot 6\cdot 1=15$ formas de hacerlo. El razonamiento es similar al anterior, pero estamos contado cada configuración $3!=6$ veces.
- El razonamiento para este apartado es similar. Observamos que $f$ también es biyectiva ya que cumple $f^{-1}=f\circ f$. Ahora bien, al cumplirse que $f(f(f(x)))=x$ para todo $x\in A$, se sigue que $f$ permuta cíclicamente tríos de elementos de $A$ y deja otros fijos. Ahora bien, cada trío $\{x,y,z\}$ tiene dos posibles permutaciones cíclicas según el orden en que se roten los elementos, que son $x\mapsto y\mapsto z\mapsto x$ y $x\mapsto z\mapsto y\mapsto x$. Tenemos tres casos:
- Con cero tríos hay una forma de hacerlo (dejar todo fijo).
- Con un trío hay $\binom{6}{3}=20$ formas de elegir el trío, lo que nos da 20\cdot 2=40$ posibles permutaciones.
- Con dos tríos hay $\frac{1}{2}\binom{6}{3}\binom{3}{3}=10$ formas de elegir los dos tríos, lo que nos da $10\cdot 4=40$ posibles permutaciones (hay que elegir el orden de rotación en cada trío).
Tenemos así un total de $1+40+40=81$ funciones que cumplen este apartado.
Informar de error en enunciado Informar de procedencia del problema
Sesión 2 — 17 de enero de 1998 (mañana)
Tomando $x=k$ e $y=a$, esta propiedad nos dice que $k-a$ divide a $p(k)-p(a)=7$, luego $k-a$ tiene que ser igual a $\pm 1$ o $\pm 7$, los factores enteros de $7$. Análogamente, para $x=k$ e $y=a+1$, se tiene que $k-a-1$ divide a $p(k)-p(a+1)=7$, luego $k-a-1$ tiene que ser igual a $\pm 1$ o $\pm 7$, esto es, $k-a$ tiene que ser igual a $-6$, $0$, $2$ u $8$, lo cual es absurdo (tenía que ser $\pm 1$ o $\pm 7$).
Nota. No se ha usado la hipótesis de que $p(a+2)=1$.
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Nota: $f^2(x)=f(f(x))$, $f^3(x)=f(f^2(x))=f(f(f(x)))$ y, en general, \[f^n(x)=f(f^{n-1}(x))=f(f(\ldots f(x))\ldots))\quad (n\text{ veces}).\]
Esto nos dice que, para cada $n\in\mathbb{N}$ podemos expresar $f^{n-1}(x)=x p_{n-1}(x)+1$ para cierto polinomio $g_{n-1}(x)$. Tenemos así que \begin{align*} \mathrm{mcd}(f(x),f^n(x))&=\mathrm{mcd}(f(x),f^{n-1}(f(x)))\\ &=\mathrm{mcd}(f(x),f(x) p_{n-1}(f(x))+1)=1. \end{align*}
Nota. El resultado es también cierto cambiando $f(x)=x^{1997}-x+1$ por cualquier polinomio $f(x)$ con coeficientes enteros y $f(0)=f(1)=1$. También es cierto que $f^n(y)$ y $f^m(y)$ son primos relativos para cualesquier $m,n\in\mathbb{N}$ (basta aplicar el enunciado a $x=f^{m-1}(y)$ con $n+1$ en lugar de $n$).
Informar de error en enunciado Informar de procedencia del problema
- Los vértices de un octógono regular se emparejan y se trazan los segmentos (lado o diagonal) que cada pareja determina. ¿Es posible emparejarlos de forma que los cuatro segmentos determinados tengan distintas longitudes?
- Demostrar que si se emparejan los vértices de un dodecágono regular y se trazan los segmentos que cada pareja determina, siempre habrá al menos dos con la misma longitud.
En el caso del dodecágono, para demostrar que no se puede, vamos a razonar por reducción al absurdo suponiendo que existen 6 segmentos de distinta longitud que emparejan los 12 vértices. Si numeramos los vértices consecutivamente con números del 1 al 12, habrá siempre 3 de los segmentos que unan un vértice par con uno impar mientras que los otros tres unirán par con par o bien impar con impar. Como entre 1 y 12 hay el mismo número de pares que de impares, hemos llegado a la contradicción buscada.
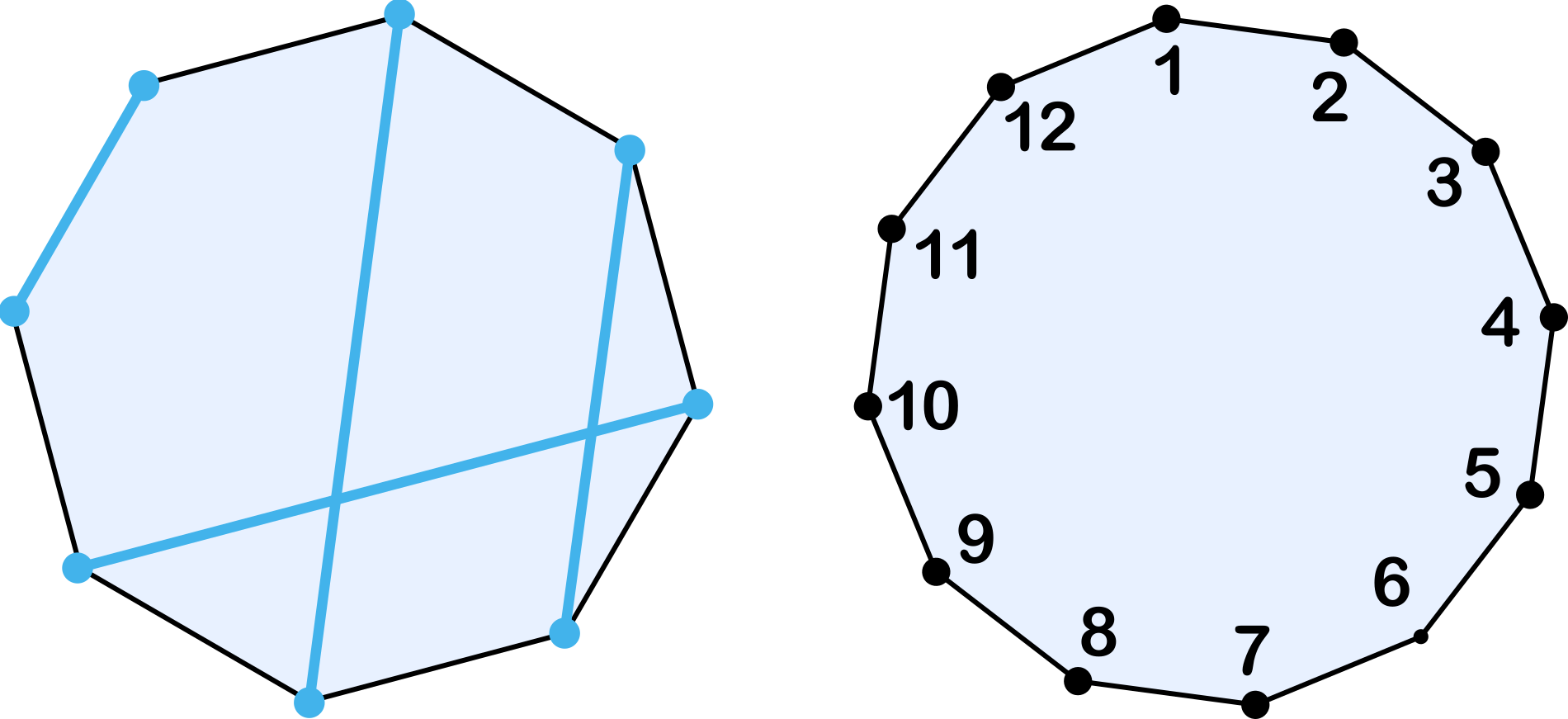
Nota. El mismo razonamiento prueba que es imposible el emparejamiento para polígonos de $8n+4$ vértices. ¿Es posible emparejar los vértices de un polígono de $8n$ lados? ¿Y los de un polígono de $4n+2$ lados?
Informar de error en enunciado Informar de procedencia del problema