Olimpiadas de Matemáticas
Página de preparación y problemas

Solución. Supondremos que $P$ contiene al menos cuatro puntos, que no pueden estar alineados ya que por ellos pasa una circunferencia. Elegimos tres puntos distintos $p_1,p_2,p_3\in P$ y tomamos la única circunferencia $\Gamma$ que pasa por ellos. Dado $p\in P$ distinto de $p_1,p_2,p_3$, el enunciado nos dice que hay una circunferencia que pasa por $p_1,p_2,p_3$ y $p$, luego no puede ser otra que $\Gamma$ ya que por $p_1,p_2,p_3$ pasa una única circunferencia. Deducimos así que $\Gamma$ contiene a todos los puntos de $P$ y la respuesta es afirmativa.

Nota. En realidad, es necesario que el enunciado diga que $P$ tiene al menos cuatro puntos o que los puntos de $P$ no están alineados. Por ejemplo, un conjunto $P$ formado por tres puntos alineados cumple la condición pero no todos los puntos de $P$ están en una circunferencia.

Solución. Llamamos $ABCD$ al cuadrilátero y $P$ al punto de intersección de sus diagonales. Supondremos que las diagonales no son perpendiculares para que las proyecciones $A',B',C',D'$ definan un cuadrilátero, luego además se cumple que $P$ se queda entre $A'$ y $C'$ en la diagonal $AC$ y también entre $B'$ y $D'$ en la diagonal $BD$. Esto demuestra que el cuadrilátero $A'B'C'D'$ es convexo y tiene las mismas rectas diagonales que $ABCD$.

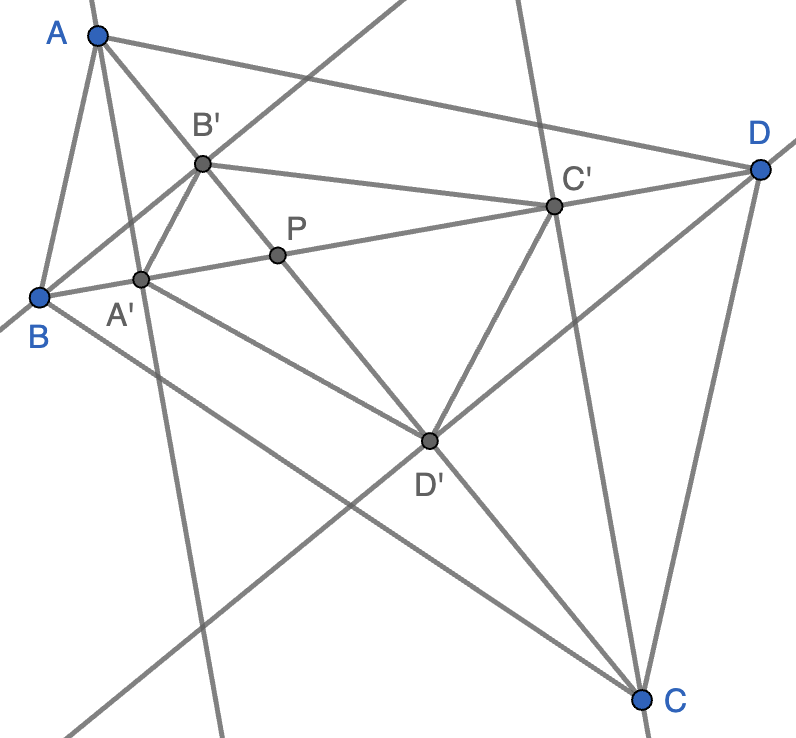
Los triángulos $AA'P$ y $BB'P$ son semejantes porque son rectángulos y tienen un ángulo común en el vértice $P$, luego se cumple que \[\frac{AP}{BP}=\frac{A'P}{B'P},\] lo que también nos dice que $ABP$ y $A'B'P$ son semejantes. De forma similar se prueba que $BCP$ y $B'C'P$ son semejantes, que $CDP$ y $C'D'P$ son semejantes y que $DAP$ y $D'A'P$ son semejantes. La razón de semejanza es la misma para los cuatro pares de triángulos ya que se tiene que $\frac{AP}{A'P}=\frac{BP}{B'P}=\frac{CP}{C'P}=\frac{DP}{D'P}$, luego el cuadrilátero $A'B'C'D'$ es semejante a $ABCD$ ya que está formado por cuatro triángulos semejantes en disposición similar. Más aún, $A'B'C'D'$ se obtiene de $ABCD$ a partir de una reflexión respecto de una de las bisectrices de las diagonales y una homotecia.

Solución. Si llamamos $y=\frac{6-x}{x+1}$, podemos despejar \[y=\frac{6-x}{x+1}\ \Longleftrightarrow \ xy=6-(x+y).\] Además, la ecuación inicial se escribe como $xy(x+y)=8$, por lo que si llamamos $s$ y $p$ a la suma y producto de las dos incógnitas, tenemos que $p=6-s$ y $sp=8$. Sustituyendo la primera en la segunda ecuación llegamos a que $s(6-s)=8$ o equivalentemente $s^2-6s+8=0$, que tiene soluciones $s=2$ y $s=4$. Distinguimos los dos casos:

• Si $s=2$, entonces $p=6-s=4$. Tenemos así que $x+y=2$ y $xy=4$, luego $x$ e $y$ son las soluciones de la ecuación $t^2-2t+4=0$. Esta ecuación no tiene raíces reales.
• Si $s=4$, entonces $p=6-s=2$, luego $x+y=4$ y $xy=2$. Por tanto, $x$ e $y$ son las soluciones de la ecuación $t^2-4t+2=0$. Esto nos da dos posibles valores de $x$, que son $x=2\pm\sqrt{2}$ y se comprueba fácilmente que cumplen la ecuación inicial.

Hemos demostrado que las únicas soluciones son $x=2+\sqrt{2}$ y $x=2-\sqrt{2}$.

Nota. Si procedemos directamente simplificando la ecuación inicial y tenemos en cuenta que $x+1\neq 0$, llegamos a la ecuación de cuarto grado $x^4-6x^3+14x^2-20x+8=0$. Esta se puede factorizar sobre los enteros como producto de dos ecuaciones de segundo grado $(x^2-4x+2)(x^2-2x+4)=0$, de donde también se deduce la solución.

Solución. Comencemos con el segundo sumando. Como $2222\equiv 3\ (\text{mod }7)$, tenemos que $2222^{5555}\equiv 3^{5555}\ (\text{mod }7)$. Ahora bien, para simplificar el exponente que, trabajando módulo $7$, tenemos que $3^1\equiv 3$, $3^2\equiv 2$, $3^3\equiv 6$, $3^4\equiv 4$, $3^5\equiv 5$ y $3^6\equiv 1$. Hemos llegado a una potencia que es congruente con $1$. Ahora si dividimos $5555$ entre $6$ obtenemos que $5555=925\cdot 6+5$, luego \[2222^{5555}\equiv 3^{5555}=(3^6)^{925}\cdot 3^5\equiv 1^{925}\cdot 5\equiv 5\ (\text{mod }7).\]

De la misma manera, se comprueba que $5555\equiv 4\ (\text{mod }7)$, luego $5555^{222}\equiv 4^{2222}\ (\text{mod }7)$. Tenemos que $4^1\equiv 4$, $4^2\equiv 2$ y $4^3\equiv 1$ módulo $7$, y hacemos la división euclídea de $2222$ entre $3$, que nos da $2222=740\cdot 3+2$. Por tanto, \[5555^{2222}\equiv 4^{2222}=(4^3)^{740}\cdot 4^2\equiv 1^{740}\cdot 2\equiv 2\ (\text{mod }7).\] Esto nos da finalmente el resultado deseado: \[2222^{5555}+5555^{2222}\equiv 5+2\equiv 0\ (\text{mod }7).\]

Solución. Sea $\Gamma$ la circunferencia que nos dan, con centro $O$ y radio $R$. El problema es equivalente a encontrar un punto $X\in\Gamma$ tal que $PQX$ sea un triángulo rectángulo con ángulo recto en $X$ pues que en tal caso bastaría prolongar los lados $PX$ y $QX$ hasta que corten en sendos puntos $Y$ y $Z$ a la circunferencia (distintos de $X$), de forma que $XYZ$ es el triángulo inscrito que buscamos. El lugar geométrico de los puntos $X$ tales que $PQX$ es rectángulo con ángulo recto en $X$ es la circunferencia de diámetro $PQ$, luego existirá el punto que buscamos si y solo si la circunferencia de diámetro $PQ$ corta a $\Gamma$ Como la circunferencia de diámetro $PQ$ tiene centro en $M$, el punto medio de $PQ$, el problema tiene solución si y solo si $OM+MP\geq R$ (observemos que $OM+MP$ es la distancia más alejada de $O$ que se puede alcanzar con la circunferencia de diámetro $PQ$).

Para terminar, vamos a expresar el resultado sin que intervenga $M$, por rizar el rizo. Tenemos que $MP=\frac{1}{2}PQ$ y que $OM$ es la mediana de $OPQ$. Usando la fórmula de la meidana, la condición que buscamos se puede escribir finalmente como \[\frac{1}{2}PQ+\sqrt{\frac{OP^2+OQ^2}{2}-\frac{PQ^2}{4}}\geq R.\]

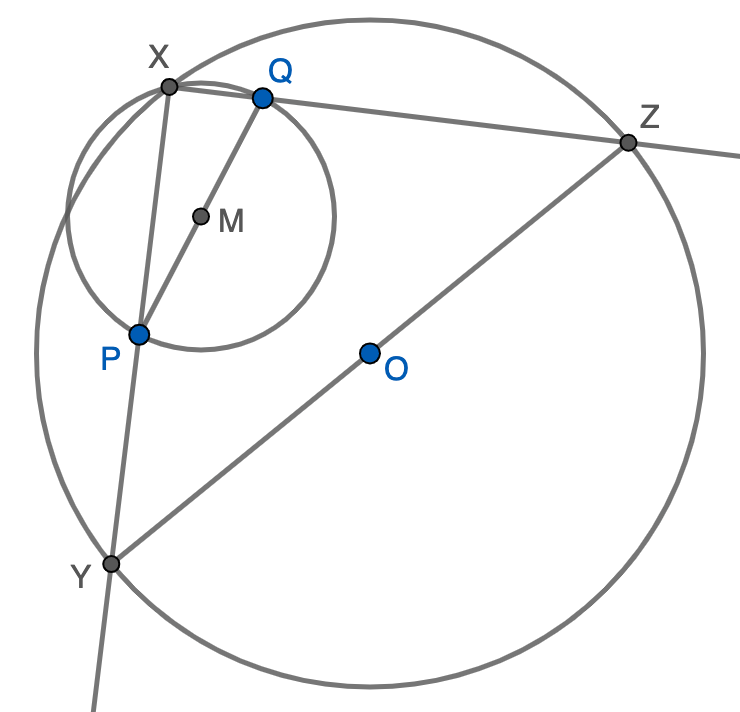
Nota. En realidad, cuando la desigualdad es estricta, hay dos soluciones ya que hay dos puntos de corte de ambas circunferencias.

Solución. La desigualdad se puede escribir de forma equivalente como \[\left(\frac{1}{a}\right)^{a^2+2ac}\left(\frac{1}{b}\right)^{b^2+2ab}\left(\frac{1}{c}\right)^{c^2+2bc}\leq 3.\] La desigualdad entre las medias aritmética y geométrica con pesos nos dice que si $x_1,x_2,x_3,w_1,w_2,w_3\geq 0$ son tales que $w_1+w_2+w_3=1$, entonces $x_1^{w_1}x_2^{w_2}x_3^{w_3}\leq w_1x_1+w_2x_2+w_3x_3$. En nuestro caso, tomaremos $x_1=\frac{1}{a}$, $x_2=\frac{1}{b}$, $x_3=\frac{1}{c}$, $w_1=a^2+2ca$, $w_2=b^2+2ab$ y $w_3^2=c^2+2bc$, que claramente verifican $w_1+w_2+w_3=(a+b+c)^2=1$. Tenemos entonces que \begin{align*} \left(\frac{1}{a}\right)^{a^2+2ac}\left(\frac{1}{b}\right)^{b^2+2ab}\left(\frac{1}{c}\right)^{c^2+2bc}&\leq \frac{a^2+2ca}{a}+\frac{b^2+2ab}{b}+\frac{c^2+2bc}{c}\\ &=3(a+b+c)=3. \end{align*}

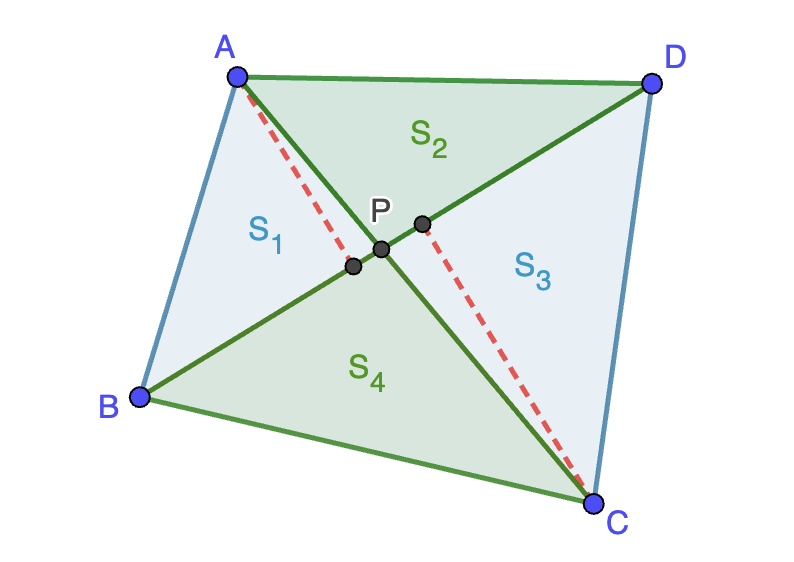
Nota. La desigualdad entre las medias aritmética y geométrica con pesos se puede ver también como la desigualdad de Jensen para la función cóncava $f(t)=\ln(t)$. La pista la da el hecho de que los exponentes sumen $1$ pero puede ser difícil darse cuenta de que hay que invertir primero para que los signos de la desigualdad vayan en el sentido correcto.

Como los pesos son todos positivos, la igualdad se alcanza sólo cuando $x_1=x_2=x_3$, es decir, cuando $a=b=c$.

Solución. El polinomio $x^5+x+1$ no tiene raíces enteras pero puede factorizarse como producto de un polinomio de grado $3$ por otro de grado $2$. Para ello, pongamos \begin{align*} x^5+x+1&=(x^3+ax^2+bx+c)(x^2+ex+f)\\ &=x^5+(a+e)x^4+(b+ae+f)x^3+(c+be+af)x^2+(ce+bf)x+cf. \end{align*} Igualando coeficientes, tenemos en primer lugar que $cf=1$, luego pondremos $c=f=1$ ya que buscamos coeficientes enteros (si no nos sale, deberíamos probar con la otra opción $c=f=-1$). Entonces, nos queda que $a+e=0$, $b+ae=-1$, $a+be=-1$ y $e+b=1$. Podemos sustituir entonces $a=-e$ y $b=1-e$ en $b+ae=-1$ para llegar a que $1-e-e^2=-1$, ecuación que tiene soluciones $e=1$ y $e=-2$. Con $e=1$, tenemos $a=-1$ y $b=0$, que cumplen la ecuación restante ($a+be=-1$) y nos dan la factorización deseada: \[x^5+x+1=(x^3-x^2+1)(x^2+x+1).\] Esto nos dice que el número original se puede factorizar (con $x=2^m$) como \[2^{5m}+2^m+1=(2^{3m}-2^{2m}+1)(2^{2m}+2^{m}+1).\] Está claro que $2^{3m}-2^{2m}\gt 0$ (puesto que $m\gt 0$), luego el primer factor no es $\pm 1$. Tampoco lo es el segundo (ya que es mayor que $1$), luego el número $2^{5m}+2^m+1$ es compuesto para todo entero $m\geq 1$.

Solución. Sea $ABCD$ el cuadrilátero convexo y $P$ el punto de corte de las diagonales. Si llamamos $S_1,S_2,S_3,S_4$ a las áreas de los cuatro triángulos en que las diagonales dividen al cuadrilátero, como se indica en la figura, entonces la propiedad de la bisección nos dice que \[S_1+S_2=S_2+S_3=S_3+S_4=S_4+S_1\ \Longleftrightarrow\ \begin{cases}S_1=S_3,\\S_2=S_4.\end{cases}\] Ahora bien, para que la diagonal $BD$ biseque, las distancias de $A$ y $C$ a la recta $BD$ deben ser las mismas (las alturas de los triángulos $ABD$ y $BCD$ de base común $BD$, indicadas con línea discontinua roja). Por lo tanto, tiene que ser $BP=DP$ para que se cumpla que $S_1=S_3$. Análogamente, se demuestra que $AP=CP$, luego hemos llegado a que las diagonales se cortan en su punto medio y esto implica que $ABCD$ es un paralelogramo.

Solución. Los enteros a considerar son de la forma $2^a\cdot 3^b\cdot 5^c\cdot 7^d$. Hay $16=2^4$ posibilidades para la paridad de los cuatro exponentes ya que cada uno de ellos puede ser par o impar. Como tenemos 17 números de esta forma, al menos dos de ellos tendrán cada uno de los cuatro exponentes con la misma paridad. Al multiplicarlos, como se suman los exponentes, obtenemos otro número de la misma forma con todos los exponentes pares, es decir, un cuadrado perfecto.

Solución. Sea $ABC$ el triángulo en cuestión y supongamos que el ángulo en $A$ está fijo y también el radio $r$ de la circunferencia inscrita, que es tangente a los lados en los puntos $X,Y,Z$, como se muestra en la figura. El área del triángulo está dada por $S=rp$, siendo $p$ el semiperímetro, luego minimizar el perímetro del triángulo equivale a minimizar su área cuando variamos $X$ en el arco mayor $YZ$. Es fácil intuir que la solución al problema es el triángulo isósceles $ARS$ tangente a la circunferencia inscrita en el punto medio $M$ de $RS$. Vamos a confirmar esta intuición viendo que cualquier otra elección de $X$ distinta de $M$ nos da un triángulo $ABC$ de área mayor que $ARS$. Si suponemos sin perder generalidad que $X$ está en el arco $MZ$ (en caso de estar en $MY$ el razonamiento es similar), probaremos que el área de $PBR$ (en verde) es menor que el área de $PCS$ (en azul), siendo $P$ el punto en de corte entre $BC$ y $RS$.

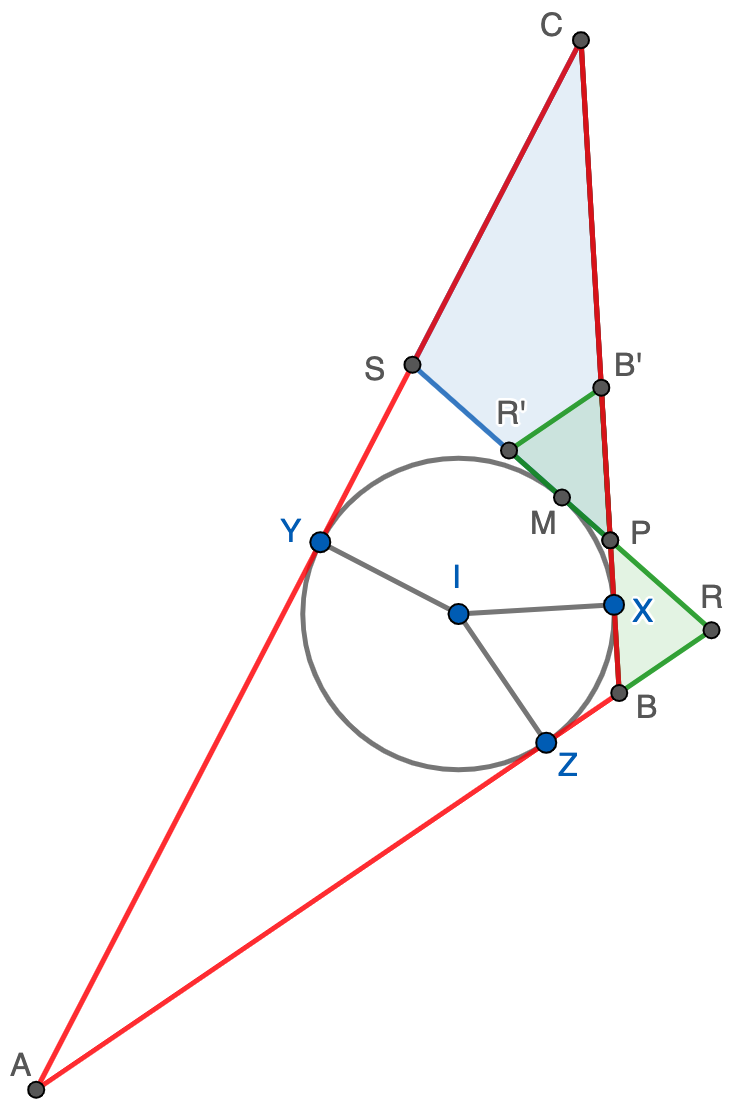
Como $P$ está en el segmento $MR$ y $M$ es el punto medio de $RS$, se sigue que $PR\lt PS$; además, se tiene que $\angle PRB$ es agudo mientras que $\angle CSR=180-\angle PRB$ es obtuso. Esto nos dice que si giramos $180^\circ$ el triángulo $PRB$ respecto de $P$ obtenemos un triángulo $PR'B'$ contenido en $PCS$, luego ciertamente el área de $PBR$ es menor que el área de $PCS$ y hemos terminado la demostración.

Solución. Un miembro concreto $A$ sólo puede estar en $6$ comités como máximo ya que hay otras $24$ personas y no puede haber dos de ellas en el mismo comité en que está también $A$. Esto nos dice que, al mirar el club al completo, hay como máximo $6\cdot 25=150$ pertenencias, pero esto nos da $150:5=30$ comités ya que cada uno lo estamos contando $5$ veces (una por cada uno de sus miembros).

Nota. Una pregunta natural es si $30$ es el número óptimo y la respuesta es que sí. Se pueden encontrar formas de distribuir los $30$ comités de $5$ miembros con un solo miembro en la intersección de cada para de ellos. Una forma muy interesante de hacerlo es tomar cada miembro del club como uno puntos $(x,y)$ de coordenadas enteras entre $0$ y $4$ (un total de $25$ puntos). Cada comité estaría formado por los puntos que cumplen la condición $ax+by\equiv c\ (\text{mod }5)$, siendo $a,b\in\mathbb{Z}$ números enteros. ¿Sabrías probar que hay exactamente $30$ comités y dos cualesquiera de ellos tienen $0$ o $1$ elementos en común?

Solución. Si aplicamos la desigualdad de Cauchy-Schwarz a los vectores \[u=\left(\sqrt{3^x},\sqrt{5^y},\sqrt{7^z}\right),\qquad v=\left(\sqrt{5^y+7^z},\sqrt{3^x+7^z},\sqrt{3^x+5^y}\right),\] obtenemos que \begin{align*} \sqrt{3^x(5^y+7^z)}+\sqrt{5^y(7^z+3^x)}+\sqrt{7^z(3^x+5^y)}&\leq\sqrt{3^x+5^y+7^z}\sqrt{(5^y+7^z)+(3^x+7^z)+(3^x+5^y)}\\ &=\sqrt{2}(3^x+5^y+7^z), \end{align*} donde hemos usado también que las exponenciales $3^x,5^7,7^z$ son números positivos. Esto nos dice que las soluciones de la ecuación son precisamente los valores que hacen de la desigualdad de Cauchy-Schwarz una igualdad. Esto equivale a que los vectores $u$ y $v$ sean proporcionales. Como están formados por números positivos, estamos buscando los $x,y,z$ tales que existe $\lambda\gt 0$ tal que \[\sqrt{3^x}=\lambda\sqrt{5^y+7^z},\qquad \sqrt{5^y}=\lambda\sqrt{3^x+7^z},\qquad \sqrt{7^z}=\lambda\sqrt{3^x+5^y}.\] Elevando al cuadrado y sumando los resultados, llegamos a que $3^x+5^y+7^z=2\lambda^2(3^x+5^y+7^z)$, luego debe ser $\lambda=\frac{1}{\sqrt{2}}$ ya que podemos cancelar $3^x+5^y+7^z\neq 0$ (recordemos que $\lambda$ es positivo). Por lo tanto, el sistema anterior nos queda \[3^x=\frac{5^y+7^z}{2},\qquad 5^y=\frac{3^x+7^z}{2},\qquad 7^z=\frac{3^x+5^y}{2}.\] Este es un sistema lineal en las incógnitas $3^x,5^y,7^z$, que es compatible indeterminado y sus soluciones son los números que verifican $3^x=5^y=7^z$. Tomando logaritmos, podemos reescribir esto como $x\log(3)=y\log(5)=z\log(7)$, luego las soluciones que buscamos pueden parametrizarse en términos de un parámetro real $a\in\mathbb{R}$ como \[(x,y,z)=\left(\frac{a}{\log(3)},\frac{a}{\log(5)},\frac{a}{\log(7)}\right).\]