Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
XLV Olimpiada Matemática Española (fase local) — 2009
Sesión 1 — 23 de enero de 2009 (mañana)
Informar de error en enunciado Informar de procedencia del problema
Nota. En realidad hemos demostrado una propiedad un poco más general: si la sección producida es un paralelogramo, entonces debe ser un rectángulo. La propiedad de ser rombo distrae más que aporta, ya que si intentamos usar argumentos sobre la longitud de los lados de $PQRS$, los razonamientos se complican y no parece que lleven a una solución sencilla.
Informar de error en enunciado Informar de procedencia del problema
Vamos a contar los caminos $x_n$ teniendo en cuenta primero las dos primeras aristas recorridas partiendo de $A$ y luego las $2n-2$ restantes para volver a $A$. Cuando hacemos recorremos una distancia 2 partiendo de $A$, tenemos nueve caminos posibles: dos acaban en $B$, dos acaban en $C$, dos acaban en $D$ y tres vuelven a $A$. Si acabamos en $B$, $C$ o $D$, para volver a $A$ en los $2n-2$ pasos restantes, tendremos $y_{n-1}$ posibles caminos ya que se trata de ir de un vértice a otro diagonalmente opuesto de la misma cara. Si estamos en $A$, tendríamos $x_{n-1}$ posibles caminos para quedarnos en $A$ tras estos $2n-2$ pasos. Esto nos da la recurrencia $x_n=3x_{n-1}+6y_{n-1}$. De la misma forma, si tras los dos primeros pasos acabamos en $A$, $C$ o $D$, para acabar en $B$ tras los $2n-2$ restantes tenemos $y_{n-1}$ posibles caminos y si estamos en $B$ tenemos $x_{n-1}$ caminos. Esto nos otra recurrencia $y_n=2x_{n-1}+7y_{n-1}$ y tenemos así el sistema \[\left\{\begin{array}{l}x_n=3x_{n-1}+6y_{n-1},\\y_n=2x_{n-1}+7y_{n-1}.\end{array}\right.\]
Veamos dos formas de terminar el problema:
- Si restamos ambas ecuaciones, obtenemos $x_n-y_n=x_{n-1}-y_{n-1}$ para todo $n$ luego la diferencia entre ambas sucesiones no varía. Como $x_1=3$ e $y_1=2$, deducimos que $x_n=y_n+1$ para todo entero positivo $n$. Para $n=500$, tenemos la respuesta: hay más caminos de longitud $1000$ que que van de $A$ a $A$ que caminos de longitud $1000$ que van de $A$ a $B$.
- La otra alternativa es probar por inducción que $x_n\gt y_n$ para todo número natural $n$, lo que en particular nos dirá que $x_{500}\gt y_{500}$. Para $n=1$, se tiene claramente que $x_1=3$ e $y_1=2$. Supuesto que se cumple que $x_{n-1}\gt y_{n-1}$ para cierto valor de $n$, también se cumple para el siguiente valor ya que \[x_n=3x_{n-1}+6y_{n-1}=2x_{n-1}+x_{n-1}+6y_{n-1}\gt 2x_{n-1}+y_{n-1}+6y_{n-1}=2x_{n-1}+7y_{n-1}=y_n.\] Esto prueba la desigualdad que queríamos y termina la demostración.
Nota. El sistema de ecuaciones en recurrencias anterior se puede resolver, aunque esto es de un nivel bastante superior al que se espera en esta olimpiada, y puede calcularse explícitamente $x_n=\frac{1}{4}(9^n+3)$ e $y_n=\frac{1}{4}(9^n-1)$.
Informar de error en enunciado Informar de procedencia del problema
Sesión 2 — 23 de enero de 2009 (tarde)
Informar de error en enunciado Informar de procedencia del problema
- Encontrar una descomposición de este tipo para el número $2009$.
- Determinar para el número $2009$ todas las posibles descomposiciones de este tipo que utilizan el menor número posible de sumandos (el orden de los sumandos no se tiene en cuenta).
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Sesión 3 — 24 de enero de 2009 (mañana)
En todos los casos, hemos probado que $n^{19}-n^7$ es múltiplo de $2$, de $3$ y de $5$, luego es múltiplo de $30$.
Nota. El polinomio original se puede seguir factorizando, aunque no aporta nada esencial a la discusión. Una factorización completa sobre los enteros es: \[n^{19}-n^7=n^7(n-1)(n+1)(n^2+1)(n^2-n+1)(n^2+n+1)(n^4-n^2+1)\]
Informar de error en enunciado Informar de procedencia del problema
- Cada plano contiene al menos cuatro de los puntos.
- Cuatro puntos cualesquiera no pertenecen a una misma recta.
- Si $P$ contiene a los 6 puntos, entonces $P$ es el único plano.
- Si $P$ contiene a 5 puntos, pongamos $A,B,C,D,E$, y no al sexto $F$, entonces el máximo número de planos es $3$, lo cual ocurre cuando hay dos rectas contenidas en $P$ que se cortan en $E$ y cada una contiene a dos de los puntos $A,B,C,D$. Tenemos entonces el plano $P$ y los otros dos planos que contienen a $F$ y a una de estas dos rectas.
- Si $P$ contiene únicamente a $A,B,C,D$ y no a los otros dos, llamémoslos $E$ y $F$, entonces cualquier otro plano debe contener necesariamente a $E$ y $F$ ya que hemos supuesto que no hay tres de los puntos $A,B,C,D$ que estén alineados. Del haz de planos que contienen a $E$ y $F$, como mucho habrá un plano que contenga a dos de los puntos $A,B,C,D$ y otro que contenga a los otros dos, luego el máximo también es $3$ en este caso.
Esto demuestra que, si queremos más de tres planos, necesariamente cada uno de ellos debe contener a tres puntos alineados. Si sólo hubiera tres puntos alineados de entre los seis, entonces tendríamos también un máximo de tres planos (que serían los que contienen a estos tres puntos y pasan por cada uno de los tres restantes). Así, nos queda la posibilidad de que los seis puntos formen dos ternas de puntos alineados (no coplanarias), en cuyo caso tenemos seis planos (los que contienen a una terna y pasan por cada uno de los tres puntos restantes). Deducimos así que el máximo es $6$.
Informar de error en enunciado Informar de procedencia del problema
Hemos probado entonces que si $m\neq 2n$ y $n\neq 2m$, tiene que ser $m=n$. Tenemos así tres casos y vamos a ver que en los tres se puede, luego la solución son los pares $(n,n)$, $(2n,n)$ y $(n,2n)$ para todo entero positivo $n$:
- Si $m=n$, sólo hay que pintar todos los puntos del mismo color.
- Si $m=2n$, podemos pintar las $n$ primeras filas enteras de blanco y las $n$ últimas filas enteras de negro.
- Si $n=2m$, análogamente pintamos las $m$ primeras columnas enteras de blanco y las $m$ últimas columnas enteras de negro.
Informar de error en enunciado Informar de procedencia del problema
Sesión 4 — 24 de enero de 2009 (tarde)
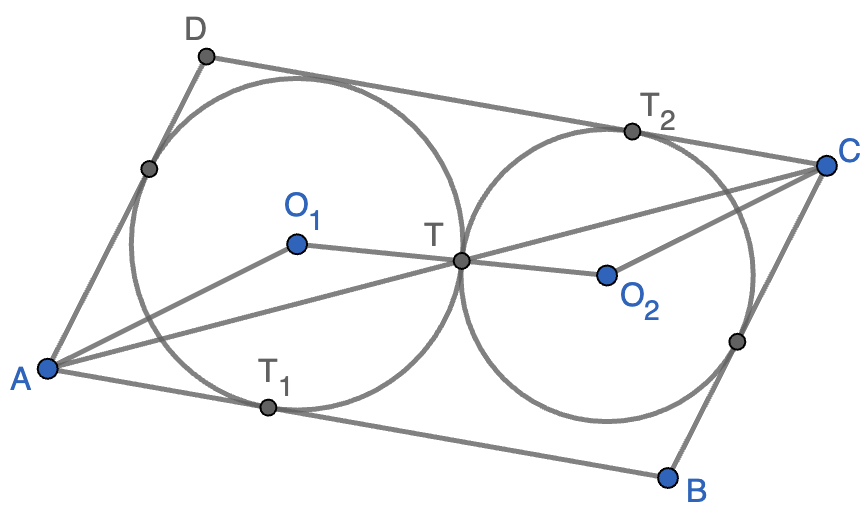
Informar de error en enunciado Informar de procedencia del problema
- Si $b-a=1$ y $2008b-2009a=1$, podemos resolver este sistema lineal para llegar a que $a=2007$ y $b=2008$, en cuyo caso se comprueba fácilmente que $x_0=1$ es raíz común a los dos polinomios del enunciado.
- Si $b-a=-1$ y $2008b-2009a=1$ (siendo $n$ impar), el sistema lineal nos da $a=-2009$ y $b=-2010$, en cuyo caso la raíz común es $x_0=-1$ (se comprueba fácilmente).
- Si $b-a=-1$ y $2008b-2009a=-1$ (siendo $n$ par), el sistema lineal nos da $a=-2007$ y $b=-2008$, en cuyo caso la raíz común es $x_0=-1$ (se comprueba también fácilmente).
Informar de error en enunciado Informar de procedencia del problema
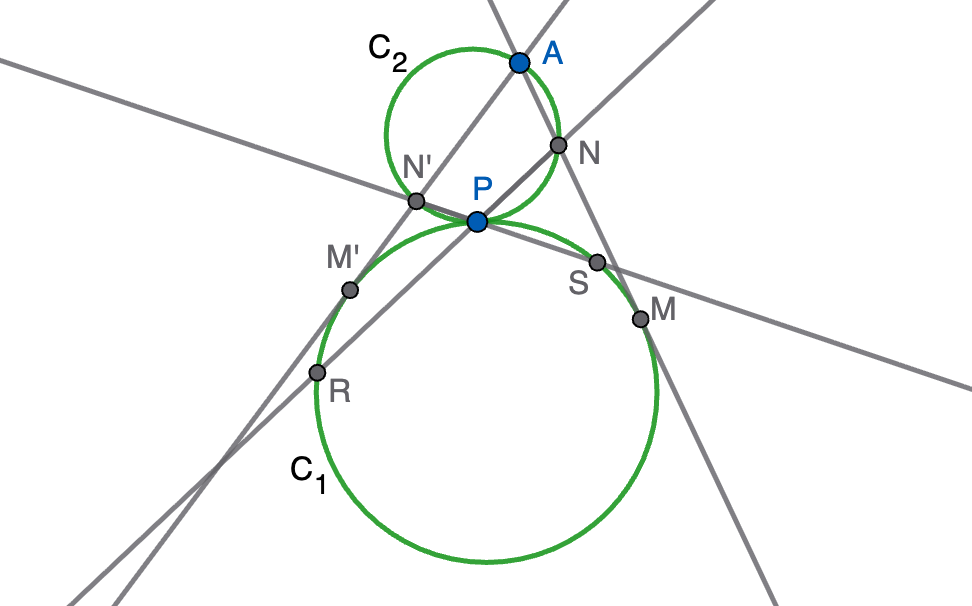
Informar de error en enunciado Informar de procedencia del problema