Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2785 problemas y 1066 soluciones.
XII Olimpiada Matemática de Centroamérica y El Caribe — 2010
Sesión 1
Problema 2093
OMCC, 2010-P1
Para cada entero positivo $n$, denotamos por $S(n)$ a la suma de sus cifras en el sistema decimal. Encontrar todas las soluciones de la ecuación
\[n(S(n)-1)=2010.\]
pistasolución 1info
Pista. Ten en cuenta que podemos descomponer en factores primos $2010=2\cdot 3\cdot 5\cdot 67$.
Solución. Descomponiendo en factores $2010=2\cdot 3\cdot 5\cdot 67$, llegamos fácilmente a que $2010$ tiene dieciséis divisores. Pueden probarse todos ellos uno a uno, pero podemos ahorrar algunos casos si nos damos cuenta de que $S(n)\equiv n\ (\text{mod }3)$, luego $n$ o $n-1$ tienen que ser múltiplos de $3$. Probamos primero los casos en que $n$ es múltiplo de $3$ y vemos que solo en uno se cumple la ecuación:
- Si $n=3$, entonces $S(n)-1=2$.
- Si $n=3\cdot 2=6$, entonces $S(n)-1=5$.
- Si $n=3\cdot 5=15$, entonces $S(n)-1=5$.
- Si $n=3\cdot 67=201$, entonces $S(n)-1=2$.
- Si $n=3\cdot 2\cdot 5=30$, entonces $S(n)-1=2$.
- Si $n=3\cdot 2\cdot 67=402$, entonces $S(n)-1=5$ (este sí es solución).
- Si $n=3\cdot 5\cdot 67=1005$, entonces $S(n)-1=5$.
- Si $n=3\cdot 2\cdot 5\cdot 67=2010$, entonces $S(n)-1=2$.
Consideremos ahora los casos en que $n-1$ es múltiplo de $3$, en los que podemos ver que no hay soluciones:
- Si $n=1$, entonces $S(n)-1=0$.
- Si $n=67$, entonces $S(n)-1=12$.
- Si $n=2\cdot 5=10$, entonces $S(n)-1=0$.
- Si $n=2\cdot 5\cdot 67=670$, entonces $S(n)-1=12$.
Deducimos así que $n=402$ es la única solución al problema.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 2094
OMCC, 2010-P2
Sea $ABC$ un triángulo y sean $L,M,N$ los puntos medios de $BC,CA,AB$, respectivamente. La recta tangente en $A$ a la circunferencia circunscrita de $ABC$ corta a $LM$ y $LN$ en los puntos $P$ y $Q$, respectivamente. Demostrar que $CP$ es paralela a $BQ$.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 2095
OMCC, 2010-P3
Una ficha se coloca en un cuadrado de un tablero $m\times n$ y se mueve de acuerdo a las siguientes reglas:
- En cada turno, la ficha se mueve a otro cuadrado que tenga un lado en común con el que ocupa en ese momento.
- La ficha no se puede quedar en un cuadrado que ya haya ocupado previamente.
- Dos movimientos consecutivos no pueden tener la misma dirección.
El juego termina cuando la ficha no puede moverse. Hallar los valores de $m$ y $n$ para los que la ficha puede colocarse inicialmente en algún cuadrado de forma que se pase por todos los cuadrados al final del juego para cierta elección de movimientos de acuerdo a las reglas anteriores.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Sesión 2
Problema 2096
OMCC, 2010-P4
Encontrar todos los enteros positivos $N$ tales que un tablero $N\times N$ se puede recubrir usando piezas de tamaño $5\times 5$ o $1\times 3$.
pistasolución 1info
Pista. Observa que si puedes recubrir un tablero $N\times N$, también puedes recubrir fácilmente un tablero $(N+3)\times(N+3)$.
Solución. Comenzamos observando que los tableros $3\times 3$ y $5\times 5$ se pueden recubrir fácilmente y tampoco es difícil dar con un recubrimiento del tablero $7\times 7$, como se muestra en la figura. Además, dado un tablero $N\times N$ que se pueda recubrir, también se puede recubrir uno de dimensiones $(N+3)\times(N+3)$ pues basta con rodearlo rellenar las columnas nuevas con fichas $1\times 3$ todas orientadas en horizontal y las casillas restantes de las tres filas nuevas con fichas $3\times 1$ todas en vertical (como se muestra en la figura de abajo). Esto nos deja solo por comprobar los tableros de tamaño $1\times 1$, $2\times 2$ y $4\times 4$, que claramente no se pueden recubrir ya que el número de casillas es menor de $25$ y no es múltiplo de $3$.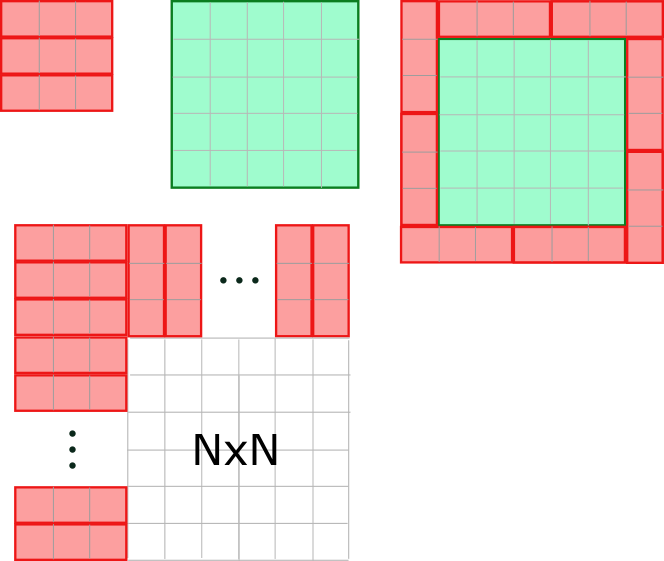

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 2097
OMCC, 2010-P5
Si $p,q,r$ son números racionales no nulos tales que $\sqrt[3]{pq^2}+\sqrt[3]{qr^2}+\sqrt[3]{rp^2}$ es también un número racional no nulo, demostrar que
\[\frac{1}{\sqrt[3]{pq^2}}+\frac{1}{\sqrt[3]{qr^2}}+\frac{1}{\sqrt[3]{rp^2}}\]
es también racional.
pista
Sin soluciones
infoPista. Puede serte útil utilizar la identidad
\[(x+y+z)^3=x^3+y^3+z^3-3(x+y+z)(xy+yz+zx)+3xyz.\]
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 2098
OMCC, 2010-P6
Sean $\Gamma$ y $\Gamma_1$ círculos que son tangentes interiormente en un punto $A$ con centros $O$ y $O_1$ y radios $r$ y $r_1$, respectivamente, con $r\gt r_1$. Sea $B$ el punto diametralmente opuesto a $A$ en $\Gamma$ y $C$ un punto en $\Gamma$ tal que $BC$ es tangente a $\Gamma_1$ en un punto $P$. Sea $A'$ el punto medio de $BC$. Si $O_1A'$ es paralela a $AP$, encontrar la razón $\frac{r}{r_1}$.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre