Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
XLVIII Olimpiada Matemática Española (fase local) — 2012
Sesión 1 — 16 de diciembre de 2011 (tarde)
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
- Con distancia $1$ sólo hay dos posibles valores del par $(j,k)$, que son $(i-1,i+1)$ e $(i+1,i-1)$, donde suponemos que los vértices se numeran cíclicamente módulo $2n$.
- Con distancia $2$ hay cuatro casos: $(i-2,i+1),(i-1,i+2),(i+1,i-2),(i+2,i-1)$.
- En general, con distancia $d$, hay $2d$ posibles elecciones del par $(j,k)$, lo que nos da un total de triángulos obtusángulos con ángulo obtuso en $A_i$ igual a \[2(1+2+3+\ldots+(n-1))=n(n-1).\]
Ahora bien, como el ángulo obtuso puede ser cualquiera de los $2n+1$ vértices y también estar en $A_i$, $A_j$ o $A_k$, tendremos que multiplicar por $3\cdot (2n+1)$ el resultado, es decir, la solución al problema es $3n(n-1)(2n+1)$.
Nota. En el enunciado se dicen ternas, término que usualmente refleja que sí importa el orden (es decir, hemos considerado que una reordenación de los mismos tres vértices nos da una terna distinta). Si queremos calcular el número de posibles elecciones de tres vértices sin importar el orden (esto es, el número de triángulos) entonces hay que dividir todos los resultado entre $3!=6$, el número de reordenaciones. De esta forma, tendríamos $n(n-1)(2n+1)$ triángulos obtusángulos.
Informar de error en enunciado Informar de procedencia del problema
Sesión 2 — 16 de diciembre de 2011 (tarde)
Informar de error en enunciado Informar de procedencia del problema
Llamamos $A$ al vértice con el ángulo recto, $B$ al vértice de $30^\circ$ y $C$ al de $60^\circ$. Sea $D$ el punto interior de $BC$ tal que $BE=\frac{3}{5}$ y trazamos la perpendicular a la hipotenusa $BC$ que pasa por $E$ y corta a $BC$ en otro punto $E$. Entonces, tenemos $ABC$ descompuesto como unión de los tres triángulos rectángulos $BDE$, $ACD$ y $BDE$, como se indica en la figura. Ahora bien, $BDE$ tiene hipotenusa $BD=\frac{3}{5}$, mientras que $ACD$ y $BDE$ comparten hipotenusa $CD$. El teorema de Pitágoras nos dice que
\begin{align*}
CD^2&=DA^2+AC^2=(AB-BD)^2+AC^2=(\mathrm{sen}(60)-\tfrac{3}{5})^2+\mathrm{cos}^2(60)\\
&=(\tfrac{\sqrt{3}}{2}-\tfrac{3}{5})^2+(\tfrac{1}{2})^2=\tfrac{34-15\sqrt{3}}{25}
\end{align*}
Tenemos que ver que este número es menor que $\frac{3}{5})^2=\frac{9}{25}$, lo que equivale a ver que $34-15\sqrt{3}\lt 9$ o, más simplificadamente, $5\lt 3\sqrt{3}$. Esto es inmediato ya que, elevando al cuadrado por ser números positivos, la desigualdad se reduce a $25\lt 27$.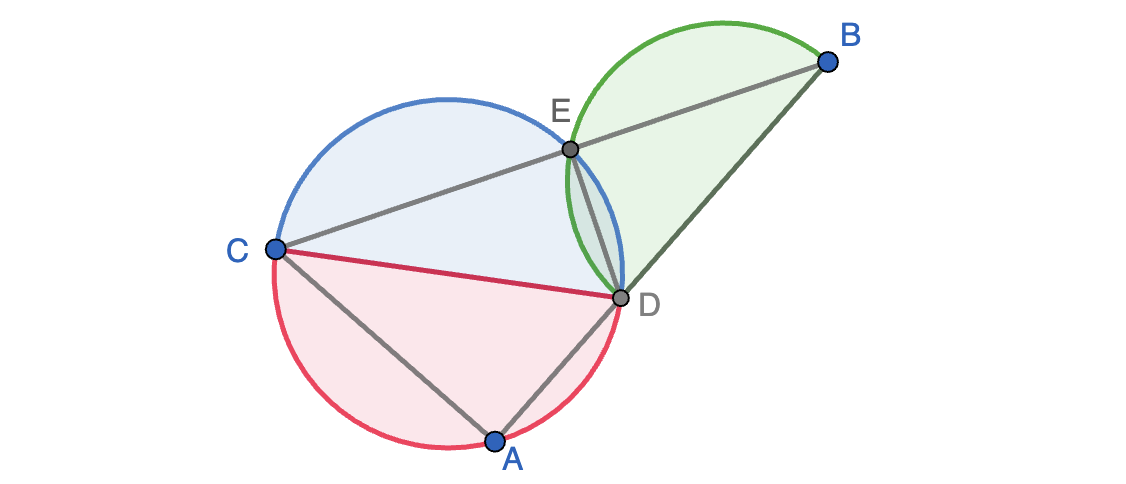
Informar de error en enunciado Informar de procedencia del problema
- Si $x\geq 90$, entonces la propiedad del arco central en la circunferencia circunscrita a $ABP$ nos dice que $\angle BO_AM=180-x$, con lo que en el triángulo rectángulo $BO_AM$ tenemos que $PH_A=BC\cot(180-x)=-BC\cot(x)$.
- Si $x\lt 90$, entonces un razonamiento similar nos dice que $PH_A=BC\cot(x)$.
- Si $x$ es obtuso, entonces los tres puntos $H_A,H_B,H_C$ están fuera de los triángulos de los que son ortocentros, luego $P$ es interior a $H_AH_BH_C$ y se tiene que $\text{Área}(H_AH_BH_C)$ es la suma de las áreas $\text{Área}(PH_AH_B)$, $\text{Área}(PH_BH_C)$ y $\text{Área}(PH_CH_A)$. Esto también se extiende al caso en que $x$ es recto, ya que se tendría que $P$ coincide con uno de los vértices de $H_AH_BH_C$ y dos de las áreas anteriores serían nulas. En ambos casos, como las cotangentes de $x,y,z$ son todas menores o iguales que cero, tenemos que \begin{align*} \text{Área}(H_AH_BH_C)&=\text{Área}(ABC)(\cot(x)\cot(y)+\cot(y)\cot(z)+\cot(z)\cot(x)\\ &=\text{Área}(ABC)\bigl(\cot(x)\cot(y)+(\cot(x)+\cot(y))\cot(360-x-y)\bigr)\\ &=\text{Área}(ABC)\bigl(\cot(x)\cot(y)-(\cot(x)+\cot(y))\cot(x+y)\bigr) \\ &=\text{Área}(ABC)\left(\cot(x)\cot(y)-(\cot(x)+\cot(y))\frac{\cot(x)\cot(y)-1}{\cot(x)+\cot(y)}\right)\\ &=\text{Área}(ABC). \end{align*}
- Si $x$ es agudo, el razonamiento es similar, solo que ahora hay que restar del área de $PH_BH_C$ las áreas de $PH_CH_A$ y $PH_AH_B$. Sin embargo, estos cambios de signo se cancelan con los cambios de signo de la cotangente de $x$ y se puede seguir al pie de la letra el cálculo del apartado anterior.
Informar de error en enunciado Informar de procedencia del problema
Sesión 3 — 17 de diciembre de 2011 (mañana)
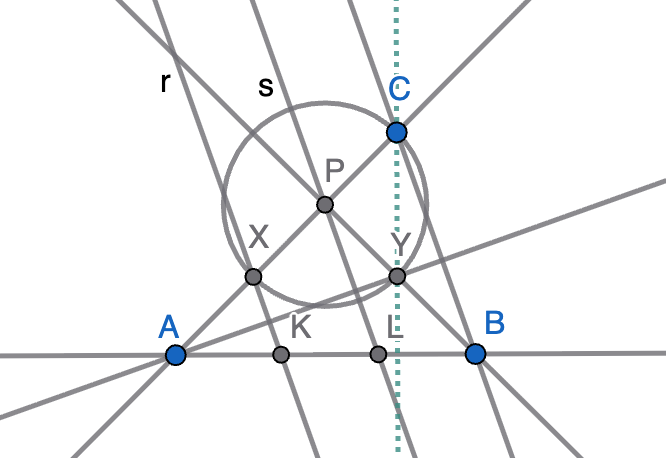
- Si $\mathrm{sen}(\alpha)=\mathrm{sen}(\beta)$ y $\mathrm{sen}(\gamma)=\mathrm{sen}(\delta)$, hay dos posibilidades. La primera es que $\alpha+\beta=180^\circ$ o bien $\gamma+\delta=180^\circ$ (en cuyo caso, $P$ está en la diagonal $AC$). La segunda es que $\alpha=\beta$ y $\gamma=\delta$; como $\alpha+\beta+\gamma+\delta=360^\circ$, se tiene que $\alpha+\delta=180^\circ$ y $P$ está sobre $BD$.
- Si $\mathrm{sen}(\alpha)=\mathrm{sen}(\delta)$ y $\mathrm{sen}(\gamma)=\mathrm{sen}(\beta)$, se razona de forma totalmente análoga y $P$ estará sobre una de las dos diagonales.
Como $P$ está sobre una de las dos diagonales, supongamos que sobre $AC$, se sigue que $P$ es el punto medio de $AC$ ya que los triángulos $PAB$ y $PBC$ tienen bases $AP$ y $CP$ y la misma altura sobre ellas, luego $AP=CP$ para que sus áreas coincidan. Además, las distancias de $B$ y $D$ a $AC$ tienen que ser la misma para que los cuatro triángulos tengan la misma área.
En resumen, la condición que nos piden es que coincidan las distancias de dos vértices opuestos del cuadrilátero a la diagonal que pasa por los otros dos vértices y que el punto $P$ sea el punto medio de dicha diagonal.
Informar de error en enunciado Informar de procedencia del problema
Ahora bien, si en la igualdad a la que queremos llegar pasamos todo al miembro de la izquierda y ponemos denominador común, tenemos que \[\frac{1}{\sqrt{A}+\sqrt{B}}+\frac{1}{\sqrt{B}+\sqrt{C}}-\frac{2}{\sqrt{A}+\sqrt{C}}=\frac{A-2B+C}{(\sqrt{A}+\sqrt{B})(\sqrt{B}+\sqrt{C})(\sqrt{A}+\sqrt{C})}=0,\] dado que $B=\frac{\pi}{3}$ y, por tanto, $A+C=\pi-\frac{\pi}{3}=\frac{2\pi}{3}$, de donde $A-2B+C=0$.
Informar de error en enunciado Informar de procedencia del problema
Ahora bien, aparte de las tangencias entre puntos del mismo piso, cada esfera del toca a tres esferas del piso inmediatamente inferior. Por ello, el número total de puntos de contacto es: \begin{align*} \text{Total}&=P_1+\ldots+P_n+3\left(1+3+6+\ldots+\frac{n(n-1)}{2}\right)\\ &=3(1^2+2^2+\ldots+n^2)-3(1+2+\ldots+n)\\ &=3\cdot\frac{n(n+1)(2n+1)}{6}-3\frac{n(n+1)}{2}=n(n-1)(n+1). \end{align*}
Nota. Hemos usado las siguientes fórmulas conocidas: \[\sum_{k=1}^nk=\frac{n(n+1)}{2},\qquad \sum_{k=1}^nk^2=\frac{n(n+1)(2n+1)}{6}.\]
Informar de error en enunciado Informar de procedencia del problema
Sesión 4 — 17 de diciembre de 2011 (tarde)
Informar de error en enunciado Informar de procedencia del problema
Un ejemplo de número positivo que cumple estas condiciones se tiene para $r=10$ y $s=2$, lo que nos da \[n=2^{10}-16^2=1024-256=768.\] Este es el número positivo más pequeño que se obtiene con $s=2$. Ahora bien, si $s\geq 5$ (que es el siguiente número congruente con $2$ módulo $3$), entonces para que $n=2^r-16^s=2^r-2^{4s}$ sea positivo, tiene que ser $r\geq 4s+1$, lo que nos da $n\geq 2^{4s+1}-2^{4s}=2^{4s}\geq 16^5\gt 768$. Deducimos por tanto que $n=768$ es el menor entero que cumple la condición del enunciado.
Informar de error en enunciado Informar de procedencia del problema
Vamos a contar ahora los triángulos obtusángulos en lugar de los acutángulos. Esto es más sencillo porque el ángulo obtuso es único y distinguible de los demás. Si suponemos que el triángulo $A_iA_jA_k$ tiene su ángulo obtuso en $A_i$, entonces $A_jA_k$ es el lado mayor y tiene que ser menor que un diámetro. Vamos a decir que la distancia entre $A_j$ y $A_k$ es $d$ si hay $d$ vértices en el arco de circunferencia $A_jA_k$, luego la distancia debe moverse entre $1$ y $n-2$ para que sea obtusángulo.
- Con distancia $1$ sólo hay dos posibles valores del par $(j,k)$, que son $(i-1,i+1)$ e $(i+1,i-1)$, donde suponemos que los vértices se numeran cíclicamente módulo $2n$.
- Con distancia $2$ hay cuatro casos: $(i-2,i+1),(i-1,i+2),(i+1,i-2),(i+2,i-1)$.
- En general, con distancia $d$, hay $2d$ posibles elecciones del par $(j,k)$, lo que nos da un total de triángulos obtusángulos con ángulo obtuso en $A_i$ igual a \[2(1+2+3+\ldots+(n-2))=(n-1)(n-2).\]
Ahora bien, como el ángulo obtuso puede ser cualquiera de los $2n$ vértices y también estar en $A_i$, $A_j$ o $A_k$, tendremos que multiplicar por $3\cdot 2n$ el resultado, es decir, tendremos un total de $6n(n-1)(n-2)$ ternas $(i,j,k)$ tales que $A_iA_jA_k$ es obtusángulo.
El número total de ternas (ordenadas) de tres elementos de un conjunto de $2n$ elementos es $2n(2n-1)(2n-2)$. Como el número de ternas que nos dan triángulos acutángulos serán las que no nos dan rectángulos ni obtusángulos, tenemos que el número buscado es \[2n(2n-1)(2n-2)-12n(n-1)-6n(n-1)(n-2)=2n(n-1)(n-2).\]
Nota. En el enunciado se dicen ternas, término que usualmente refleja que sí importa el orden (es decir, hemos considerado que una reordenación de los mismos tres vértices nos da una terna distinta). Si queremos calcular el número de posibles elecciones de tres vértices sin importar el orden (esto es, el número de triángulos) entonces hay que dividir todos los resultado entre $3!=6$, el número de reordenaciones. De esta forma, tendríamos $2n(n-1)$ triángulos rectángulos y $\frac{1}{3}n(n-1)(n-2)$ acutángulos.
Informar de error en enunciado Informar de procedencia del problema