Olimpiadas de Matemáticas
Página de preparación y problemas

Solución. Trabajando en coordenadas podemos suponer que el centro de $E$ es el origen de coordenadas y que sus semiejes están contenidos en los ejes de coordenadas, luego la elipse tiene ecuación \[\frac{x^2}{a^2}+\frac{y^2}{b^2}=1,\] donde $a,b\gt 0$ son las longitudes de los semiejes. Si cortamos esta elipse por un haz de rectas paralelas al eje $OY$, por simetría los puntos medios de los segmentos que se determinan están contenidos en el eje $OX$, luego están alineados. Vamos a ver que esto también es cierto para cualquier haz de rectas paralelas no verticales, es decir, veremos que los puntos medios de los segmentos determinado por la intersección de $E$ con las rectas forman una recta al dejar fija la pendiente $m\in\mathbb{R}$ y variar la ordenada en el origen $n\in\mathbb{R}$. Para hallar los puntos de intersección, sustituimos $y=mx+n$ en la ecuación de $E$, lo que nos da \[\frac{x^2}{a^2}+\frac{(mx+n)^2}{b^2}=1\ \Leftrightarrow\ \left(\frac{1}{a^2}+\frac{m^2}{b^2}\right)x^2+\frac{2mn}{b^2}x+\left(\frac{n^2}{b^2}-1\right)=0.\] Si la recta corta a $E$ en dos puntos $(x_1,y_1)$ y $(x_2,y_2)$, entonces $x_1$ y $x_2$ son las soluciones de la ecuación cuadrática anterior, luego la primera coordenada del punto medio que estamos buscando puede calcularse a partir de las relaciones de Cardano-Vieta para este polinomio (ver la nota): \[\frac{x_1+x_2}{2}=\frac{1}{2}\cdot\frac{-\frac{2mn}{b^2}}{\frac{1}{a^2}+\frac{m^2}{b^2}}=\frac{-m}{b^2+a^2m^2}n,\] y la segunda coordenada del punto medio será \[\frac{y_1+y_2}{2}=\frac{m(x_1+x_2)}{2}+n=\frac{-m^2n}{2(b^2+a^2m^2)}+n=\left(\frac{-m^2}{2(b^2+a^2m^2)}+1\right)n.\] Cuando $m$ está fijo, ambas coordenadas son de la forma constante por $n$, luego forman una recta (que pasa por el origen) al variar $n$ y hemos terminado.

Nota. Hemos usado concretamente que en una ecuación $ax^2+bx+c=0$, la suma de las soluciones es $\frac{-b}{a}$.

Solución. Hay cuatro formas esencialmente distintas de dividir un triángulo en tres triángulos, que está indicadas en la figura de abajo. Sin embargo, nos damos cuenta de que si un segmento termina en el interior de un lado y no es perpendicular a dicho lado, entonces forma dos ángulos suplementarios distintos. Estos dos ángulos deben ser dos de los ángulos de cada triángulo semejante pero un triángulo no puede tener dos ángulos que sumen $180^\circ$. Esto descarta directamente los casos III y IV y restringe el caso II. Veamos directamente qué restricciones adicionales nos da el hecho de que los tres triángulos deben tener ángulos iguales.

• Caso I. Tenemos un vértice interior, en el que se forman al menos dos ángulos obtusos, que deben ser iguales, y el tercero debe ser igual también ya que suma con uno de los obtusos más de $180^\circ$. Hay dos posibles configuraciones para los otros seis ángulos de los tres triángulos, que hemos llamado casos I.a y I.b. En el caso I.a, como la suma de los ángulos de $T$ es $180^\circ$, llegamos a que el ángulo verde más el amarillo suman $60^\circ$, luego $T$ es equilátero. En el caso I.b, el triángulo $T$ es isósceles, luego los ángulos amarillo y verde deben coincidir y también llegamos a que $T$ es equilátero.
• Caso II. Hay esencialmente tres configuraciones para los ángulos que no son rectos, que se indican en los casos II.a, II.b y II.c. En el caso II.a, dos verdes suman $90^\circ$, de donde se tiene que tanto el verde como el amarillo deben ser $45^\circ$ y $T$ es un triángulo rectángulo isósceles. En el caso II.b, el verde y el amarillo suman $90^\circ$, luego $T$ es en principio un triángulo rectángulo cualquiera. En el caso II.c, tenemos que $T$ es un triángulo isósceles cualquiera.

Tenemos, por tanto, que los únicos triángulos que pueden admitir la subdivisión son los triángulos rectángulos y los triángulos isósceles. Sin embargo, las subdivisiones que nos salen nos dan triángulos congruentes solamente en el caso del triángulo equilátero. Subdividiendo este último uniendo cada vértice con el centro, confirmamos que los triángulos equiláteros son las únicas soluciones.

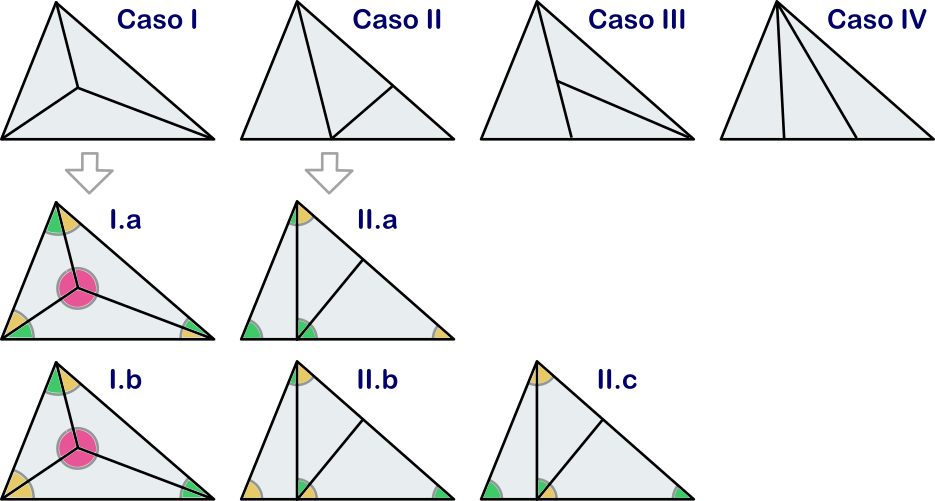
Nota. Hemos probado, de hecho, que los únicos triángulos que se pueden subdividir en tres triángulos semejantes son los triángulos rectángulos y los triángulos isósceles.

Solución. Vamos a comenzar probando que, si $0\leq e_1\lt e_2\lt\ldots\lt e_k$ son enteros, entonces se cumple que \[f(2^{e_1}+2^{e_2}+\ldots+2^{e_k})=(-1)^{e_1}+(-1)^{e_2}+\ldots+(-1)^{e_k}.\] Como todo entero positivo se expresa de forma única como suma de potencias distintas de $2$ (pensemos en el número escrito en el sistema binario), lo anterior nos determina completamente a $f$. Observamos también que $0$ es par, luego $f(0)=0$. Para ver cómo se nos puede ocurrir la fórmula anterior, véase la nota más abajo.

Vamos a probar la fórmula anterior por inducción sobre el número de sumandos $k$. Si $k=1$, entonces $f(2^{e_1})=(-1)^{e_1}f(1)$ aplicando reiteradamente la definición de $f(n)$ para $n$ par. Además, se tiene que $f(1)=f(0)+1=1$, lo que prueba que $f(2^{e_1})=(-1)^{e_1}$, como queríamos. Supongamos entonces que la igualdad es cierta para $k-1$ sumandos y demostrémosla para $k$ sumandos. Suponiendo que $e_1$ es el exponente más pequeño (como arriba), tenemos que \begin{align*} f(2^{e_1}+2^{e_2}+\ldots+2^{e_k})&=(-1)^{e_1}f(1+2^{e_2-e_1}+\ldots+2^{e_k-e_1})\\ &=(-1)^{e_1}(1+f(2^{e_2-e_1}+\ldots+2^{e_k-e_1}))\\ &\stackrel{(\star)}{=}(-1)^{e_1}(1+(-1)^{e_2-e_1}+\ldots+(-1)^{e_k-e_1})\\ &=(-1)^{e_1}+(-1)^{e_2}+\ldots+(-1)^{e_k}, \end{align*} donde en el la igualdad $(\star)$ se ha usado la hipótesis de inducción.

Teniendo en cuenta lo anterior y que $2\equiv -1\ (\text{mod }3)$ tenemos claramente el apartado (a). Si expresamos $n=2^{e_1}+\ldots+2^{e_k}$ como suma de potencias distintas de $2$, entonces \[f(n)=(-1)^{e_1}+\ldots+(-1)^{e_k}\equiv 2^{e_1}+\ldots+2^{e_k}=n\ (\text{mod }3),\] luego $f(n)$ es múltiplo de $3$ si y sólo si lo es $n$.

En cuanto al apartado (b), cada potencia de $2$ de exponente par suma una unidad y cada potencia de exponente impar resta una unidad, luego el menor $n$ tal que $f(n)=2017$ será la suma de las primeras $2017$ potencias de $2$ pares, es decir, la solución que buscamos es \[n=2^0+2^2+2^4+\ldots+2^{2\cdot 2016}=1+4+4^2+\ldots+4^{2016}=\frac{4^{2017}-1}{3},\] donde hemos usado la fórmula para la suma de los términos de una progresión geométrica.

Nota. Veamos cómo justificar la idea feliz con la que empieza la solución. Supongamos que el número $n$ está escrito en el sistema binario, únicamente con ceros y unos. Hagamos algunas observaciones previas:

• Por un lado, $n$ es par cuando su último dígito es $0$, en cuyo caso $\frac{n}{2}$ consiste en eliminar ese cero. Por lo tanto, si $n$ termina en $r$ ceros, tendremos que es múltiplo de $2^r$ y $f(n)=(-1)^rf(\frac{n}{2^r})$, donde ahora hay que calcular $f$ sobre el número $\frac{n}{2^r}$, que consiste en eliminar esos $r$ ceros de la expresión de $n$.
• Por otro lado, $n$ es impar cuando su último dígito es $1$ y ahora $n-1$ consiste en cambiar ese $1$ por un $0$. Por tanto, $f(n)=f(n-1)+1$ reduce el problema a calcular $f$ sobre un número que termina en ceros y aplicar el caso previo.
• Los pasos anteriores reducen progresivamente el número de dígitos de $n$ hasta llegar a un punto en que es necesario calcular $f(0)$. Por la propia ecuación, como $0$ es par, tendremos que $f(0)=-f(0)$, luego $f(0)=0$ necesariamente.

De esta forma, no es difícil convencerse de que para calcular $f(n)$, sólo hay que leer $f$ en binario de derecha a izquierda, sumando $1$ por cada $1$ que vayamos encontrando y multiplicando por $(-1)^{r+1}$ siempre que nos encontremos $r$ ceros seguidos. Esto se resume en que cada $1$ que aparece introduce realmente un sumando $(-1)^{s+1}$, siendo $s$ la posición en la que aparece y podemos intuir así que cada sumando $2^s$ se transforma en un sumando $(-1)^s$.

Solución. Observamos en primer lugar que $n^2$ es par si $n$ es par luego no se puede cumplir la ecuación con $n$ par. Si $n$ es impar, pongamos $n=2k-1$ para un entero positivo $k$, tenemos que $n^2+7=(2k-1)^2+7=4k^2-4k+8=4k(k-1)+8$ es múltiplo de $8$ ya que alguno de los dos números consecutivos $k-1$ o $k$ será par (en otras palabras, hemos visto sin usar congruencias que $n^2\equiv 1\ (\text{mod }8)$ precisamente cuando $n$ es impar). Por tanto, todas las soluciones están dadas en términos de un entero positivo $k$ por la fórmula \[(m,n)=\left(\frac{k(k-1)}{2}+1,2k-1\right).\] Es importante observar que se cumple que $m\gt 0$ y $n\gt 0$ tal y como se pide en el enunciado.

Buscamos ahora el menor valor de $k$ para el que $\frac{k(k-1)}{2}+1\geq 1960$, esto es, $k^2-k\geq 2\cdot 1959=3918$. Si tenemos en cuenta que debe ser $k\geq 1$, podemos despejar \[k^2-k-3920\geq 0\ \Leftrightarrow\ k\geq \frac{1+\sqrt{15673}}{2}.\] Observamos ahora que $125^2=15625$ y $126^2=15876$, luego $125\lt \sqrt{15673}\lt 126$ y esto nos dice que debe ser $k\gt \frac{1+125}{2}=63$. Por tanto, la respuesta a la pregunta del enunciado la obtenemos al tomar $k=64$, que nos da $m=\frac{k(k-1)}{2}+1=2017$ (¡el año!).

Solución. Da igual cambiar rojo por azul, así que supondremos que el $1$ está pintado de rojo. También supondremos que tenemos una coloración sin soluciones monocromáticas para obtener información. Entonces, se tiene que necesariamente $16=8(1+1)$ tiene que estar pintado de azul y $256=8(16+16)$ tiene que estar pintado de rojo. Si pintamos los números del $1$ al $15$ de rojo, los números del $16$ al $255$ de azul y los del $256$ al $2017$ de rojo, es fácil ver que no tenemos soluciones monocromáticas: por un lado, al sumar dos números rojos y multiplicar por $8$ caemos bien en el intervalo azul o bien obtenemos un resultado mayor que $2017$; por otro lado, si sumamos dos números azules y multiplicamos por $8$, obtenemos un resultado mayor o igual que $256$ que, bien es rojo o bien se pasa de $2017$.

En cuanto a la segunda, comenzamos dándonos cuenta de que el truco anterior funciona realmente para $n=2055$, pues basta pintar los números entre $2018$ y $2055$ también de rojo. El siguiente número que podemos asegurar que tiene que estar pintado de azul es $8(256+1)=2056$. Por lo tanto, supondremos que $n=2056$ y llegaremos a una contradicción si no hay soluciones monocromáticas. Esto nos dirá que $2055$ es la solución al problema.

En la igualdad $8(16+16)=8(31+1)$, el resultado tiene que ser rojo ya que $16$ es azul, con lo que $31$ tiene que estar pintado de rojo ya que $1$ es rojo. Un razonamiento similar en $8(31+16)=8(46+1)$ nos dice que $46$ está pintado de azul. Realmente, podemos reiterar este proceso para probar que $16+15k$ está pintado de azul para todo $k\geq 0$. Ahora bien, en realidad sólo podemos llegar hasta un valor de $k$ tal que $8(16+15k+1)\leq 2056$ para que el resultado de la operación no se salga del rango de números entre $1$ y $n$. En otras palabras, todos los números $16+15k$ con $k\leq 16$ tienen que estar pintados de azul. Para $k=16$ obtenemos que $256$ es azul, en contradicción con el hecho de que habíamos demostrado que $256$ tiene que ser rojo.

Solución. En el conjunto $A=(-\infty,1)\cup(1,+\infty)=\{x\in\mathbb{R}:|x|\gt 1\}$ no puede haber más de una raíz. Para probarlo, como todo polinomio tiene un número finito de raíces, habría una raíz $r$ con valor absoluto mayor o igual que el resto de raíces en $A$; si ahora $s$ es otra raíz, entonces $sr$ también es raíz según el enunciado y tiene valor absoluto $|sr|=|s|\cdot |r|\gt |r|$, contradiciendo que $r$ tiene el valor absoluto máximo. De la misma forma, se prueba que en el conjunto $B=(-1,0)\cup(0,1)=\{x\in\mathbb{R}:0\lt|x|\lt 1\}$ hay una única solución (en este caso, sólo hay que considerar la de valor absoluto mínimo).

Hemos visto así que hay un máximo de $5$ raíces: una en $A$, otra en $B$ y las otras tres serían $-1$, $0$ y $1$, los tres puntos que no están ni en $A$ ni en $B$. Sin embargo, no pueden ser las raíces a la vez ya que si $-1$ fuera una raíz y hubiera otra raíz $\alpha\in A$, entonces $-\alpha=(-1)\alpha\in A$ sería una raíz distinta en $A$. Deducimos, por tanto, que hay un máximo de $4$ raíces. Un ejemplo que prueba que $4$ es el máximo posible es el polinomio: \[p(x)=x(x-1)(x-2)(x-\tfrac{1}{2}).\]

Solución. La idea es que los números $a,b,c$ tienen que ser pequeños porque en caso de ser grandes la suma de la izquierda será menor que $1$. La expresión es simétrica en las tres variables, luego asumiremos que $a\geq b\geq c$ sin perder generalidad. Supongamos en primer lugar que $a\geq 4$. Si además se tiene que $b\geq 2$, entonces podemos acotar \[\frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{a+c}+\frac{1}{a+b+c-2}\leq\frac{1}{6}+\frac{1}{3}+\frac{1}{5}+\frac{1}{5}=\frac{9}{10}\lt 1.\] Por lo tanto, tiene que ser $b=1$ y esto nos lleva a que $c=1$. La ecuación original para $b=c=1$ se puede reescribir como $a^2-5a-2=0$, que no tiene soluciones enteras.

Lo anterior prueba que $c\leq b\leq a\leq 3$, lo que nos da sólo unas pocas posibilidades para la terna $(a,b,c)$ con $a=3$. Estas son $(3,3,3)$, $(3,3,2)$, $(3,3,1)$, $(3,2,2)$, $(3,2,1)$ y $(3,1,1)$ y se puede probar una por una que no cumplen la ecuación original. Para $a=2$ tenemos las ternas $(2,2,2)$, $(2,2,1)$ y $(2,1,1)$, de las cuales únicamente $(2,2,2)$ verifica la ecuación. Finalmente, la terna $(1,1,1)$ es la única con $a=1$ y no verifica la ecuación.

Por lo tanto, la única solución de la ecuación dada es $a=b=c=2$.

Nota. En realidad se puede refinar un poco el argumento final para no tener que probar explícitamente las diez ternas con $a\leq 3$, pero seguramente es más rápido en una olimpiada probar una por una que invertir tiempo en dar un argumento que elimine algunas de ellas.

Solución. Vamos a adaptar la demostración clásica de Euclides de que hay infinitos primos al caso de primos de la forma $3k+2$. Supongamos por reducción al absurdo que hay un número finito de tales primos y estos son $p_1,p_2,\ldots,p_r$. Distinguimos dos casos:

• Si $r$ es par, entonces el producto $p_1p_2\cdots p_r$ es congruente con $2^r\equiv 1\ (\text{mod }3)$ y consideraremos el número \[N=p_1p_2\cdots p_r+1\equiv 2\ (\text{mod }3).\] Este número no es múltiplo de $3$ ni puede tener todos sus factores congruentes con $1$ módulo $3$ (¿por qué?), luego tiene necesariamente algún factor congruente con $2$, es decir, $N$ tiene que ser divisible por alguno de los números $p_1,p_2,\ldots,p_r$, pero esto es una contradicción ya que $N$ es un múltiplo de cualquiera de ellos más una unidad.
• Si $r$ es impar, entonces $p_1p_2\cdots p_r$ es congruente con $2^r\equiv 2\ (\text{mod }3)$ y tomaremos \[N=p_1p_2\cdots p_r+3\equiv 2\ (\text{mod }3).\] De nuevo, este número ni es múltiplo de $3$ ni puede tener todos sus factores primos congruentes con $1$ módulo $3$, luego tiene algún factor primo $p_i$ de entre los números $p_1,p_2,\ldots,p_r$. En consecuencia, $p_i$ tiene que dividir a $3$, pero esto es una contradicción ya que nos diría que $p_i=3$ pero $N$ no es múltiplo de $3$.

Solución. Tomemos un plano $\Pi$ que no sea paralelo a ninguna de las rectas que unen dos de los $4n$ puntos dados (más adelante justificamos por qué existe tal plano). Consideremos un plano $\Pi_0$ paralelo a $\Pi$ tal que los $4n$ puntos quedan en uno de los semiespacios definidos por $\Pi_0$. Ahora cuando movemos $\Pi_0$ de forma paralela, va encontrando a los puntos uno a uno luego existirán planos $\Pi_1,\ldots,\Pi_n$ paralelos a $\Pi_0$ de forma que entre $\Pi_i$ y $\Pi_{i+1}$ hay exactamente cuatro puntos. Al considerar todos los segmentos que determinan tales cuatro puntos, se forma una pirámide también contenida entre $\Pi_i$ y $\Pi_{i+1}$, luego no hay intersección entre las $n$ pirámides así construidas.

Para justificar por qué existe el plano $\Pi$, consideremos las direcciones de todas las rectas que unen dos de los puntos como un conjunto $D$ finito en la esfera unidad. Habrá una circunferencia $\Gamma$ de radio $1$ contenida en la esfera que no corta a $D$: para encontrarla, basta considerar dos puntos diametralmente opuestos que no están en $D$ y el haz de círculos que pasan por esos dos puntos ya que alguno de los círculos de este haz no cortará a $D$, que es finito. Entonces, el plano $\Pi$ que contiene a $\Gamma$ no es paralelo a ninguna de las direcciones determinadas por las rectas.

Solución. La primera observación es que aplicar $m+1$ veces $f$ puede hacerse como $f\circ f^m$ o $f^m\circ f$. Ambas formas nos dan el mismo resultado, luego se cumple que \[f(n+2017)=f(f^m(n))=f^m(f(n))=f(n)+2017.\] En particular, sólo es necesario conocer $f(1),f(2),\ldots,f(2017)$ para conocer completamente la función $f$ y también se tiene que el resto de $f(n)$ módulo $2017$ sólo depende del resto de $n$ módulo $2017$. Como $f^m(n)=n+2017$, la función toma en su imagen todos los restos posibles y deducimos que la función $\theta(n)=f(n)\,\pmod{2017}$ es una biyección del conjunto $\{0,1,\ldots,2016\}$ en sí mismo.

Fijemos $n\in\{0,\ldots,2016\}$. La sucesión de restos $\{n,\theta(n),\theta^2(n),\theta^3(n),\ldots\}$ toma un número finito de valores y cada valor sólo depende del anterior, luego tiene que ser periódica. Como $\theta$ es una biyección, existirá un primer exponente $k\geq 1$ tal que $\theta^k(n)=n$, es decir, $f^k(n)$ es el primer elemento de la sucesión $\{f(n),f^2(n),f^3(n),\ldots\}$ que es congruente con $n$ módulo $2017$ y, por tanto, $f^k(n)=n+2017a$ para cierto $a\in\Z$. Entonces, tenemos que los únicos números de dicha sucesión que son congruentes con $n$ son los de la forma $f^{ck}(n)$, pero podemos calcularlos usando $(\star)$ recursivamente como \[f^{ck}(n)=f^k(f^k(\ldots(f^k(n))\ldots))=n+2017ca.\] Por lo tanto, el número $m$ que buscamos tiene que ser múltiplo de $k$ y tiene que ser $ca=1$, es decir $c=a=1$, luego no puede ser otro que $k=m$.

Con todo esto, se tiene que para cada $n$ hay exactamente $m$ restos de $\{0,1,\ldots,2016\}$ que aparecen periódicamente en la sucesión $\{n,\theta(n),\theta^2(n),\theta^3(n),\ldots\}$. Para distintos valores de $m$, estos restos son distintos, luego $2017$ tiene que poder partirse en subconjuntos de $m$ elementos y, en particular, $2017$ ser múltiplo de $m$. Como $2017$ es primo, no quedan más opciones que $m=1$ y $m=2017$. Comprobamos efectivamente que estos valores cumplen la condición, pues basta tomar $f(n)=n+2017$ si $m=1$ o bien $f(n)=n+1$ si $m=2017$.