Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2785 problemas y 1066 soluciones.
XIX Olimpiada Matemática de Centroamérica y El Caribe — 2017
Sesión 1
Problema 2147
OMCC, 2017-P1
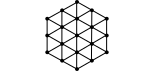
En la figura se muestra una malla hexagonal formada por triangulitos
equiláteros. Gabriel y Arnoldo toman turnos para jugar de la siguiente manera. En su turno, cada jugador colorea un segmento de recta, incluidos sus extremos, de acuerdo a las siguientes reglas:
- Los extremos del segmento deben coincidir con los vértices de algunos de los triangulitos.
- El segmento debe estar formado por uno o varios lados de algunos de los triangulitos.
- El segmento no puede tener nignún punto en común con ninguno de los segmentos coloreados anteriormente (incluidos los extremos).
Pierde el jugador que en su turno no pueda colorear ningún segmento. Si Gabriel juega primero, determinar qué jugador tiene una estrategia ganadora y describirla.
pista
Sin soluciones
infoPista. Gabriel tiene la estrategia ganadora.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 2148
OMCC, 2017-P2
Una pareja $(a,b)$ de enteros positivos con $a\lt 391$ es pupusa si
\[\mathrm{mcm}(a,b)\gt \mathrm{mcm}(a,391).\]
Hallar el valor mínimo que toma $b$ entre las posibles parejas pupusa $(a,b)$.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 2149
OMCC, 2017-P3
Dado un triángulo $ABC$, sean $D$ el pie de la altura desde $A$ y $\ell$ la recta que pasa por los puntos medios de $AC$ y $BC$. Sea $E$ el simétrico del punto $D$ respecto a $\ell$. Demostrar que el circuncentro del triángulo $ABC$ está sobre la recta $AE$.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Sesión 2
Problema 2150
OMCC, 2017-P4
Sea $ABC$ un triángulo rectángulo en $B$. Sean $B'$ el simétrico de $B$ con respecto a la recta $AC$ y $M$ el punto medio de $AC$. Se prolonga $BM$ más allá de $M$ hasta un punto $D$ de modo que $BD=AC$. Demostrar que $B'C$ es la bisectriz del ángulo $\angle MB'D$.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 2151
OMCC, 2017-P5
Susana y Brenda juegan a escribir polinomios, tomando turnos iniciando
por Susana.
- En el turno de preparación (turno 0), Susana elige un entero positivo $n_0$ y escribe el polinomio $P_0(x) = n_0$.
- Luego, en el turno 1, Brenda elige un entero positivo $n_1$ distinto de $n_0$ y escribe uno de los dos polinomios $P_1(x) = n_1x-P_0(x)$ o bien $P_1(x) = n_1x + P_0(x)$.
- En general, en el turno $k$, la jugadora correspondiente elige un entero positivo $n_k$ distinto de $n_0, n_1,\ldots, n_{k-1}$ y escribe uno de los dos polinomios: \[P_k(x) = n_kx^k − P_{k−1}(x)\quad\text{o bien}\quad P_k(x) = n_kx^k+P_{k-1}(x).\]
Gana quien escriba un polinomio que tenga por lo menos una raíz entera. Determinar qué jugadora tiene una estrategia ganadora y describir dicha estrategia.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 2152
OMCC, 2017-P6
Sea $k$ un entero mayor que $1$. Inicialmente la rana Tita se encuentra situada sobre el punto $k$ de la recta numérica. En un movimiento, si Tita se encuentra sobre el punto $n$, entonces salta al punto $f(n)+g(n)$, donde $f(n)$ y $g(n)$ son el mayor y el menor número primo (ambos positivos) que dividen a $n$, respectivamente. Determinar todos los valores de $k$ para los cuales Tita puede visitar una cantidad infinita de puntos diferentes de la recta numérica.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre