Olimpiadas de Matemáticas
Página de preparación y problemas

Solución. Usaremos la relación $DM=ab$ para escribir \begin{align*} D^2+M^2-a^2-b^2&=D^2-\frac{a^2b^2}{D^2}-a^2-b^2\\ &=\frac{D^4+a^2b^2-a^2D^2-b^2D^2}{D^2}\\ &=\frac{(a^2-D^2)(b^2-D^2)}{D^2}\geq 0. \end{align*} Aquí hemos usado que cualquier número es mayor o igual que un divisor suyo (en este caso, el máximo común divisor $D$ con el otro número). De la desigualdad anterior se deduce claramente la del enunciado.

Nota. La igualdad se alcanza sólo cuando $a=D$ o $b=D$, es decir, cuando $b$ es un múltiplo de $a$ o $a$ es un múltiplo de $b$.

Solución. Pongamos que los tres números son $a$, $ar$ y $ar^2$, donde $r$ es la razón de la progresión geométrica. Como $r=\frac{ar}{a}$ tiene que ser un número racional no nulo, podemos escribirlo como fracción irreducible $r=\frac{m}{n}$ con $m\in\mathbb{Z}$ no nulo y $n\gt 0$. Como $ar^2$ también es entero, existirá $b$ tal que $a=bn^2$. En definitiva, podemos escribir los tres números como $bn^2,bmn,bm^2$, donde $b,m,n$ son enteros. La condición del enunciado se escribe entonces como \[111=bn^2+bmn+bm^2=b(n^2+mn+m^2).\] Esto nos dice que $b$ y $n^2+mn+m^2$ son factores complementarios de $111=3\cdot 37$ y tienen que ser ambos positivos puesto que $n^2+mn+m^2=\frac{1}{2}(m^2+n^2+(m+n)^2)\gt 0$ dado que $n\gt 0$. Tenemos entonces cuatro casos posibles:

• Caso $b=111$ y $n^2+mn+m^2=1$. Obtenemos $m^2+n^2+(m+n)^2=2$ y esto sólo es posible si $(m,n)=(-1,1)$ ya que $n$ ha de ser positivo.
• Caso $b=37$ y $n^2+mn+m^2=3$. Obtenemos $m^2+n^2+(m+n)^2=6$ y, como la única forma de escribir $6$ como suma de tres cuadrados es $4+1+1$, es fácil ver que las únicas soluciones son $(m,n)=(-2,1)$, $(m,n)=(-1,2)$ y $(m,n)=(1,1)$ (las obtenemos según en que sumando pongamos el 4 recordando además que $n$ tiene que ser positivo).
• Caso $b=3$ y $n^2+mn+m^2=37$. Obtenemos $m^2+n^2+(m+n)^2=74$ y las formas de escribir $74$ como suma de tres cuadrados son $64+9+1$, $49+25+0$ y $49+16+9$ (se comprueba caso por caso). El subcaso $64+9+1$ nos lleva a que $m,n,m+n$ son los números $\pm 1,\pm 3,\pm 8$ en algún orden y se ve fácilmente que no hay solución ($\pm 8$ no es suma ni diferencia de $\pm 1$ y $\pm 3$). El subcaso $49+25+0$ tampoco tiene solución por el mismo motivo. Sin embargo, el subcaso $49+16+9$ nos da las soluciones $(m,n)=(3,4)$, $(m,n)=(4,3)$, $(m,n)=(-3,7)$, $(m,n)=(-7,3)$, $(m,n)=(-4,7)$ y $(m,n)=(-7,4)$.
• Caso $b=1$ y $n^2+mn+m^2=111$. Obtenemos $m^2+n^2+(m+n)^2=222$ y las formas de escribir $222$ como suma de tres cuadrados son $196+25+1$, $169+49+4$ y $121+100+1$. Las dos primeras no dan solución ya que $196$ y $169$ están muy alejados de los otros cuadrados como ocurría en el caso anterior. En el subcaso de $121+100+1$, tenemos las soluciones $(m,n)=(10,1)$, $(m,n)=(1,10)$, $(m,n)=(-11,1)$, $(m,n)=(-1,11)$, $(m,n)=(-11,10)$ y $(m,n)=(-10,11)$.

Cada una de estas soluciones nos da una progresión geométrica, luego tenemos una solución para $b=1$, tres para $b=3$, seis para $b=37$ y seis para $b=111$. Deducimos que hay un total de $16$ soluciones.

Solución. Aplicando la ecuación funcional, obtenemos que \[f(x+f(x+f(x+y)))=f(2x)+f(x+y).\] También podemos aplicar la ecuación funcional dos veces para desarrollar la misma expresión de un modo distinto: \begin{align*} f(x+f(x+f(x+y)))&=f(x+y+f(2x))\\ &=f(x+y+f((x+y)+(x-y)))=f(2x+2y)+x-y. \end{align*} Ahora bien, igualando ambos tenemos que \[f(2x)+f(x+y)=f(2x+2y)+x-y,\] para cualesquiera $x,y\in\mathbb{R}$. Haciendo $y=-x$, obtenemos que $f(2x)=2x$ para todo $x\in\mathbb{R}$, luego la única posible candidata a solución es la la función identidad $f(x)=x$. Se comprueba fácilmente que cumple la ecuación del enunciado, luego es realmente la única solución.

Solución. En primer lugar, vamos a determinar cuál es el lado mayor. Por un lado, \[x^4+x^3+2x^2+x+1\gt x^4+1\gt x^4-1,\] ya que $x$ es positivo. Usando que $x\gt 1$, tenemos que $x^4\geq x^3$ y $x^2\gt x$, luego \[x^4+x^3+2x^2+x+1\gt x^3+x^3+x^2+x+x+1=2x^3+x^2+2x+1.\] Sabiendo entonces que el primer lado es el mayor, tendremos que ver cuándo no supera a la suma de los otros dos, es decir, la respuesta al enunciado serán los números $x\gt 1$ tales que \[x^4+x^3+2x^2+x+1\lt (2x^3+x^2+2x+1)+(x^4-1).\] Tras simplificar y factorizar, nos queda $-x^3+x^2-x+1\lt 0$ y podemos factorizar el miembro de la izquierda para llegar a la desgualdad $(x^2+1)(1-x)\lt 0$, desigualdad que no se cumple para todo $x\gt 1$. Por tanto, para todo $x\gt 1$ hay un triángulo cuyos lados tienen las longitudes del enunciado.

Solución. La última cifra de $7^n$ es $1,7,9,3,1,7,9,3,\ldots$ para $n=0,1,2,3,4,5,6,7,\ldots$ y, como esta sólo depende de la última cifra de $7^{n-1}$, en cuanto una cifra se repite, la sucesión anterior se vuelve periódica. Deducimos así que $7^n$ tiene última cifra $3$ precisamente cuando $n=4k+3$ (ver la nota). Entonces, tenemos que \[7^{4k+3}=(7^4)^k\cdot 7^3=2401^k\cdot 343\] tendrá sus dos últimas cifras iguales a $43$ ya que $2041^k$ siempre terminará en $01$ para todo $k$.

Nota. Otra forma de ver la periodicidad de la última cifra es darse cuenta de que $7^4=2041\equiv 1\ (\text{mod }10)$, luego si dividimos $n$ entre $4$ y obtenemos que $n=4k+r$ con $0\leq r\leq 3$, se cumplirá que $7^n=(7^4)^k\cdot 7^r\equiv 1\cdot 7^r\equiv 7^r\ (\text{mod }10)$, luego las últimas cifras se repiten de $4$ en $4$. La solución también se puede terminar con el mismo cálculo observando que, de hecho, $7^4\equiv 1\ (\text{mod }100)$.

Solución. Llamemos $a,b,c$ a los lados del triángulo como es habitual y $m=AD$ a la mediana. Es bien conocida la fórmula que nos da el valor de $m$ en términos de los lados: \[m^2=\frac{b^2+c^2}{2}-\frac{a^2}{4}.\] Ahora bien, en el triángulo $ADC$, tenemos el ángulo $\angle ACD=45^\circ$ y el ángulo $\angle ADC=180^\circ-\angle ADB=135^\circ$, luego el teorema del seno nos dice que \[\frac{b}{\operatorname{sen}(135)}=\frac{m}{\operatorname{sen}(30)}\ \Longleftrightarrow\ \frac{b}{\frac{\sqrt{2}}{2}}=\frac{m}{\frac{1}{2}}\ \Longleftrightarrow\ m^2=\frac{b^2}{2}.\] Sustituyendo en la fórmula de la mediana, esto nos da $c^2=\frac{a^2}{2}$, igualdad que se puede escribir como $\frac{a/2}{c}=\frac{c}{a}$, esto es, $\frac{BD}{AB}=\frac{AB}{BC}$ y tenemos que los triángulos $ABD$ y $ABC$ son semejantes (tienen un ángulo igual y los lados adyacentes proporcionales). Deducimos así que $\angle BAD=\angle ACB=30^\circ$.

Solución. Podemos elegir un sistema de coordenadas en el espacio para escribir la esfera mediante la ecuación $x^2+y^2+z^2=r^2$, de forma que las caras del cubo estén en los planos $x=\pm r$, $y=\pm r$ y $z=\pm r$. Tomando un punto $(x_0,y_0,z_0)$ de la esfera, vamos a suponer por simetría que está en el primer octante y, por tanto, cumple $0\leq x_0,y_0,z_0\leq r$. Con esto podemos responder fácilmente a las preguntas propuestas

1. La suma de las distancias a las caras es \[(r-x_0)+(r+x_0)+(r-y_0)+(r+y_0)+(r-z_0)+(r+z_0)=6r,\] que no depende del punto (en realidad, esto es cierto para cualquier punto interior al cubo, no tiene ni por qué estar en la esfera).
2. La suma de los cuadrados de las distancias es \begin{align*} (r-x_0)^2+&(r+x_0)^2+(r-y_0)^2+(r+y_0)^2+(r-z_0)^2+(r+z_0)^2\\ &=6r^2+2(x_0^2+y_0^2+z_0^2)=6r^2+2r^2=8r^2, \end{align*} que tampoco depende del punto.
3. Finalmente, la suma de los cubos de las distancias es \begin{align*} (r-x_0)^3+&(r+x_0)^3+(r-y_0)^3+(r+y_0)^3+(r-z_0)^3+(r+z_0)^3\\ &=6r^3+3(x_0^2+y_0^2+z_0^2)=6r^3+3r^2=9r^3, \end{align*} donde hemos podido cancelar por parejas los términos de grado $1$ y $3$ en las variables $x_0,y_0,z_0$.

Nota. Lo mismo ya no es cierto para potencias de exponente $n\geq 4$. Por ejemplo, para $r=1$, el punto $(1,0,0)$ tiene suma de potencias $n$-ésimas de las distancias igual a $2^n+4$ y para punto $(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}},0)$ esta suma es $2(1-\frac{1}{\sqrt{2}})^2+2(1+\frac{1}{\sqrt{2}})^n+2$. Este último número no es entero para $n\geq 6$ y es igual a $19$ para $n=4$ y a $31$ para $n=5$, luego no coincide con $2^n+4$.

Solución. Demostraremos que el número es múltiplo de $a$ (el mismo argumento también prueba que es múltiplo de $b$ y de $c$). Como $(ab)^{c-1}$ y $(ca)^{b-1}$ son múltiplos de $a$ ya que los exponentes son enteros positivos, tendremos que ver que $(bc)^{a-1}-1$ es múltiplo de $a$. Ahora bien, como los tres primos son distintos, se cumple obviamente que $\mathrm{mcd}(bc,a)=1$ y el teorema pequeño de Fermat nos asegura que $(bc)^{a-1}\equiv 1\ (\text{mod }a)$, lo cual equivale a que $(bc)^{a-1}-1$ es múltiplo de $a$ y así hemos terminado.

Solución. Señalamos $16$ cuadrados $2\times 2$ como indica la figura, que cubren un total de $64$ casillas. Si pintamos $33$ o más de ellas, por el principio del palomar, en alguno de los $16$ cuadrados tendremos que haber pintado más de dos casillas, luego hemos pintado una figura con la forma de la del enunciado. Supondremos entonces que hemos pintado un máximo $32$ de dichas $64$ casillas. En otras palabras, habremos pintado al menos $14$ de las $17$ casillas restantes, es decir, habremos dejado sin pintar a lo sumo $3$ de ellas. Por lo tanto, alguna de las cuatro figuras moradas debe estar pintada completamente.

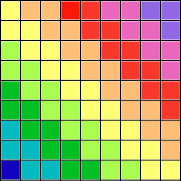
Nota. El número $46$ es óptimo ya que sí que se pueden pintar $45$ casillas de forma que no haya tres casillas pintadas en forma de L. Por ejemplo, se pueden pintar las filas impares o bien las columnas impares. ¿Sabrías probar que estas son las únicas formas de pintar $45$ casillas para que no haya tres pintadas en forma de L?