Olimpiadas de Matemáticas
Página de preparación y problemas

Solución. Podemos suponer que el número inicial es impar, porque de no serlo se transforma en un impar tras sucesivas divisiones entre 2. Nos fijamos en que si $n$ es múltiplo de $5$, entonces al aplicar la operación el número de veces que queramos siempre obtendremos un múltiplo de $5$, luego no se puede llegar a $1$.

Si $n$ no es múltiplo de $5$, entonces nunca se obtiene un múltiplo de $5$ en el proceso. Para $n=3$, tenemos $3\mapsto 8\mapsto 4\mapsto 2\mapsto 1$ y, para $n\geq 7$, al ser $n$ impar, los primeros pasos serán $n\mapsto n+5\mapsto\ldots\mapsto \frac{n+5}{2^k}$ siendo $\frac{n+5}{2^k}$ impar. Como $\frac{n+5}{2^k}\lt n$ por ser $n\geq 7$ y $k\geq 1$, reducimos el problema al de un impar más pequeño. Deducimos así que el proceso siempre termina para cualquier $n$ que no es múltiplo de $5$.

Solución. Para cada $k$, consideramos $S_k=a_k+a_{k+1}+\ldots+a_{k+1008}$, donde los subíndices los consideramos cíclicamente módulo $2020$ (es decir, $a_{2020+i}=a_{i}$ para todo $i$). Dado que entre todas las sumas $S_1,S_2,\ldots, S_{2020}$ aparece $1009$ veces cada término $a_i$, tenemos que la suma $S$ de los 2020 elementos verifica \[1009S=S_1+S_2+\ldots+S_{2020}\gt 0\] y de aquí se deduce que $S\gt 0$.

Solución. La idea clave es darse cuenta de que la segunda ecuación se puede escribir equivalentemente como $(x-y)(y-z)(x-z)=0$, lo que nos dice que dos de las incógnitas tienen que ser iguales. Como no hay simetría, tendremos que distinguir tres casos:

• Si $x=y$, entonces la primera ecuación nos dice que $2x+z=1$. Sustituyendo $y=x$ y $z=1-2x$ en la tercera y simplificando, llegamos a la ecuación $3x^2-x=0$, que nos da soluciones $x=0$ y $x=\frac{1}{3}$. Deshaciendo las sustituciones, obtenemos la soluciones al sistema original $(x,y,z)=(0,0,1)$ y $(x,y,z)=(\frac{1}{3},\frac{1}{3},\frac{1}{3})$.
• Si $y=z$, la primera ecuación nos da $x+2y=1$, luego podemos sustituir $z=y$ y $x=1-2y$ en la tercera ecuación y después de simplificar nos queda $y(3y^2-4y+1)=0$, que tiene soluciones $y=0$, $y=1$ e $y=\frac{1}{3}$. En el sistema original, esto se corresponde con las soluciones $(1,0,0)$, $(-1,1,1)$ y $(\frac{1}{3},\frac{1}{3},\frac{1}{3})$, aunque esta última ya la hemos obtenido previamente.
• Si $z=x$, procedemos de forma análoga usando la primera ecuación para obtener $y=1-2x$. Sustituyendo en la tercera y simplificando, llegamos a que $x(9x^2-9x+2)=0$, ecuación que tiene por soluciones $x=0$, $x=\frac{1}{3}$ y $x=\frac{2}{3}$. Estas nos dan las soluciones del sistema $(0,1,0)$, $(\frac{1}{3},\frac{1}{3},\frac{1}{3})$ y $(\frac{2}{3},\frac{-1}{3},\frac{2}{3})$.

Se han obtenido así un total de $7$ soluciones distintas.

Solución. Hay que probar dos implicaciones. La más sencilla consiste en suponer que $a=b=c$, en cuyo caso para cualquier $x\in\mathbb{R}$ se cumple que \[p(x)=(x-a)(x-b)+(x-b)(x-c)+(x-c)(x-a)=3(x-a)^2\geq 0.\] Recíprocamente, supongamos que $p(x)\geq 0$ para todo $x\in\mathbb{R}$. Podemos simplificar el polinomio operando todos los paréntesis y luego completar cuadrados para obtener que \begin{align*} p(x)&=x^2-ax-bx+ab+x^2-bx-cx+bc+x^2-cx-ax+ca\\ &=3x^2-2(a+b+c)x+(ab+bc+ca)\\ &=3\left(x^2-\tfrac{1}{3}(a+b+c)\right)^2-\tfrac{1}{3}(a+b+c)^2+(ab+bc+ca). \end{align*} Por tanto, este polinomio toma su mínimo valor en $x=\frac{1}{3}(a+b+c)$ y esto nos dice que $p(\frac{1}{3}(a+b+c))\geq 0$. De esta manera \begin{align*} 0\leq 3\, p(\tfrac{1}{3}(a+b+c))&=-(a+b+c)^2+3(ab+bc+ca)\\ &=-(a^2+b^2+c^2)-2(ab+bc+ac)+3(ab+bc+ca)\\ &=-(a^2+b^2+c^2)+(ab+bc+ac)\\ &=-(a-b)^2-(b-c)^2-(c-a)^2. \end{align*} La única forma de que se cumpla esta desigualdad es que $a-b=b-c=c-a=0$, es decir, que $a=b=c$, como queríamos demostrar.

Solución. Sean $F$ y $G$ los puntos en que la circunferencia inscrita es tangente a los lados $AB$ y $AC$, respectivamente. Como $P$ está en la bisectriz $CI$, está a la misma distancia de $G$ y de $D$, luego hay una circunferencia de centro $P$ que pasa por $G$ y $D$, que corta de nuevo a los lados $BC$ y $AC$ en puntos $H$ y $J$, respectivamente, como se muestra en la figura. También está claro que hay una circunferencia de centro $B$ que pasa por $D$ y $F$. Vamos a ver que $AD$ es el eje radical de ambas circunferencias, luego será perpendicular a $BP$, la recta que une sus centros.

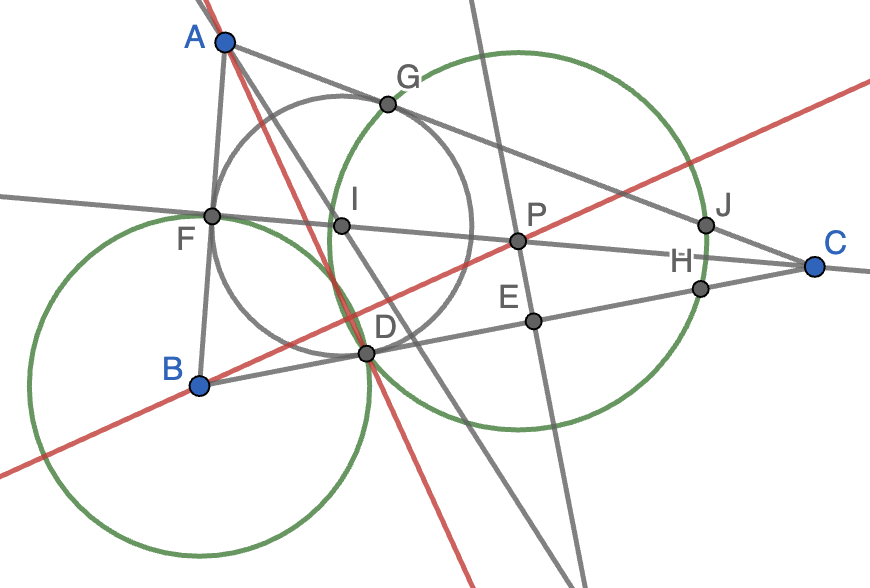
Para ver esto, será suficiente ver que $A$ tiene la misma potencia respecto de ambas circunferencias. La potencia de $A$ respecto de la circunferencia de centro $B$ es $AF\cdot(AF+2BF)$. La potencia de $A$ respecto de la circunferencia de centro $P$ es $AG\cdot AJ$. Ahora bien, tenemos que $AG=AF$ por estar $A$ en la bisectriz del ángulo $A$ y $GJ=DH$ por estar $P$ en la bisectriz del ángulo $C$. Además, $DH=2DE$ por ser $E$ el pie de la perpendicular a la cuerda $DH$ desde el centro $P$ y, finalmente, $DE=BD$ por la hipótesis del enunciado. Tenemos así que $AG\cdot AJ=AF\cdot(AF+2BF)$, como queríamos demostrar.

Solución. Vamos a probar que $AB^2+DP^2=AP^2+BD^2$, lo que implica que las dos diagonales del cuadrilátero $ABDP$ (sombreado en azul) son perpendiculares y se tiene el resultado deseado. Sea $X$ el pie de la perpendicular por $P$ al lado $AC$. Usando que $PX=PE$ y $BD=BE$, así como el teorema de Pitágoras en los triángulos rectángulos $AXP$ y $DPE$, tenemos que \[AB^2+DP^2=AB^2+DE^2+PE^2=AB^2+BD^2+PX^2=BD^2+AP^2+AB^2-AX^2,\] luego será suficiente con probar que $AB=AX$.

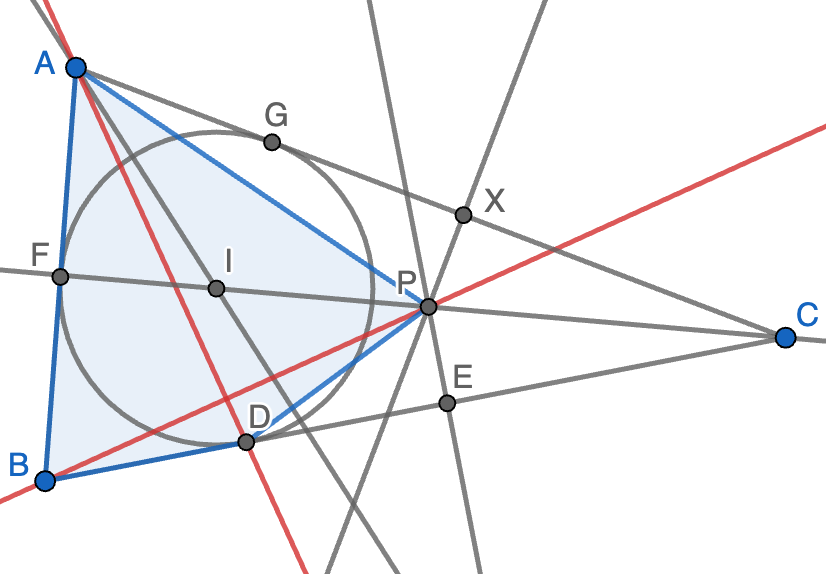
Para ello, sean $F$ y $G$ los puntos en que la circunferencia inscrita es tangente a los lados $AB$ y $AC$, respectivamente. Usando que $CX=CE$, $BF=BD=DE$, $AF=AG$ y $CG=CD$, tenemos que \[AX=AC-CX=AG+CG-CE=AF+CG-CD-BD+2BD=AF+BF=AB.\]

Solución. Pongamos que el polígono tiene $n$ lados y escribamos sus ángulos internos como $a,a+d,\ldots,a+(n-1)d$, siendo $d$ la diferencia de la progresión aritmética. Como la suma de los ángulos internos de un $n$-gono es $180(n-2)$ (ya que se puede triangularse en $n-2$ triángulos), deducimos que \[180(n-2)=a+(a+d)+\ldots+(a+(n-1)d)=na+\frac{n(n-1)}{2}d.\] Por tanto, tenemos que resolver la ecuación diofántica \[360(n-2)=2na+n(n-1)d\ \Leftrightarrow\ 2a+(n-1)d=360-\frac{720}{n}.\] Esto acota los valores de $n$ a los divisores de $720$ (mayores o iguales que $3$). Además, para que el polígono sea convexo, sus ángulos tienen que ser menores que $180$, lo que nos dice que el mayor ha de serlo, es decir, $a\lt 180-(n-1)d$. Sustituyendo en la ecuación diofántica, la convexidad se traduce en que $720=(360-2a-(n-1)d)n\gt n(n-1)d\geq n(n-1)$, donde hemos usado que $d\geq 1$ porque nos dicen que no todos los ángulos son iguales. Esto último se traduce en que $3\leq n\leq 27$ y $d\lt\frac{720}{n(n-1)}$.

La idea ahora es que, para cada divisor $3\leq n\leq 27$ de $720$, estudiaremos si existe un par de enteros positivos $(a,d)$ verificando simultáneamente $2a+(n-1)d=360-\frac{720}{n}$ y $d\lt\frac{720}{n(n-1)}$. Lo haremos caso por caso ya que no son muchos

• Si $n=3$, tenemos $2a+2d=120$ y $d\lt 120$. Una solución es $a=d=30$.
• Si $n=4$, tenemos $2a+3d=180$ y $d\lt 60$. Una solución es $a=75$, $d=10$.
• Si $n=5$, tenemos $2a+4d=216$ y $d\lt 36$. Una solución es $a=100$, $d=4$.
• Si $n=6$, tenemos $2a+5d=240$ y $d\lt 24$. Una solución es $a=100$, $d=8$.
• Si $n=8$, tenemos $2a+7d=270$ y $d\lt 13$. Una solución es $a=100$, $d=10$.
• Si $n=9$, tenemos $2a+8d=280$ y $d\lt 10$. Una solución es $a=120$, $d=5$.
• Si $n=10$, tenemos $2a+9d=288$ y $d\lt 8$. Una solución es $a=135$, $d=2$.
• Si $n=12$, tenemos $2a+11d=300$ y $d\lt 6$. Una solución es $a=139$, $d=2$.
• Si $n=15$, tenemos $2a+14d=312$ y $d\lt 4$. Una solución es $a=149$, $d=1$.
• Si $n=16$, tenemos $2a+15d=315$ y $d\lt 3$. Una solución es $a=150$, $d=1$.
• Si $n=18$, tenemos $2a+17d=320$ y $d\lt 3$. Una solución es $a=143$, $d=2$.
• Si $n=20$, tenemos $2a+19d=324$ y $d\lt 2$. En este caso sólo nos queda $d=1$ y no hay solución puesto que el miembro de la derecha sería par y el de la izquierda impar.
• Si $n=24$, tenemos $2a+23d=330$ y $d\lt 2$. Tampoco hay solución por el mismo motivo que en el caso anterior.

Deducimos así que los posibles valores de $n$ son $3$, $4$, $5$, $6$, $8$, $10$, $12$, $15$ y $18$.

Solución. Supongamos que $n\equiv 2\ (\text{mod }3)$ y $d$ es un divisor suyo. Como $d$ no puede ser múltiplo de $3$ (en tal caso, $n$ también lo sería), llegamos a que $d\equiv 1\ (\text{mod }3)$ o bien $d\equiv 2\ (\text{mod }3)$. Su divisor complementario $\frac{n}{d}$ tiene que cumplir $\frac{n}{d}\equiv 2\ (\text{mod }3)$ o bien $\frac{n}{d}\equiv 1\ (\text{mod }3)$, respectivamente, para que $d\cdot\frac{n}{d}=n\equiv 2\ (\text{mod }3)$. Por tanto, tenemos que $d+\frac{n}{2}\equiv 1+2\equiv 0\ (\text{mod }3)$.

De esta manera, en la suma de divisores, tras agrupar cada divisor con su complementario, tendremos una suma de múltiplos de $3$ y hemos resuelto el problema. Sin embargo, queda por ver que todos los divisores están emparejados, lo cual es cierto a no ser que $n$ sea un cuadrado perfecto (en cuyo caso $d=\sqrt{n}$ coincide con su complementario $\frac{n}{d}=\sqrt{n}$). Como todo cuadrado es congruente con $0$ o $1$ módulo $3$, este caso no se da nunca.

Solución. Observamos en primer lugar que, para cualquier entero positivo $k$, se tiene que $\frac{k+2}{k(k+1)(k+3)(k+4)}=\frac{1}{6k(k+1)}-\frac{1}{6(k+3)(k+4)}$ (ver la nota más abajo). Por lo tanto, podemos expresar \begin{align*} \frac{3}{1\cdot 2\cdot 4\cdot 5}&=\frac{1}{6\cdot 1\cdot 2}-\frac{1}{6\cdot 4\cdot 5},\\ \frac{4}{2\cdot 3\cdot 5\cdot 6}&=\frac{1}{6\cdot 2\cdot 3}-\frac{1}{6\cdot 5\cdot 6},\\ \frac{5}{3\cdot 4\cdot 6\cdot 7}&=\frac{1}{6\cdot 3\cdot 4}-\frac{1}{6\cdot 6\cdot 7},\\ &\vdots\\ \frac{n+2}{n(n+1)(n+3)(n+4)}&=\frac{1}{6n(n+1)}-\frac{1}{6(n+3)(n+4)} \end{align*} Si sumamos todas estas igualdades, en el miembro de la derecha se simplifican casi todos los sumandos menos los tres primeros y los tres últimos. Con lo cual la suma del enunciado es igual a \[S=\frac{1}{6\cdot 1\cdot 2}+\frac{1}{6\cdot 2\cdot 3}+\frac{1}{6\cdot 3\cdot 4}-\frac{1}{6(n+1)(n+2)}-\frac{1}{6(n+2)(n+3)}-\frac{1}{6(n+3)(n+4)}\] Si hacemos todas las operaciones, esta suma puede simplificarse como \[S=\frac{n(n+5)}{8(n+1)(n+4)}.\]

Nota. Se trata de una suma telescópica en la que cada sumando se escribe como diferencia de dos términos, de forma que al sumar estos términos se cancelan casi todos. Una forma de hacer esto (que funciona con cualquier suma cuyo término general es racional y cuyo denominador tiene raíces enteras simples) es escribir \[\frac{n+2}{n(n+1)(n+3)(n+4)}=\frac{A}{n}+\frac{B}{n+1}+\frac{C}{n+3}+\frac{D}{n+4}\] y resolver las variables $A,B,C,D\in\mathbb{R}$ para que la igualdad sea cierta para todo $n$. En este caso, se tiene que $A=-B=C=-D=\frac{1}{6}$ y pueden agruparse los sumandos por parejas (aunque no es necesario hacerlo así en general). Al sumar en la igualdad anterior, salvo el factor $\frac{1}{6}$, se suman y restan inversos de enteros. Cancelándolos convenientemente se obtiene el resultado de arriba.