Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
LVII Olimpiada Matemática Española (fase local) — 2021
Sesión 1 — 21 de enero de 2021 (mañana)
Informar de error en enunciado Informar de procedencia del problema
- Comenzamos observando que no puede ser $n\lt m$ ya que entonces hay $m$ filas y cada una tiene entre $0$ y $n-1\lt m-1$ filas coloreadas; por el principio del palomar, debería haber dos filas con el mismo número de casillas coloreadas.
- Consideremos ahora el caso $n=m$, en el que tenemos que el número de casillas coloreadas en las distintas filas debe ser $0,1,2,\ldots,m-1$ en algún orden, luego el número total de casillas coloreadas es $0+1+2+\ldots+(m-1)=\frac{(m-1)m}{2}$. Como cada columna tiene el mismo número de casillas coloreadas, este número debe ser $\frac{m-1}{2}$, que solo es entero si $m$ es impar. Deducimos así que la coloración es imposible si $n=m$ es impar. El caso par, por el contrario, si se puede colorear: podemos dejar la primera fila vacía, en la segunda pintar la casilla de más a la izquierda, en la tercera las $m-1$ casillas de más a la derecha, en la cuarta las dos casillas de más a la derecha, en la quinta las $m-2$ de más a la derecha, y así sucesivamente. En la figura superior vemos esta coloración para $(m,n)=(9,9)$.
- Vamos a ver ahora que en el caso $n\gt m$ la coloración siempre es posible. Si $m$ es impar, basta seguir la estrategia descrita en el párrafo anterior (la diferencia es el número de casillas pintadas en cada fila no recorrerá todos los valores entre $0$ y $m-1$). Si $m$ es par, entonces podemos hacer lo mismo eliminando la primera fila en la que no estaba pintada ninguna casilla. En la figura central vemos esta coloraciones para $(m,n)=(7,10)$ y en la inferior para $(m,n)=(6,10)$ a modo de ejemplo.

Informar de error en enunciado Informar de procedencia del problema
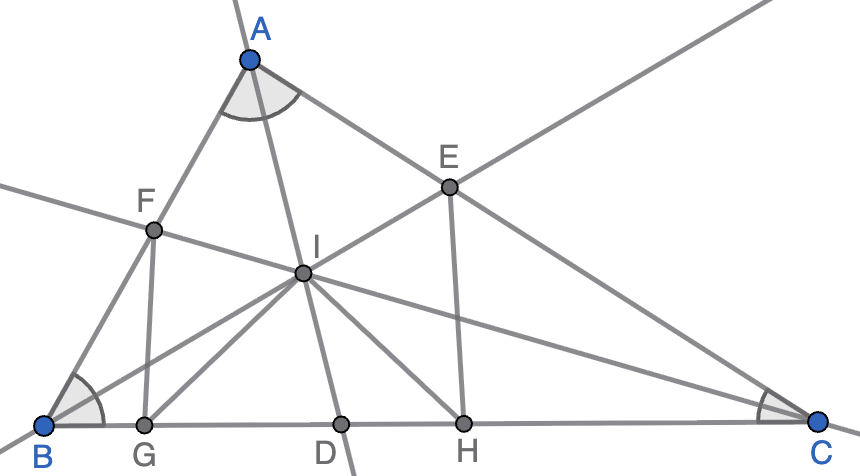
Está claro que los mismos argumentos funcionan para demostrar que $\angle DHE=\angle IHE=\alpha$, luego $\angle BHE=2\alpha$ y hemos terminado.
Informar de error en enunciado Informar de procedencia del problema
- Se cumple que $s_0=1$ ya que la única solución de $t_1+t_2+\ldots+t_n=0$ es $t_1=t_2=\ldots=t_n=0$. De la misma forma, $s_{2n}=1$ ya que la única solución de $t_1+t_2+\ldots+t_n=2n$ es $t_1=t_2=\ldots=t_n=n$.
- Se cumple que $s_n$ es impar. Para probarlo, observamos que si tenemos una solución de $t_1+t_2+\ldots+t_n=0$, entonces podemos asociarle otra intercambiando las variables que son $0$ por $2$ y viceversa mientras dejamos las que son $1$ sin cambiar. Por tanto, todas las soluciones tienen su pareja excepto una: la solución $t_1=t_2=\ldots=t_n=1$.
- Se cumple que $s_{2n-k}=s_k$. Esto se demuestra teniendo en cuenta que una solución de $t_1+t_2+\ldots+t_n=k$ se transforma en una solución de $t_1+t_2+\ldots+t_n=2n-k$ como en el punto anterior cambiando los ceros por doses y los doses por ceros.
Una vez visto esto, ya sabemos que hay siempre al menos tres términos con coeficiente impar. Vamos a probar ahora que si $n=2^m$, entonces estos tres son los únicos. Para ello usaremos inducción sobre $m$; si $m=1$ o $m=2$ el resultado está claro. Para $m\gt 2$, tenemos que cada solución de $t_1+t_2+\ldots+t_n=k$ con $0\lt k\lt n$ está emparejada con otra solución: la que resulta de cambiar los $2^{m-1}$ primeras variables en bloque por las $2^{m-1}$ últimas variables. Las únicas soluciones que están emparejadas con sigo mismas son las que tienen las primeras $n$ variables iguales que las $n$ últimas (es decir, $t_i=t_{i+\frac{n}{2}}$ para todo $i\in\{1,\ldots,\frac{n}{2}$), pero entonces $k$ tiene que ser par y los primeros $2^{m-1}$ términos son una solución de la ecuación $t_1+t_2+\ldots+t_{n/2}=\frac{k}{2}$. La hipótesis de inducción nos dice que el número de soluciones es par, luego tenemos el resultado par que queríamos probar.
Queda por ver que si $n$ no es una potencia de $2$, entonces hay algún coeficiente impar para terminar con todos los casos. Expresemos en este caso $n=a2^m$ para cierto entero impar $a\geq 3$ y veamos que la ecuación $t_1+t_2+\ldots+t_n=k$ tiene un número impar de soluciones para $k=2^m$. Para ello, descomponemos las variables $t_1,\ldots,t_n$ en $a$ grupos de $2^m$ variables consecutivas. Para cada solución, podemos rotar cíclicamente las variables en todos los grupos simultáneamente. Mediante este proceso, podemos agrupar las soluciones en grupos de $2^h$ soluciones con $h\leq m$, excepto si la solución es constante en cada grupo de variables. Esto sólo puede ocurrir si todas las variables son $1$ en uno de los grupos y $0$ en los otros grupos. Como hay un número impar de grupos, esto último nos da un número impar de soluciones y hemos probado lo que queríamos.
En resumen, la solución al problema son las potencias de $2$.
Nota. La solución está inspirada por la versión combinatoria del binomio de Newton.
Informar de error en enunciado Informar de procedencia del problema
Sesión 2 — 22 de enero de 2021 (mañana)
- Si una de las poligonales tiene vértices $M_1,M_2,M_3,M_4$ y la otra $M_5,M_6,M_7,M_8$ (en este orden), entonces es que los maestros pares $M_2,M_4,M_6,M_8$ (y también los impares $M_1,M_3,M_5,M_7$) se han enfrentado todos con todos en los primeros cinco días.
- Si hay sólo una poligonal de vértices $M_1,M_2,\ldots,M_8$ (en este orden), también ocurre que los pares (y los impares) se han enfrentado todos con todos en los primeros cinco días.
Informar de error en enunciado Informar de procedencia del problema
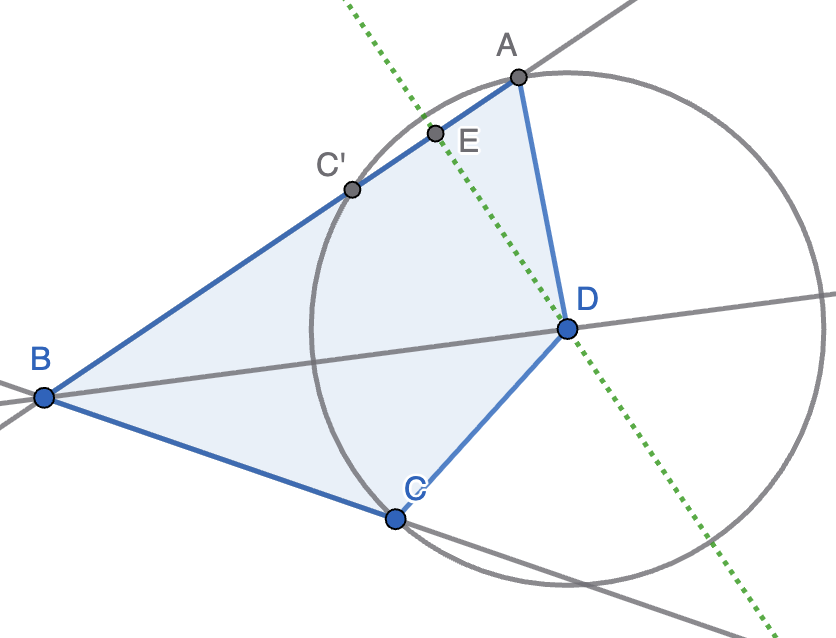
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Es fácil darse cuenta también de que la función idénticamente nula y la función identidad son soluciones de la ecuación. Sin embargo, el problema es que para algunos valores de $y$ puede ser $f(y)=y$ y para otros ser $f(y)=0$. Para ver que esto no ocurre, supongamos que $a\neq 0$ es tal que $f(a)=0$. Tomando $y=a$ en la ecuación, tenemos que el miembro de la derecha es igual a $f(xf(a)+a)=f(0+a)=f(a)=0$ y el de la izquierda igual a $f(ax)$. Deducimos que $f(ax)=0$ para todo $x\in\mathbb{R}$, lo que nos lleva a que es idénticamente nula y hemos terminado.
Informar de error en enunciado Informar de procedencia del problema