Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2764 problemas y 1057 soluciones.
IV Olimpiada Matemática Española (fase andaluza) — 2022
Sesión 1 — 5 de marzo de 2022
Problema 645
Determina todas las funciones $f:\mathbb{N}_0\to\mathbb{N}_0$, siendo $\mathbb{N}_0=\{0, 1, 2, 3,\ldots\}$ el conjunto de enteros no negativos, que verifican simultáneamente las siguientes dos condiciones:
- $f(n+2)-f(n) = 4n + 6$ para todo $n\in\mathbb{N}_0$.
- $f(2022)-f(2021) = 4044$.
pistasolución 1info
Pista. Observa que la función está determinada por los valores de $f(0)$ y $f(1)$
Solución. Escribimos la ecuación funcional del apartado para todos los números pares desde $n=0$ hasta $n=2k$. Obtenemos así las siguientes ecuaciones
\begin{align*}
f(2)-f(0)&=6&&=6+8\cdot 0\\
f(4)-f(2)&=14&&=6+8\cdot 1\\
f(6)-f(4)&=22&&=6+8\cdot 2\\
&\ \vdots\\
f(2k+2)-f(2k)&=8k+6&&=6+8\cdot k
\end{align*}
Sumando estas $k+1$ ecuaciones se cancelan casi todos los términos de las partes izquierdas (suma telescópica) y nos queda
\[f(2k+2)-f(0)=6(k+1)+8(0+1+\ldots+k)=6(k+1)+4k(k+1)=(2k+2)(2k+3).\]
Hacemos ahora el mismo razonamiento con las $k$ ecuaciones que se obtienen desde $n=1$ hasta $n=2k-1$, que están dadas por
\begin{align*}
f(3)-f(1)&=10&&=10+8\cdot 0\\
f(5)-f(3)&=18&&=10+8\cdot 1\\
f(7)-f(5)&=26&&=10+8\cdot 2\\
&\ \vdots\\
f(2k+1)-f(2k-1)&=8k+2&&=10+8\cdot (k-1)
\end{align*}
Sumando obtenemos que
\[f(2k+1)-f(1)=10k+8(0+1+2+\ldots+(k-1))=10k+4(k-1)k=(2k+3)2k.\]
Si llamamos $a=f(0)$ y $b=f(1)$, podemos expresar la función como
\[f(n)=\begin{cases}
n(n+1)+a&\text{si }n\text{ es par},\\
(n-1)(n+2)+b&\text{si }n\text{ es impar}.
\end{cases}\]
Observamos además que $f(n)\geq 0$ para todo $n\geq 0$ precisamente cuando $a\geq 0$ y $b\geq 0$. Calculamos finalmente $f(2022)=2022\cdot 2023+a$ y $f(2021)=2020\cdot 2022+b$, luego debe cumplirse que
\[4044=f(2022)-f(2021)=2022\cdot 2023+a-2020\cdot 2023-b\ \Leftrightarrow\ b=2+a.\]
Esto nos dice que las soluciones al problema son las funciones
\[f(n)=\begin{cases}
n(n+1)+a&\text{si }n\text{ es par},\\
(n-1)(n+2)+2+a&\text{si }n\text{ es impar},
\end{cases}\]
para todo $a\geq 0$ (se comprueba que todas ellas cumplen las condiciones).
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 646
Sea $ABC$ un triángulo isósceles, con $AB = AC$. Sea $P$ un punto cualquiera del segmento $BC$ distinto de $B$ y $C$, y sea $N$ el punto medio de $AP$. Se construye un trapecio (convexo) $M_1M_2N_2N_1$, siendo $M_1$ el punto medio de $BP$, $M_2$ el punto medio de $PC$ y $M_1N_1$ y $M_2N_2$ perpendiculares a $BC$, tales que $N$, $N_1$ y $N_2$ están alineados. Demostrar que el área del trapecio es la mitad del área del triángulo dado.
pistasolución 1info
Pista. Demuestra que $N$ es el punto medio de $N_1N_2$.
Solución. Llamemos $Q$ al punto medio de $BC$ y $M$ al pie de la perpendicular desde $N$ al lado $BC$ y llamemos $a=BC$ y $x=BP$. Pongamos también sin pérdida de generalidad que $P$ está más cerca de $B$ que de $C$, es decir, que $x\leq\frac{a}{2}$. Como $M_1$ es el punto medio de $BP$, tenemos que $BM_1=M_1P=\frac{x}{2}$. Como $N$ es el punto medio de $AP$ y los segmentos $NM$ y $AQ$ son paralelas, el teorema de Thales nos dice que $PM=MQ=\frac{1}{2}(\frac{a}{2}-x)=\frac{a}{4}-x$. También tenemos que $QM_2=QC-M_2C=\frac{a}{2}-\frac{a-x}{2}=\frac{x}{2}$ y de todo esto deducimos que
\[M_1M=M_1P+PM=\frac{a}{4}-\frac{x}{2},\qquad MM_2=MQ+QM_2=\frac{a}{4}-\frac{x}{2},\]
y por tanto $M$ es el punto medio de $M_1M_2$. El área del trapecio es la base media $MN$ (que es igual a $\frac{AQ}{2}$ por el mismo teorema de Thales anterior) por la altura $M_1M_2=\frac{a}{2}$, luego $M_1M_2N_2N_1$ tiene área $\frac{1}{2}(\frac{a\cdot AQ}{2})$, que es claramente la mitad del área de $ABC$.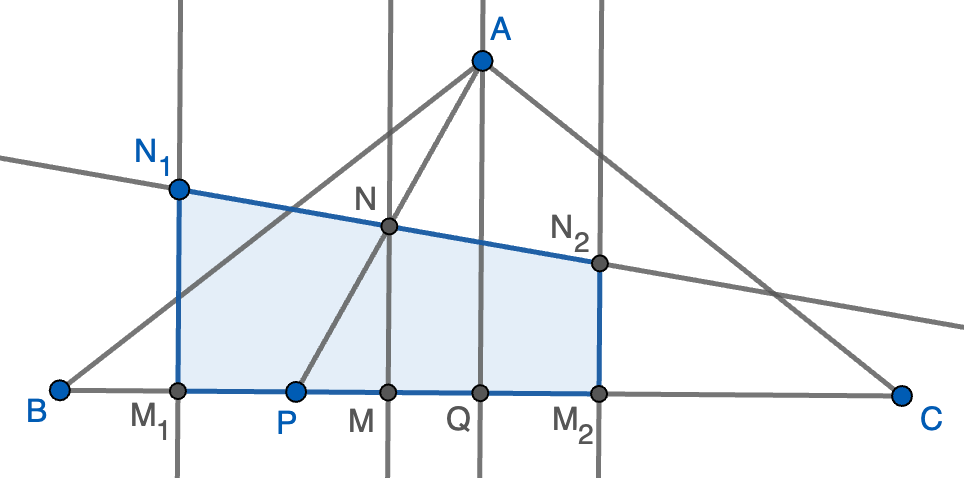

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 647
Un grupo de hombres y mujeres se sienta alrededor de una mesa circular (equidistante cada uno con sus dos vecinos). En total hay $2n$ hombres y $2n$ mujeres. Demostrar que es posible trazar un diámetro de la mesa que divida el grupo en dos partes cada una e las cuales tiene exactamente $n$ hombres y $n$ mujeres.
pistasolución 1info
Pista. ¿Qué ocurre con el número de hombres en un semicírculo de la mesa al ir rotando dicho semicírculo respecto del centro de la mesa?
Solución. Pongamos un diámetro cualquiera que deje a $2n$ personas a un lado y las otras $2n$ personas en otro y supongamos que no hay el mismo número de hombres que de mujeres en los semicírculos así determinados (si los hubiera, habríamos terminado). Rotando este diámetro respecto del centro del círculo, cada vez que sale una persona de uno de los semicírculos entra otra, cambiando el número de hombres en uno de los ellos en $-1$ (si sale un hombre y entra una mujer), $0$ (si sale una persona del mismo género que entra) o $1$ (si entra un hombre y sale una mujer. Cuando el diámetro da media vuelta al círculo, los semicírculos originales se han cambiado uno por el otro, luego, si había $k\gt n$ hombres en uno de ellos, después de la media vuelta hay $2n-k\lt n$ hombres. Como el número de hombres en este semicírculo va variando de uno en uno, necesariamente habrá un diámetro intermedio en el que exactamente haya $n$ hombres en dicho semicírculo (y, por tanto, $2n-n=n$ mujeres) y lo mismo ocurre en el otro semicírculo.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 648
Un número natural $n\lt 1000$ se dice $4$-malagueño si tiene la siguiente propiedad:
Para cualquier múltiplo $N$ de $n$ con cuatro cifras, pongamos $N = \overline{abcd}$, se verifica que todas las permutaciones circulares de $N$ ($N' = \overline{bcda}$, $N'' = \overline{cdab}$, $N''' = \overline{dabc}$) también son múltiplos de $n$. Por ejemplo, $11$ es un número $4$-malagueño.
Determina todos los números $4$-malagueños.
pistasolución 1info
Pista. Observa que $10N-N'=9999a$ es múltiplo de $n$.
Solución. Sea $n$ un número $n$-malagueño. Como $n\lt 1000$, necesariamente $n$ tiene un múltiplo de cuatro dígitos $N=\overline{abcd}$ cuyo primer dígito es $a=1$. Observando que
\[N'=10N+a-10000a=10N-9999\]
y que tanto $N$ como $N'$ son múltiplos de $n$, también debe serlo $9999$. Esto nos dice que todo número $4$-malagueño debe ser un divisor de $9999=3^2\cdot 11\cdot 101$ menor que $1000$, lo que nos da las únicas posibilidades
\[n\in\{1,3,9,11,33,99,101,303,909\}.\]
Ahora bien, si $\overline{abcd}$ es múltiplo de $3$, $9$, $11$ o $101$, cualquier permutación circular también lo es (¿por qué?), luego todos los anteriores son números $4$-malagueños y hemos terminado.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre