Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
LIX Olimpiada Matemática Española (fase local) — 2023
Sesión 1 — 20 de enero de 2023 (mañana)
Como $2^{11}=2048\gt 2023$, se tiene que ninguno de los números se escribe con más de $10$ factores primos (posiblemente repetidos). Vamos a colorear los números con $11$ colores de forma que dos números tienen el mismo número solo si tienen el mismo número de factores primos. Entonces, si $a$ es múltiplo de $b$ distinto de $b$, es porque existe un número $1\lt q\leq 2023$ tal que $a=bq$, luego $a$ y $b$ tienen distinto número de factores $a$ tiene los factores de $b$ más los factores de $q$, luego distinto color.
Informar de error en enunciado Informar de procedencia del problema
Vamos a ver que, por el contrario, María sí que puede llegar a su objetivo en cualquier otro caso. Para ello, vamos a analizar varios casos particulares:
- Si $n=3$, entonces podemos hacer las siguientes transformaciones: \[(1,2,3)\rightarrow(2,3,3)\rightarrow (3,4,3)\rightarrow (4,4,4).\]
- Si $n=4$, entonces podemos hacer las siguientes transformaciones: \[(1,2,3,4)\rightarrow(2,3,3,4)\rightarrow (3,4,3,4)\rightarrow (4,4,4,4).\]
- Si $n=5$, entonces podemos hacer las siguientes transformaciones: \[(1,2,3,4,5)\rightarrow(2,3,3,4,5)\rightarrow (3,4,3,4,5)\rightarrow (4,4,4,4,5)\rightarrow (5,5,4,4,5)\rightarrow(5,5,5,5,5).\]
Informar de error en enunciado Informar de procedencia del problema
- Probar que si una terna de números positivos $(a,b,c)$ verifica el sistema de ecuaciones \[\left\{\begin{array}{l}a^2+a=b^2,\\b^2+b=c^2,\\c^2+c=a^2,\end{array}\right.\] entonces $(a-b)(b-c)(c-a)=1$.
- Supongamos que $A_1A_2\ldots A_9$ es un eneágono regular tal que \[A_1A_4=1,\qquad A_1A_2=a,\qquad A_1A_3=b,\qquad A_1A_5=c.\] Probar que la terna $(a,b,-c)$ cumple el sistema del apartado anterior.
El apartado (b) es bastante estándar a partir del teorema de Ptolomeo para cuadriláteros cíclicos aplicado a cuadriláteros con vértices cuatro de los vértices del eneágono. Observemos que tenemos que probar tres relaciones: (1) $a^2+a=b^2$, (2) $b^2+b=c^2$ y (3) $c^2-c=a^2$ (hemos cambiado $c$ por $-c$ en las ecuaciones del sistema del apartado a). La primera de ellas se sigue de aplicar Ptolomeo al cuadrilátero $A_1A_2A_3A_4$, la segunda al cuadrilátero $A_1A_4A_6A_8$ y la tercera al cuadrilátero $A_1A_4A_5A_9$, como se indica en la figura (los segmentos verdes son iguales a $a$, los rojos a $b$, los azules a $1$ y los amarillos a $c$).
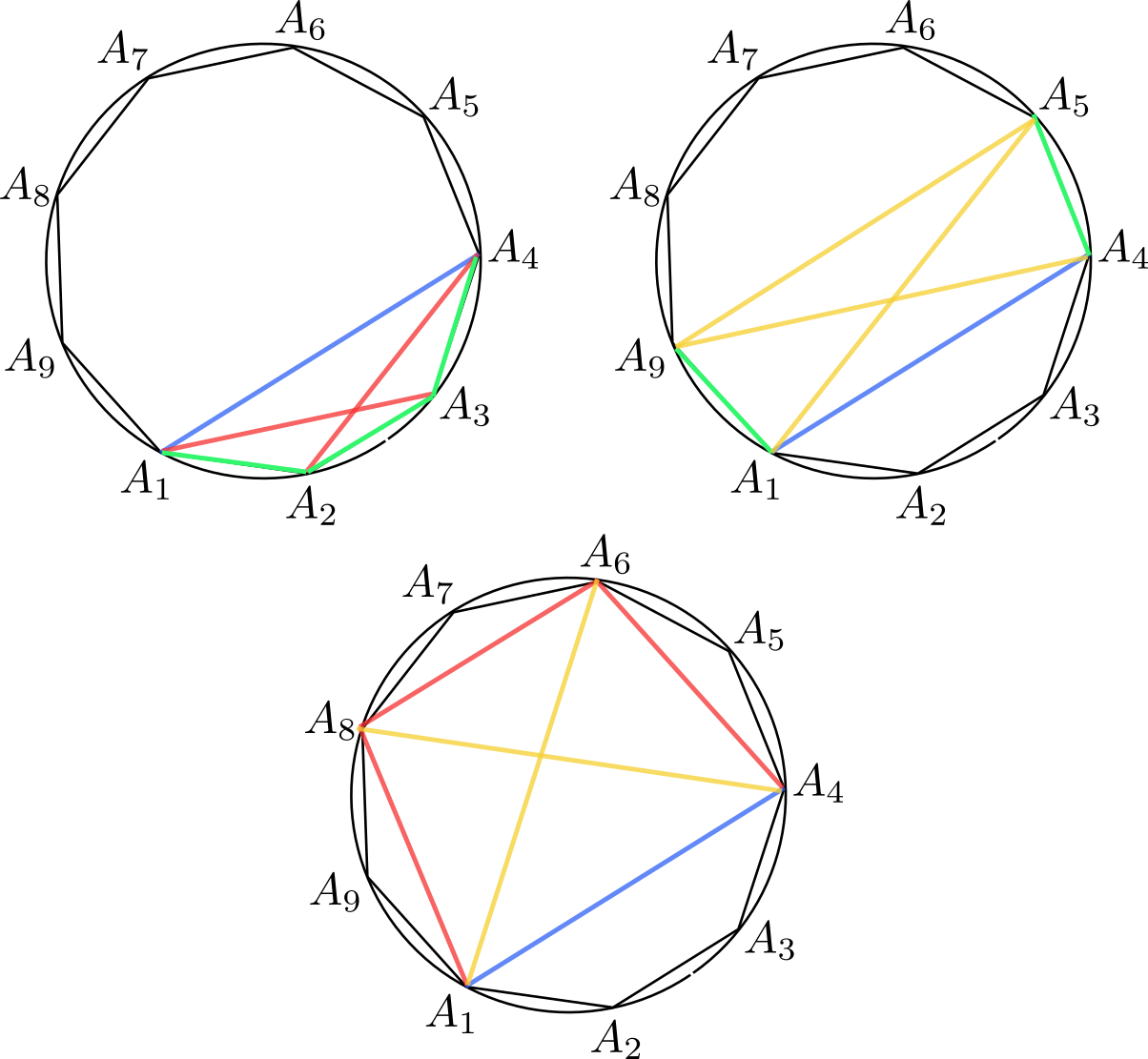
Informar de error en enunciado Informar de procedencia del problema
Sesión 2 — 20 de enero de 2023 (tarde)
Informar de error en enunciado Informar de procedencia del problema
Nota. El proceso de la demostración es, de forma encubierta, una inducción completa sobre el número de términos involucrado en la operación, para obtener una fórmula que nos permita calcular el término general, empezando con el caso base de dos términos.
Por otro lado, lo que hemos demostrado y hemos usado realmente es que la operación del enunciado es asociativa y conmutativa, con lo que el resultado no depende de cualquier posible reordenación de los elementos.
Informar de error en enunciado Informar de procedencia del problema
- Si $a=1$, entonces $7^b=c^2+2$, luego $c$ es un número impar. Módulo $8$, el miembro de la izquierda es congruente con $1$ o con $7$, mientras que el de la derecha es congruente con $3$, luego no puede haber solución en este caso.
- Si $a=2$, entonces $7^b=c^2$, luego $b$ es par y $c$ una potencia de $7$.
- Si $a\geq 3$, entonces tenemos que $7^b\equiv c^2+4\ (\text{mod }8)$. Esto es imposible ya que el miembro de la izquierda es congruente con $1$ o $7$ y el de la izquierda es congruente con $5$ ya que $c$ es impar.
Obtenemos que las soluciones son las de la forma $(a,b,c)=(2,2k,7^k)$ para cierto entero $k\geq 1$.
Informar de error en enunciado Informar de procedencia del problema
Sesión 3 — 21 de enero de 2023 (mañana)
En el caso base $n=2$, el resultado es muy fácil de ver porque al colocar las fichas $1\times 2$ y $2\times 1$ en el tablero $2\times 3$, la de tamaño $2\times 1$ debe ir pegada a uno de los lados de forma que quepa la de tamaño $1\times 2$. Esto deja un espacio (horizontal) $1\times 2$ donde deben colocarse las dos fichas $1\times 1$.
Supongamos entonces que el resultado es cierto para un tablero $(n-1)\times n$, $n\geq 3$, y vamos a probarlo para un tablero $n\times(n+1)$. La idea es similar al caso $n=2$ ya que la ficha $n\times 1$ ocupa una columna entera pero, si esta columna no es la última o la primera, entonces no deja espacio para la ficha $1\times n$. A su vez, si la ficha $1\times n$ no se coloca en la primera fila o en la última, entonces no deja espacio para la ficha $(n-1)\times 1$. Por tanto, al poner las fichas $n\times 1$ y $1\times n$, el espacio restante debe ser un subtablero rectangular $(n-1)\times n$, en el que las fichas de tamaño $1\times 1$ deben estar juntas por la hipótesis de inducción.
Nota. Problema adicional: ¿de cuántas formas distintas se pueden colocar las $2n$ fichas en las condiciones del enunciado? ¡Usa también la inducción!
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema