Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
V Olimpiada Matemática Española (fase andaluza) — 2023
Sesión 1 — 18 de febrero de 2023
Supongamos ahora que uno de los dos números es impar y vamos a ver que es imposible la coloración en este caso. Razonando por reducción al absurdo, nos damos cuenta de que en uno de los lados de longitud impar hay un número impar de lados coloreados de uno de los colores y que este color no aparece más en ningún otro lado del rectángulo $m\times n$. Como el número total de lados pintados de ese color es $mn$, uno por cada pieza cuadrada, y este número es par, debe haber necesariamente una cantidad impar de lados impares pintados en el interior del rectángulo. Esto es una contradicción ya que los lados pintados de un color que son interiores deben estar en número par pues los lados que se pegan deben ser del mismo color.
Falta por comprobar si se puede hacer la coloración cuando tanto $m$ como $n$ son pares. La imagen de la derecha nos muestra un patrón que podemos usar para colorear cualquier rectángulo $m\times 2$ ($m$ par) como nos pide el enunciado y la imagen de la derecha nos muestra un patrón para colorear cualquier rectángulo $m\times 2$ ($m$ par) pero ahora de forma que los lados de la derecha y la izquierda tengan el mismo color. Por lo tanto, adjuntando rectángulos $m\times 2$ del tipo de la izquierda a la derecha del patrón de la derecha, obtenemos coloraciones de cualquier rectángulo $m\times n$ con $m$ y $n$ pares.
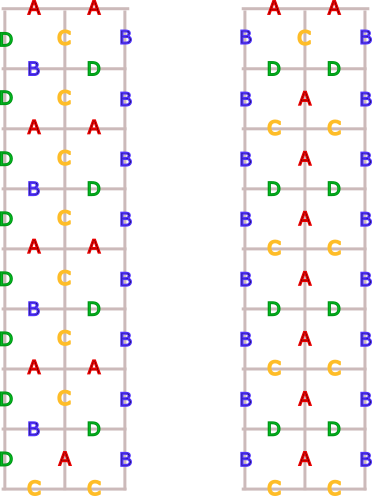
Nota. Este mismo problema apareció en la All-Soviet Union Mathematical Competition de 1984.
Informar de error en enunciado Informar de procedencia del problema
- Si $pqr\equiv 0\ (\text{mod }4)$, entonces es porque alguno de los números es par. Como son primos, necesariamente dos de ellos son iguales a dos y el tercero, por tanto, igual a $2019$. Como $2019$ no es primo (es múltiplo de $3$), deducimos que este caso no da ninguna solución.
- Si $pqr\equiv 3\ (\text{mod }4)$, entonces los tres primos son congruentes con $1$, $1$ y $3$ o bien con $3$, $3$ y $3$ (en algún orden). En cualquier caso, obtenemos que $p+q+r\equiv 1\ (\text{mod }4)$. Esto contradice el hecho de que $p+q+r=2023\equiv 3\ (\text{mod }4)$, luego tampoco obtenemos soluciones en este caso.
Deducimos que no hay primos en las condiciones del enunciado.
Nota. La misma demostración del segundo caso muestra que no hay enteros impares cumpliendo la condición del enunciado (no tienen por qué ser primos ni positivos).
Informar de error en enunciado Informar de procedencia del problema
- Supongamos en primer lugar que $f(0)=\frac{1}{2}$ y vamos a demostrar que $f(n)=\frac{1}{2}$ para todo $n\in\mathbb{N}_0$, función que claramente es solución del problema. Haciendo $m=0$ y $n=1$ en la ecuación, obtenemos que $f(1)=f(1)^2+\frac{1}{4}$, ecuación de segundo grado que tiene por única solución $f(1)=\frac{1}{2}$. Esto nos da los casos base necesarios para probar por inducción que $f(2^m)=\frac{1}{2}$ para todo $m\in\mathbb{N}$. Si $m=2k$ es par, entonces \[f(2^m)=f((2^k)^2+0^2)=f(2^k)^2+f(0)^2=\tfrac{1}{4}+\tfrac{1}{4}=\tfrac{1}{2}.\] Si $m=2k+1$ es impar, entonces \[f(2^m)=f((2^k)^2+(2^k)^2)=f(2^k)^2+f(2^k)^2=\tfrac{1}{4}+\tfrac{1}{4}=\tfrac{1}{2}.\] Ahora bien, cualquier $n\in\mathbb{N}_0$ se puede encajar entre dos potencias consecutivas de $2$ de forma que existe $m\in\mathbb{N}_0$ tal que $2^m\leq n\leq 2^{m+1}$. El hecho de que $f$ sea creciente asegura que $\frac{1}{2}=f(2^m)\leq f(n)\leq f(2^{n+1})=\frac{1}{2}$, de donde deducimos que $f(n)=\frac{1}{2}$ para todo $n\in\mathbb{N}_0$.
- Supongamos ahora que $f(0)=0$. Haciendo $m=0$ y $n=1$ en la ecuación funcional, llegamos a que $f(1)=f(1)^2$, lo que nos da $f(1)=0$ o bien $f(1)=1$. Si $f(1)=0$, podemos probar por inducción igual que en el caso anterior que $f(2^m)=0$ para todo $m\in\mathbb{N}$, lo que nos lleva a que $f(n)=0$ para todo $n\in\mathbb{N}$ por la monotonía, y esta también es solución de la ecuación. Si, por el contrario, suponemos que $f(1)=1$, la misma idea de nuevo nos dice que $f(2^m)=2^m$ para todo $m\in\mathbb{N}_0$, pero ahora la monotonía no nos ayuda a conocer el valor del resto de naturales que no son potencia de $2$. Observamos que $f(5)=f(2^2+1^2)=f(2)^2+f(1)^2=5$ y $f(25)=f(5)^2+f(0)^2=25$, con lo que \[25=f(25)=f(3^2+4^2)=f(3)^2+f(4)^2=f(3)^2+16,\] de donde obtenemos que $f(3)=3$. Como $100=6^2+8^2=10^2+0^2$, también tenemos que \[f(6)^2+64=f(6)^2+f(8)^2=f(10)^2+f(0)^2=f(3^2+1^2)^2=(f(3)^2+f(1)^2)^2=100,\] de donde deducimos que $f(6)=6$. De la igualdad $7^2+1^2=5^2+5^2$ se deduce que $f(7)=7$ y de $9=3^2+0^2$ que $f(9)=9$. Vamos a probar finalmente por inducción sobre $n$ que $f(n)=n$ para todo $n\in\mathbb{N}$. Sabemos que se cumple para $n\leq 9$ por los comentarios anteriores, casos que nos servirán como base para la inducción. Si $n=2k\geq 10$ es par, entonces podemos considerar la identidad $(2k)^2+(k-5)^2=(2k-4)^2+(k+3)^2$ para escribir \[f(2k)^2+f(k-5)^2=f(2k-4)^2+f(k+3)^2.\] Como los números $k-5$, $2k-4$ y $k+3$ son no negativos y menores que $n$, podemos usar la hipótesis de inducción y deducir de lo anterior que \[f(2k)^2+(k-5)^2=(2k-4)^2+(k+3)^2\ \Longleftrightarrow\ f(2k)^2=4k^2,\] luego obtenemos que $f(n)=n$. Si $n=2k+1\geq 11$ es impar, entonces podemos usar el mismo argumento teniendo en cuenta la identidad $(2k+1)^2+(k-2)^2=(2k-1)^2+(k+2)^2$.
Informar de error en enunciado Informar de procedencia del problema
- Si en $V$ sólo hay un polígono pequeño $Q$, entonces $Q$ también es un $n$-gono. Como $P$ se descompone en más de un polígono, entonces $Q$ tiene que tener otro vértice $V'$ en un lado de $P$ adyacente a $V$. En el vértice $V'$ deben confluir más polígonos pequeños.
- Si $n\geq 7$, entonces es imposible que esto ocurra porque el ángulo interior del $n$-gono es $180(1-\frac{2}{n})$, que deja un ángulo restante en $V'$ de $\frac{360}{n}\lt 60$, en el que no caben más polígonos regulares ya que el ángulo más pequeño es el del triángulo ($60$).
- Si $n=5$, un pentágono deja un ángulo restante en $V'$ de $\frac{360}{5}=72$. Este tampoco se pude cubrir con ángulos interiores de otros polígonos regulares ya que sólo caben triángulos (y 60 no divide a 72).
- Si $n$ es igual a $3$, $4$ o $6$, entonces sí se puede hacer el recubrimiento, como mostramos más adelante.
- Si en $V$ hay más de un polígono, por el mismo motivo expuesto en el caso anterior, no puede haber $n$-gonos con $n\geq 6$. Además, si colocamos más de dos polígonos en $V$, entonces obtendríamos un ángulo de 180 o más en $V$. Tenemos entonces, las siguientes tres posibilidades para no pasarnos de $180$ en $V$:
- Dos triángulos: nos lleva a un ángulo interior en $V$ de $120$, luego $n=6$. El hexágono sí puede recubrirse como veremos más adelante.
- Un triángulo y un cuadrado: lleva a un ángulo interior en $V$ de $150$, que se corresponde con $n=12$. El dodecácgono sí puede recubrirse, como veremos más adelante.
- Un triángulo y un pentágono: lleva a un ángulo interior en $V$ de $168$, que no es de la forma $180(1-\frac{2}{n})$ ya que obtendríamos $n=\frac{15}{2}\not\in\mathbb{N}$.
Resta por ver que el triángulo, el cuadrado, el hexágono y el dodecágono pueden recubrirse con polígonos regulares, pero esto es fácil a partir de la discusión anterior, lo que nos da las siguientes figuras:
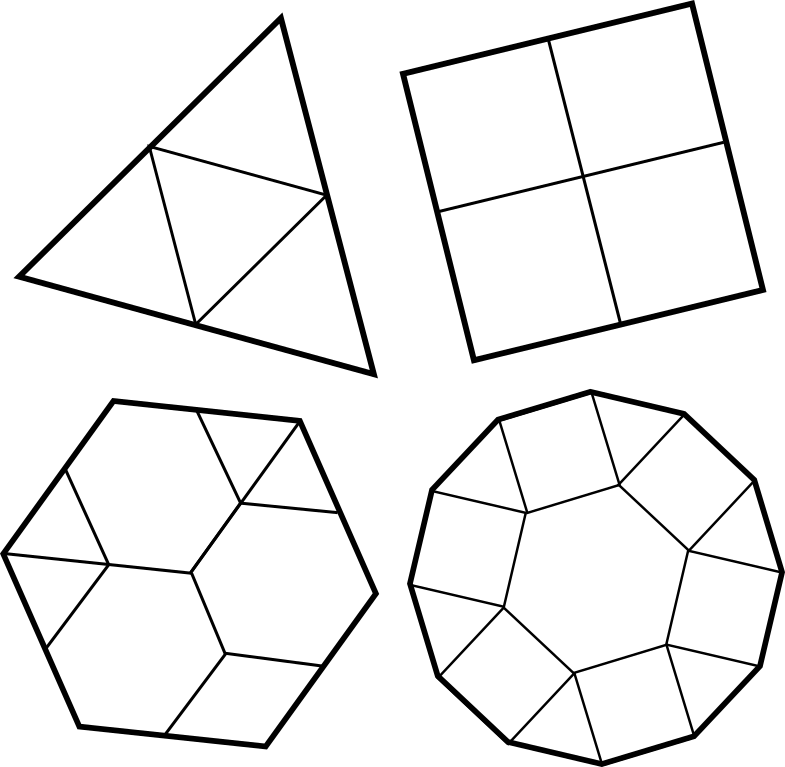
Nota. La forma de subdividir cada polígono obviamente no es única (por ejemplo, cada una de las piezas de los ejemplos dados puede volver a subdividirse a su vez).
Informar de error en enunciado Informar de procedencia del problema