Sea $ABCD$ un paralelogramo y sea $M$ un punto en la diagonal $BD$ que cumple $MD=2BM$. Las rectas $AM$ y $BC$ se cortan en un punto $N$. ¿Cuál es el
cociente entre el área del triángulo $MND$ y el área del paralelogramo $ABCD$?
pistasolución 1info
Pista. Observa que $N$ es el punto medio de $BC$.
Solución. Los triángulos $AMD$ y $BMN$ son semejantes (están en posición de Thales ya que $AD$ y $BC$ son paralelas) y la razón de semejanza es $\frac{1}{2}$ ya que el enunciado nos dice que $MD=2BM$. Por lo tanto, $BN=\frac{1}{2}AD=\frac{1}{2}BC$ y tenemos que $N$ es el punto medio de $BC$. De esta forma, el área $BCD$, que es la mitad de la del paralelogramo, es a su vez el doble del área de $DBN$ (por tener la misma base y altura doble). Por otro lado, el área de $DMN$ es el doble de la de $BMN$ (ya que tiene doble base e igual altura). Todo esto nos dice que
\begin{align*}
\mathrm{Area}(ABCD)&=2\,\mathrm{Area}(BCD)=4\,\mathrm{Area}(BND)\\
&=4(\mathrm{Area}(MND)+\mathrm{Area}(MNB))\\
&=4(\mathrm{Area}(MND)+\tfrac{1}{2}\mathrm{Area}(MND))=6\,\mathrm{Area}(MND).
\end{align*}
Deducimos así que
\[\frac{\mathrm{Area}(MND)}{\mathrm{Area}(ABCD)}=\frac{1}{6}.\]
Sea $q(x)$ un polinomio de grado $2023$ que cumple que $q(n)=\frac{1}{n}$ para todo entero $n=1,2,\ldots,2024$. Hallar el valor de $q(2025)$.
pistasolución 1info
Pista. Considera el polinomio $p(x)=xq(x)-1$.
Solución. Consideremos el polinomio $p(x)=x\,q(x)-1$, que tiene grado $2024$ y cumple que $p(n)=0$ para $n=1,2,\ldots, 2024$. En particular, como conocemos sus $2024$ raíces, podremos escribir
\[p(x)=x\,q(x)-1=a(x-1)(x-2)(x-3)\cdots(x-2024).\]
Evaluando esta igualdad en $x=0$, llegamos a que $p(0)=-1=2024! a$, luego obtenemos que $a=\frac{-1}{2024!}$ y tenemos ya completamente determinado $p(x)$. Ahora solamente hay que evaluar en $x=2025$, obteniendo
\[p(2025)=2025\,q(2025)-1=\frac{-(2025-1)(2025-2)(2025-3)\cdots(2025-2024)}{2024!}=-1.\]
Despejamos fácilmente $q(2025)=0$ y hemos terminado.
Dividimos cada lado de un triángulo equilátero en $n$ partes iguales,
uniendo cada vértice de la división con el vértice opuesto. Determina el número de puntos de intersección interiores al triángulo determinados por estos segmentos en los siguientes casos:
- $n$ es un número primo impar.
- $n=2p^2$, donde $p$ es un número primo impar.
pistasolución 1info
Pista. Utiliza el teorema de Ceva para saber cuándo tres de los segmentos trazados se cortan en un único punto.
Solución. Supongamos que el triángulo $ABC$ tiene lado $n$ y que trazamos tres segmentos, uno desde cada vértice que lo une con un punto del lado opuesto, de forma que el punto sobre el lado $AB$ está a distancia $a$ de $A$, el punto sobre el lado $BC$ está a distancia $b$ de $B$ y el punto sobre el lado $CA$ está a distancia $c$ de $C$. En principio los tres segmentos se cortan en tres puntos distintos pero podrían cortarse en uno solo. Por el teorema de Ceva, esto último ocurre si y sólo si
\[\frac{abc}{(n-a)(n-b)(n-c)}=1,\]
lo que puede reescribirse como
\[2abc=n^3-(a+b+c)n^2+(ab+bc+ca)n.\qquad (\star)\]
- En el caso en que $n$ es un primo impar $p$, para que se cumpla $(\star)$, el producto $abc$ tiene que ser múltiplo de de $p$, luego uno de los tres números $a,b,c$ tiene que ser múltiplo de $p$. Esto es imposible ya que $1\leq a,b,c\leq n-1=p-1$, luego no hay tres segmentos que se corten en el mismo punto. Entonces, como cada uno de los $3(n-1)$ segmentos corta a $2(n-1)$ y los puntos de corte son distintos, tendremos un total de $6(n-1)^2$ puntos de intersección contados dos veces. Por lo tanto, el número que nos piden es $3(n-1)^2$ en este caso.
- Si $n=2p^2$, con $p$ primo impar, para que se cumpla $(\star)$ el producto $abc$ es múltiplo de $p^2$. Distinguimos entonces subcasos:
- Supongamos que ninguno de los tres números $a,b,c$ es múltiplo de $p^2$. Entonces, hay dos de ellos que son múltiplos de $p$, pongamos $a$ y $b$. El miembro de la derecha de $(\star)$ es múltiplo de $p^3$, luego el de la izquierda tiene que serlo. Por lo tanto, $c$ también es múltiplo de $p$ y ahora el miembro de la derecha es múltiplo de $p^4$, lo que nos lleva a que uno de los números $a,b,c$ sea múltiplo de $p^2$. Esto va en contra de nuestra suposición, luego no hay soluciones en este subcaso.
- Si $a=p^2$ y $b,c\neq p^2$, entonces $n-a=p^2$ y la ecuación $(\star)$ queda tras simplificar como $b+c=2p^2$, luego tenemos $2p^2-2$ soluciones de dicha ecuación ($b$ puede ser cualquier número entre $1$ y $2p^2-1$ distinto de $p^2$). Análogamente, si $b=p^2$ y $a,c\neq p^2$ o bien $c=p^2$ y $a,b\neq p^2$, tenemos $2p^2-2$ soluciones en cada caso. Finalmente está la solución $a=b=c=p^2$, luego tenemos $6p^2-5=3n-5$ soluciones de $(\star)$ en este caso.
Tenemos así que de los $3(n-1)^2$ puntos de corte que hay tenemos que quitar $2(3n-5)$ ya que cada una de las $3n-5$ soluciones de $(\star)$ hace que tres de los $3(n-1)^2$ puntos totales coincidan en uno solo. Tenemos entonces $3(n-1)^2-2(3n-5)=3n^2-12n+13$ puntos de corte en este caso.
Determinar el menor entero positivo $n$ que tiene al menos $4$ divisores diferentes $a,b,c,d$, todos ellos distintos de $1$ y de $n$, de forma que
\[a+b+c+d=1001.\]
pistasolución 1info
Pista. Observa que los cuatro divisores son, a lo sumo, $\frac{n}{2},\frac{n}{3},\frac{n}{4},\frac{n}{5}$ por ser distintos.
Solución. Observamos que el mayor divisor de $n$ es menor o igual que $\frac{n}{2}$, el segundo mayor divisor será menor o igual que $\frac{n}{3}$, el tercero menor o igual que $\frac{n}{4}$ y el cuarto menor o igual que $\frac{n}{5}$. Por lo tanto, se cumple que
\[1001=a+b+c+d\leq \frac{n}{2}+\frac{n}{3}+\frac{n}{4}+\frac{n}{5}=\frac{77}{60}n\ \Longleftrightarrow\ n\geq 780.\]
Buscamos, por tanto, un número mayor o igual que $780$. Como $780$ resulta ser divisible entre $2,3,4,5$, la desigualdad anterior se convierte en una igualdad la igualdad si tomamos
\[a=\frac{780}{2}=390,\qquad b=\frac{780}{3}=260,\qquad c=\frac{780}{4}=195,\qquad d=\frac{780}{5}=156,\] lo que demuestra que $n=780$ es el número que buscamos.
Sea $ABCD$ un cuadrilátero convexo tal que las rectas $AB$ y $CD$ se cortan en un punto $F$ y las rectas $AD$ y $BC$ se cortan en un punto $E$. Demostrar que las circunferencias circunscritas de los triángulos $BFC$, $AFD$, $DCE$ y $ABE$ tienen un punto en común.
pistasolución 1info
Pista. Considera el punto de corte de dos de las circunferencias y demuestra que pertenece a las otras dos usando repetidamente el arco capaz (¡caza de ángulos!).
Solución. Consideremos las circunferencias circunscritas a los triángulos $ABE$ y $AFD$, que se cortarán en $A$ y en otro punto $P$. Queremos ver que este punto $P$ pertenece a las otras dos circunferencias circunscritas, para lo que vamos a usar la propiedad del arco capaz. Llamaremos $\alpha,\beta,\gamma,\delta$ a los ángulos del cuadrilátero $A,B,C,D$ por comodidad.
Como $ADPF$ es cíclico, tenemos que $\angle APD=\angle AFD=180-\alpha-\delta$ y, como $ABPE$ es cíclico, tenemos que $\angle APB=\angle AEB=180-\alpha-\beta$, luego
\[\angle DPB=\angle DPA+\angle APB=(180-\alpha-\delta)+(180-\alpha-\beta)=360-2\alpha-\beta-\delta=\gamma-\alpha,\]
donde hemos usado que $\alpha+\beta+\gamma+\delta=360$. Ahora bien, como $ADPF$ es cíclico, tenemos que $\angle DPF=180-\angle DAF=180-\alpha$, luego obtenemos que
\[\angle BPF=\angle DPF-\angle APF=(180-\alpha)-(\gamma-\alpha)=180-\gamma=\angle BCF.\]
De este modo, los dos ángulos indicados en rojo en la figura son iguales, luego $P$ está en la circunferencia circunscrita al triángulo $BFC$. Con la circunferencia $DCE$ se razona igual (sólo hay que cambiar $E$ por $F$ y $B$ y $\beta$ por $D$ y $\delta$ en el razonamiento anterior).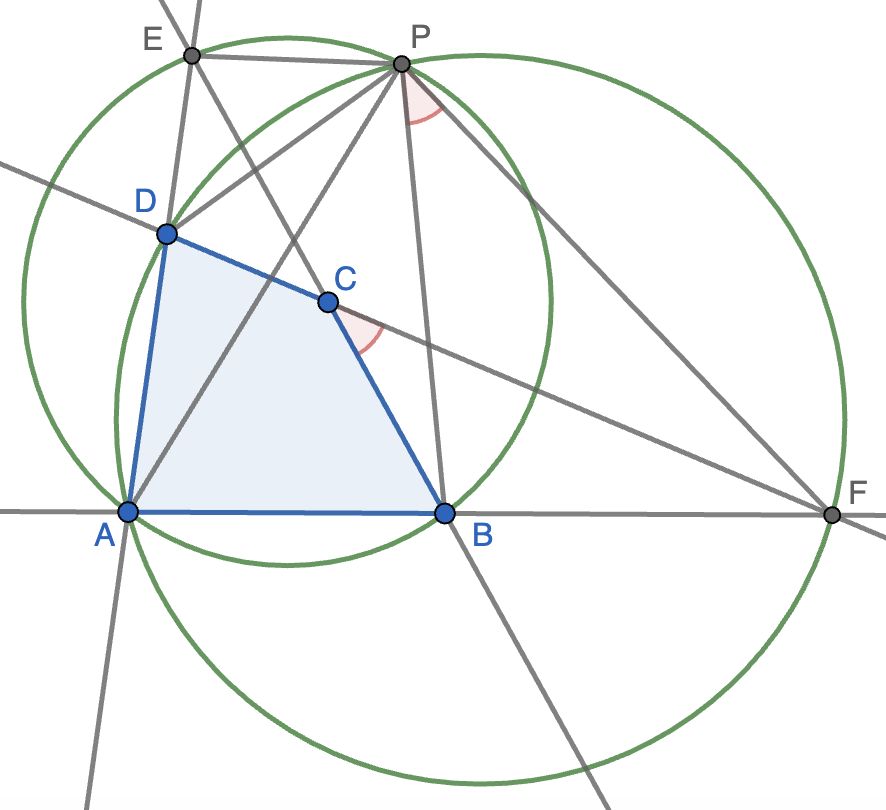
Encontrar todas las funciones $f:(0,+\infty)\to(0,+\infty)$ que cumplen que
\[f(x\,f(y))=f(xy)+x\]
para cualesquiera $x,y\gt 0$.
pistasolución 1info
Pista. Haz $x=f(z)$ en la ecuación funcional y usa la simetría de la expresión resultante.
Solución. Si hacemos $x=f(z)$ en la ecuación funcional, obtenemos que
\[f(f(z)f(y))=f(yf(z))+f(z)\stackrel{\star}{=}f(yz)+y+f(z),\]
donde en $\star$ hemos usado de nuevo la ecuación funcional. Como lo anterior es cierto para cualesquiera $y,z\gt 0$ y hay términos simétricos, intercambiando $z$ por $y$, obtenemos que \[f(yz)+y+f(z)=f(f(z)f(y))=f(zy)+z+f(y),\]
de donde $y+f(z)=z+f(y)$ para todo $y,z\gt 0$. Esto nos lleva a que $f(z)=z+a$ para cierto $a\in\mathbb{R}$. Sin embargo, la única de estas funciones que cumple la ecuación original es para $a=1$ y deducimos que $f(z)=z+1$ es la única solución.
Hallar todos los números enteros $a$ y $b$ que satisfacen la ecuación
\[a(a^2+b^2)+7=5a^2+3b^2.\]
pistasolución 1solución 2info
Pista. Resta $7$ a ambos miembros que el miembro de la derecha debe ser divisible entre $a^2+b^2$ y, por tanto también, deben serlo $2b^2-7$ y $2a^2+7$. Ahora bien, todo divisor es menor o igual que el valor absoluto del número al que divide. Otra opción es probar que no puede ser $a\geq 5$ ni $a\leq -2$ estimando mediante desigualdades la ecuación inicial.
Solución. Escribimos la ecuación como
\[a(a^2+b^2)+7=3(a^2+b^2)+2b^2\ \Leftrightarrow\ (a-3)(a^2+b^2)=2b^2-7,\]
luego $a^2+b^2$ es un divisor de $2b^2-7$. Ahora la escribimos como
\[a(a^2+b^2)+7=5(a^2+b^2)-2a^2\ \Leftrightarrow\ (5-a)(a^2+b^2)=2a^2+7,\]
luego también es divisor de $2a^2+7$. Como todo divisor positivo de un número es menor o igual que el valor absoluto de dicho número, tenemos que
\[\left\{\begin{array}{l}a^2+b^2\leq|2b^2-7|,\\a^2+b^2\leq 2a^2+7.\end{array}\right.\]
Distinguimos casos para tratar con el valor absoluto:
- Si $b=0$, entonces la ecuación original queda $a^3-5a^2+7=0$, que no tiene soluciones enteras (probamos $a=\pm 1$ y $a=\pm 7$, los divisores del término independiente).
- Si $b=\pm 1$, entonces la ecuación original queda $a^3-5a^2+a+4=0$, que tampoco tiene soluciones enteras (probamos $a=\pm 1$, $a=\pm 2$ y $a=\pm 4$).
- Si $|b|\geq 2$, entonces $2b^2-7\gt 0$, luego el sistema anterior de desigualdades nos da $a^2\leq b^2-7$ y $b^2\leq a^2+7$, lo que a su vez implica que $b^2-a^2=7$. Es fácil ver que los únicos cuadrados que se diferencian en $7$ unidades son $3^2=9$ y $4^2=16$ (a partir de $16$, cada cuadrado se diferencia del siguiente en al menos $9$ unidades). Por tanto, tenemos los candidatos a solución $a=\pm 3$ y $b=\pm 4$. Sustituyendo en la ecuación original, obtenemos que solamente $(a,b)=(3,4)$ y $(a,b)=(3,-4)$ la verifican.
Hemos probado así que $(a,b)=(3,4)$ y $(a,b)=(3,-4)$ son las únicas soluciones.
Solución. En la ecuación que nos dan podemos despejar
\[b^2=\frac{a^3-5a^2+7}{3-a}=f(a)\]
siempre que $a\neq 3$. Para $a=3$, la ecuación original queda $-11=0$, luego podemos suponer sin problema que $a\neq 3$. La función $f(a)$ tiende a $-\infty$ cuando $a\to\pm\infty$, lo que nos dice que debería haber pocos valores en los que $f(a)=b^2\gt 0$. Veamos entonces para qué enteros $a$ se cumple que $f(a)\gt 0$.
El numerador de $f(a)$ tiene grado $3$, luego la ecuación $f(a)=0$ tiene a lo sumo tres soluciones reales. Calculamos algunos valores:
\[f(-2)=-\tfrac{21}{5}\lt 0,\quad f(-1)=\tfrac{1}{4}\gt 0,\quad f(1)=\tfrac{3}{2}\gt 0,\quad f(2)=-5\lt 0,\]
\[f(0)=\tfrac{7}{3}\gt 0,\quad f(4)=9\gt 0,\quad f(5)=-\tfrac{7}{2}\lt 0.\]
Como hemos encontrado dos cambios de signo en el intervalo $(-\infty,3)$ y otro en $(3,+\infty)$, en los que $f$ es continua, el teorema de Bolzano nos garantiza entonces que en esos cambios de signo se encuentran las tres raíces del numerador de $f(x)$. En particular, tenemos que $f(a)\lt 0$ para $a\leq -2$, para $a=2$ y para $a\geq 5$, luego las únicas posibilidades son $a=\pm 1$, $a=0$ y $a=4$. Sin embargo, a la vista de los valores dados arriba, sólo $f(4)$ es un cuadrado perfecto. Concluimos de este modo que la ecuación original tiene únicamente las soluciones enteras $(a,b)=(4,\pm 3)$.
Consideramos una lista con los números $0$, $1$ y $\sqrt{3}$. De manera sucesiva, se va aplicando la siguiente operación: se escoge uno de los tres números de la lista y se le añade un múltiplo racional arbitrario de la diferencia de los otros dos. Repitiendo el proceso, ¿es posible conseguir que los tres números de la lista sean $0$, $\sqrt{3}-1$ y $\sqrt{3}+1$?
pistasolución 1info
Pista. Piensa en cada número $x+y\sqrt{3}$ como en el punto del plano de coordenadas $(x,y)$ y ahora piensa en en la operación propuesta como una operación sobre el triángulo que tiene a dichos números por vértices.
Solución. Los números que se obtienen de esta manera son siempre de la forma $x+y\sqrt{3}$ para ciertos $x,y\in\mathbb{Q}$. Vamos a identificar entonces cada número con el punto $(x,y)$ en el plano. Al sumarle a un punto un múltiplo racional de la diferencia de los otros dos, no hacemos más que mover uno de los vértices del triángulo que forman en la dirección paralela al lado opuesto (ya que la diferencia representa el vector director de la recta que forman dichos puntos en el plano). Originalmente, los tres puntos son $(0,0),(1,0),(0,1)$, que forman un triángulo de área $\frac{1}{2}$ y queremos llegar a los puntos $(0,0),(-1,1),(1,1)$, que forman un triángulo de área $1$. Por tanto, es imposible conseguir esos tres números.
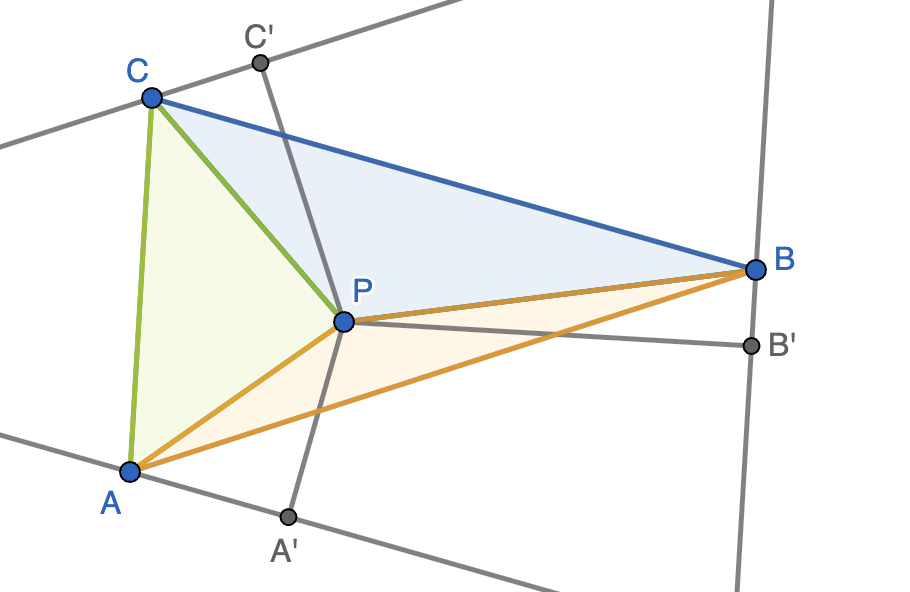
Sea $ABC$ un triángulo acutángulo cuyos lados tienen longitudes $a$, $b$ y $c$ y sea $S$ el área del triángulo. Sea $P$ un punto interior del triángulo de forma que
\[a\cdot PA+b\cdot PB+c\cdot PC=4S.\]
Demostrar que $P$ es el ortocentro del triángulo $ABC$.
pistasolución 1info
Pista. Demuestra que $a\cdot PA+b\cdot PB+c\cdot PC\geq 4S$ para cualquier punto P$ interior, para lo que puede ser útil ver los productos $a\cdot PA$, $b\cdot PB$ y $c\cdot PC$ como áreas. Luego estudia qué tiene que ocurrir para que se alcance la igualdad.
Solución. Trazamos por cada vértice del triángulo una paralela al lado opuesto y definimos los puntos $A',B',C'$ como los pies de las perpendiculares desde $P$ a estas tres rectas, como se muestra en la figura. Tenemos entonces que
\begin{align*}
\mathrm{Area}(ACPB)&=\mathrm{Area}(ABC)-\mathrm{Area}(BPC)=\tfrac{1}{2}a\cdot PA',\\
\mathrm{Area}(CBPA)&=\mathrm{Area}(ABC)-\mathrm{Area}(ABP)=\tfrac{1}{2}b\cdot PB',\\
\mathrm{Area}(BAPC)&=\mathrm{Area}(ABC)-\mathrm{Area}(CPA)=\tfrac{1}{2}c\cdot PC',
\end{align*}
ya que $PA',PB',PC'$ representan la diferencia de alturas de los triángulos cuyas áreas se restan y $a,b,c$ sus bases. Si sumamos las áreas de estos tres cuadriláteros cóncavos, obtenemos dos veces el área de $ABC$, luego esta suma nos da
\[4S=a\cdot PA'+b\cdot PB'+c\cdot PC'.\]
Sin embargo, tenemos que $PA'\leq PA$ ya que $APA'$ es un triángulo rectángulo en el que $PA'$ es un cateto y $PA$ es la hipotenusa. De la misma manera, se cumple que $PB'\leq PB$ y $PC'\leq PC$. En consecuencia,
\[4S\leq a\cdot PA+b\cdot PB+c\cdot PC\]
para cualquier punto $P$ interior al triángulo. Para que la igualdad se alcance, en los triángulos rectángulos $APA'$, $BPB'$ y $CPC'$ tiene que ser $AA'=BB'=CC'=0$, luego $PA=PA'$ es perpendicular a $BC$, $PB=PB'$ es perpendicular a $AC$ y $PC=PC'$ es perpendicular a $AB$. En definitiva, la igualdad se cumple si y sólo si $P$ es está en las tres alturas del triángulo, es decir, sólo si $P$ es el ortocentro.