Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
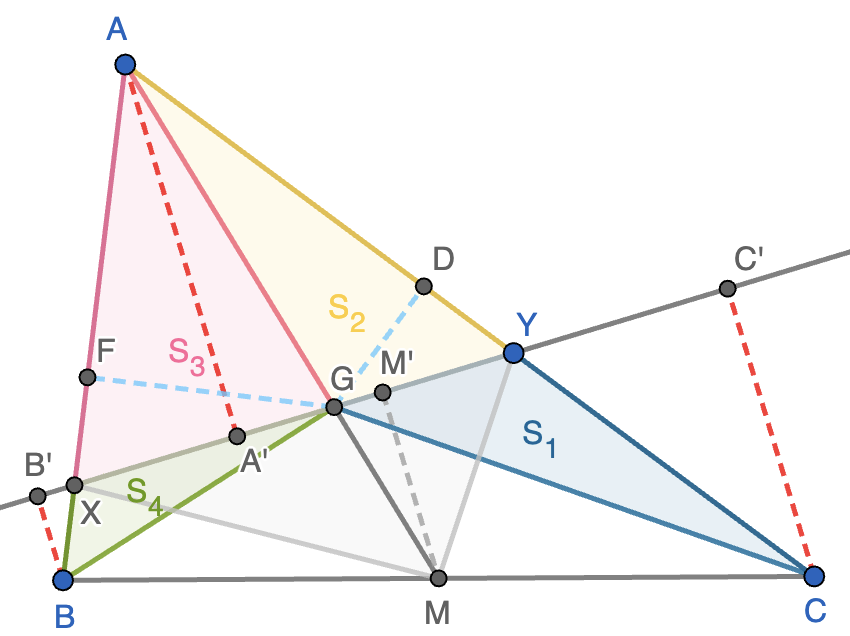
Nota. Este problema es una reformulación del problema 3 de la fase nacional de la Olimpiada Matemática Española de 1995.
Informar de error en enunciado Informar de procedencia del problema
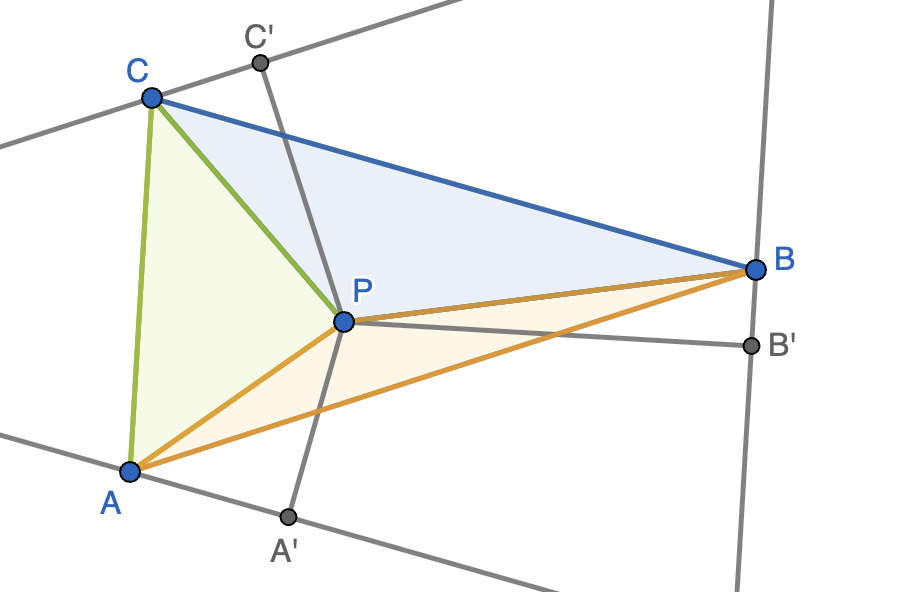
Informar de error en enunciado Informar de procedencia del problema
Como $ADPF$ es cíclico, tenemos que $\angle APD=\angle AFD=180-\alpha-\delta$ y, como $ABPE$ es cíclico, tenemos que $\angle APB=\angle AEB=180-\alpha-\beta$, luego
\[\angle DPB=\angle DPA+\angle APB=(180-\alpha-\delta)+(180-\alpha-\beta)=360-2\alpha-\beta-\delta=\gamma-\alpha,\]
donde hemos usado que $\alpha+\beta+\gamma+\delta=360$. Ahora bien, como $ADPF$ es cíclico, tenemos que $\angle DPF=180-\angle DAF=180-\alpha$, luego obtenemos que
\[\angle BPF=\angle DPF-\angle APF=(180-\alpha)-(\gamma-\alpha)=180-\gamma=\angle BCF.\]
De este modo, los dos ángulos indicados en rojo en la figura son iguales, luego $P$ está en la circunferencia circunscrita al triángulo $BFC$. Con la circunferencia $DCE$ se razona igual (sólo hay que cambiar $E$ por $F$ y $B$ y $\beta$ por $D$ y $\delta$ en el razonamiento anterior).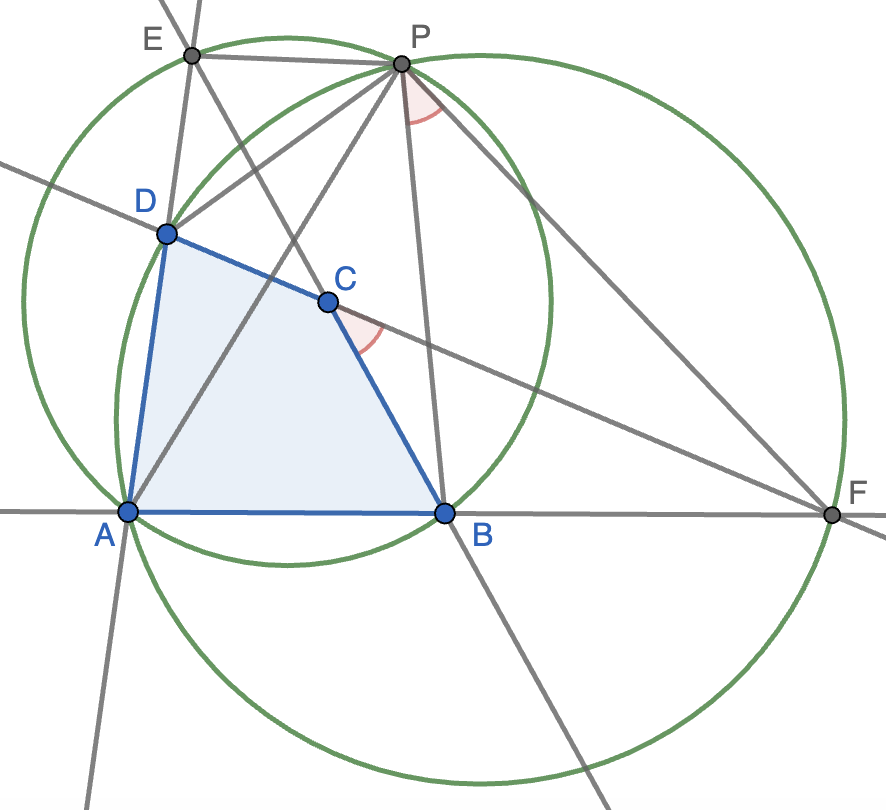
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema