Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
- Demostrar que los ángulos formados por las medianas son iguales a los del triángulo $ABC$.
- Demostrar que el triángulo cuyos lados son las medianas de $ABC$ es semejante al triángulo $ABC$.
Observamos en primer lugar que $AN=\frac{\sqrt{3}}{\sqrt{2}}$ sin más que aplicar el teorema de Pitágoras a $ABN$. También se tiene que $CM=\frac{3}{2}$ aplicando el teorema de Pitágoras a $BCM$. Por último, se tiene que $BP=\frac{\sqrt{3}}{2}$ ya que es la mitad de la diagonal del rectángulo. Por lo tanto, las tres medianas tienen longitudes $\frac{\sqrt{3}}{2},\frac{\sqrt{3}}{\sqrt{2}},\frac{3}{2}$, que son números proporcionales a $1,\sqrt{2},\sqrt{3}$ y, de esta forma, hemos respondido al apartado (b).
Dado que el baricentro $G$ corta a cada mediana en segmentos uno doble que el otro, podemos calcular $GN=\frac{1}{3}AN=\frac{1}{\sqrt{6}}$ y $GC=\frac{2}{3}CM=1$. Como también tenemos que $CN=\frac{1}{\sqrt{2}}$, podemos despejar el coseno del ángulo $\angle NGC$ utilizando el teorema del coseno en el triángulo $GCN$: \[\cos\angle CGN=\frac{GN^2+GC^2-CN^2}{2\,GN\cdot GC}=\frac{\frac{1}{6}+1-\frac{1}{2}}{2\cdot\frac{1}{\sqrt{6}}\cdot 1}=\frac{\sqrt{2}}{\sqrt{3}},\] que coincide con el coseno de $\angle ACB$. Como ambos ángulos están entre $0$ y $180$, deben ser iguales. Se razona de la misma forma que $\angle BGN=\angle BAC$ y se razona también que $\angle AGP=90^\circ=\angle ABC$ sin más que comprobar que $BG^2+AG^2=AB^2$.
Informar de error en enunciado Informar de procedencia del problema
- El radio $r_n$ de la esfera introducida en $n$-ésimo lugar.
- El volumen comprendido entre el cono y las esferas introducidas en los lugares $n$-ésimo y $(n+1)$-ésimo.
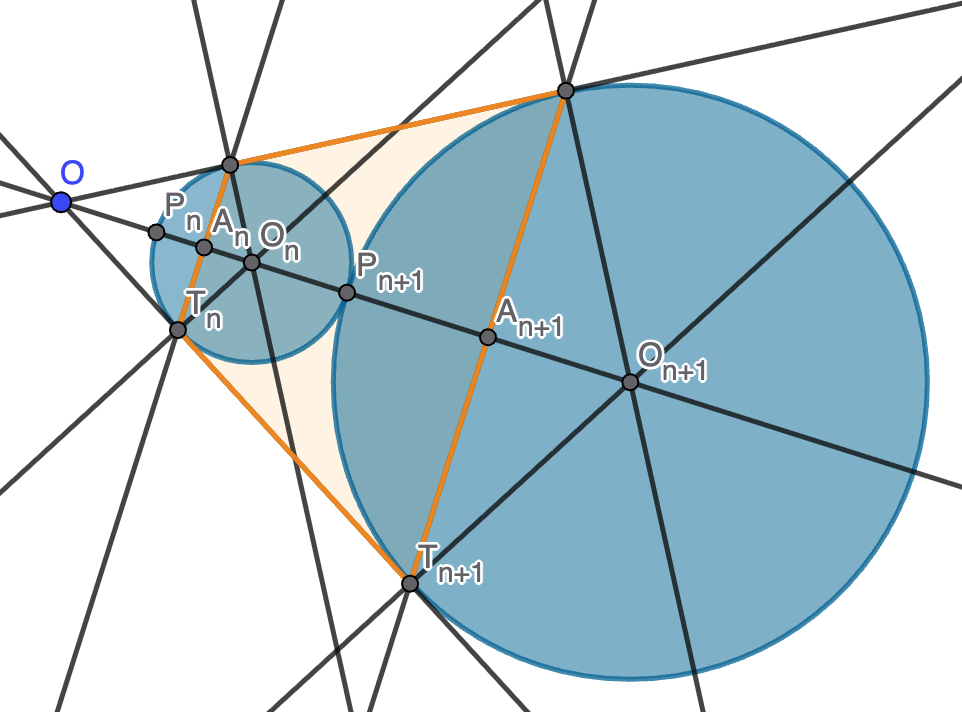
En cuanto al volumen, observamos que éste se puede calcular como el del cono truncado que surge al revolucionar la región naranja al que hay que quitarle dos casquetes esféricos, uno de la esfera $n$-ésima y otro de la esfera $(n+1)$-ésima. Vamos por partes:
- En el triángulo $OT_nO_n$ podemos calcular $\tan(30)=\frac{r_n}{OT_n}$, de donde $OT_n=r_n\sqrt{3}$. Ahora en el triángulo $OA_nT_n$ podemos calcular $A_nT_n=OT_n\operatorname{sen}(30)=\frac{\sqrt{3}}{2}r_n$ y $OA_n=OT_n\cos(30)=\frac{3}{2}r_n$. Por tanto, el cono de revolución del triángulo $OA_nT_n$ tiene volumen $V_n=\frac{1}{3}\pi(A_nT_n)^2(OA_n)=\frac{3}{8}\pi r_n^3$. El volumen de revolución del trapecio naranja será $V_{n+1}-V_n=\frac{3}{8}\pi(r_{n+1}^3-r_n^3)=\frac{39}{4}\pi r_n^3$.
- Como el triángulo $O_{n+1}P_{n+1}T_{n+1}$ es equilátero, $A_{n+1}$ es el punto medio de $P_{n+1}O_{n+1}$. Esto nos dice que buscamos el volumen de un casquete de la esfera $(n+1)$-ésima de altura la mitad su radio. La fórmula para el volumen del casquete nos da $\frac{5}{24}\pi r_{n+1}^3=\frac{45}{8}\pi r_n^3$.
- El mismo casquete en la esfera $n$-ésima tiene volumen $\frac{5\pi}{24}r_n^3$, pero en este caso necesitamos el casquete complementario, cuyo volumen será $\frac{4}{3}\pi r_n^3-\frac{5}{24}\pi r_n^3=\frac{9}{8}\pi r_n^3$.
Con todo esto, el volumen que buscamos para el apartado (b) es \[\frac{39}{4}\pi r_n^3-\frac{45}{8}\pi r_n^3-\frac{9}{8}\pi r_n^3=3\pi r_n^3.\]
Nota. El volumen de un casquete esférico de altura $h$ en una esfera de radio $r$ es $\frac{\pi}{3}h^2(3r-h)$.
Informar de error en enunciado Informar de procedencia del problema
Nota. En un triángulo rectángulo de hipotenusa $a$ y catetos $b$ y $c$, el área se puede calcular como $\frac{1}{2}bc$, ya que los catetos hacen de base y altura, y también como $S=rp=\frac{1}{2}(a+b+c)r$. Igualando ambas expresiones, obtenemos que $r=\frac{bc}{a+b+c}$.
Informar de error en enunciado Informar de procedencia del problema
- Demostrar que $PA^2+PB^2$ no depende de la cuerda trazada.
- Hallar la longitud de la cuerda $AB$ que hace máxima el área del triángulo $ABP$.
En cuanto al apartado (b), el área de $ABP$ se calcula como \[\operatorname{Area}(ABP)=\frac{1}{2}AB\cdot AA'=\frac{1}{2}2r\cos\theta\cdot r\operatorname{sen}\theta=r^2\operatorname{sen}(2\theta).\] Esta área es máxima claramente cuando $\operatorname{sen}(2\theta)=1$, es decir, cuando $\theta=45^\circ$, en cuyo caso obtenemos la longitud $AB=2r\cos\theta=r\sqrt{2}$.
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema