Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2764 problemas y 1057 soluciones.
Problema 1684
ASU, 1972-P1
Sea $ABCD$ un rectángulo y sean $M$ el punto medio de $AD$ y $N$ el punto medio de $BC$. Sea $P$ un punto del plano tal que $D$ está en el segmento $CP$ y supongamos que la semirrecta $PM$ corta a $AC$ en un punto $Q$. Demostrar que la recta $MN$ es la bisectriz del ángulo $\angle PNQ$.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 1682
Dibujado el triángulo de vértices $A,B,C$, se pide determinar gráficamente el punto $P$ tal que
\[\angle PAB=\angle PBC=\angle PCA.\]
Expresar una función trigonométrica de este ángulo $\angle PAB$ en función de las funciones trigonométricas de los ángulos $A$, $B$ y $C$.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 1679
Dadas dos circunferencias exteriores de radios $r$ y $r'$ ($r\neq r'$), se pide dibujar, razonadamente, una recta paralela a una dirección dada, tal que determine sobre las dos circunferencias dos cuerdas tales que la suma de sus longitudes sea igual a una longitud dada $\ell$.
pistasolución 1info
Pista. Quédate con dos semicírculos de forma que el problema se reduzca a que la suma de longitudes sea $\frac{\ell}{2}$.
Solución. Por simplicidad, supongamos que la dirección dada es la horizontal y que el centro $O$ de la circunferencia $\Gamma$ de radio $r$ está a la izquierda (o sobre la misma vertical) que el centro de la circunferencia $\Gamma'$ de radio $r'$. Cortamos $\Gamma$ y $\Gamma'$ por sus diámetros verticales y consideramos $C$ la semicircunferencia izquierda de $\Gamma$ y $C'$ la semicircunferencia derecha de $\Gamma'$. Trasladamos horizontalmente $C'$ hasta otra semicircunferencia $C''$ para que su diámetro se superponga con el de $C$, creando así la figura sombreada en la imagen. Como esta figura está compuesta por dos semicírculos, será suficiente encontrar un segmento en la dirección dada de longitud $\frac{\ell}{2}$. Para ello sólo hay que desplazar la figura una distancia $\frac{\ell}{2}$ a la derecha y tomar los puntos $X$ donde el borde de figura trasladada (en rojo en la imagen) se corte con el borde original (en verde). Por estos puntos $X$ pasarán las rectas que buscamos.
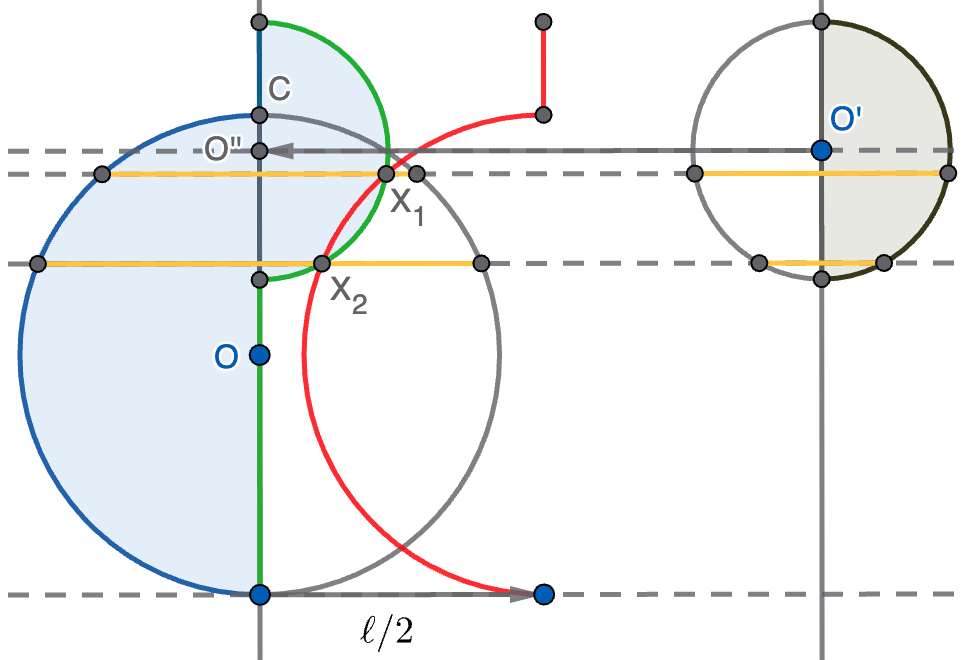
En la imagen se tiene un ejemplo, donde hay exactamente dos soluciones $X_1$ y $X_2$, para cada una de las cuales se ha indicado los segmentos cuyas longitudes suman $\ell$ en amarillo.

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 1675
Sean $A'$, $B'$ y $C'$ los puntos de tangencia de los lados $BC$, $CA$ y $AB$, respectivamente, de un triángulo con su circunferencia inscrita. Sea $D$ el punto de intersección de $C'A'$ con la bisectriz del ángulo del vértice $A$. Calcular el valor del ángulo $\angle ADC$.
pistasolución 1info
Pista. Demuestra que la circunferencia circunscrita a $A'DC$ pasa por el incentro del triángulo $ABC$.
Solución. Por comodidad, llamaremos $\alpha,\beta,\gamma$ a los ángulos del triángulo, como es usual. El triángulo $BAC'$ es isósceles, luego $\angle DC'A=180^\circ-\angle BC'A'=180^\circ-\frac{1}{2}(180^\circ-\beta)=90^\circ+\beta$. Por lo tanto, en el triángulo $AC'D$, tenemos que $\angle C'DA=180^\circ-\angle DC'A-\frac{\alpha}{2}=90-\frac{\alpha+\beta}{2}=\frac{\gamma}{2}$. Ahora bien, como $AD$ es la bisectriz y contiene al incentro $I$, deducimos que $\angle A'DI=\angle\frac{\gamma}{2}=\angle ICA'$. Por la propiedad del arco capaz, esto nos dice que $ICDA'$ es un cuadrilátero cíclico y, por tanto,
\[\angle ADC=\angle IDC=\angle IA'C=90^\circ.\]
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 1671
Tres puntos $A',B',C'$ están situados, respectivamente, sobre los lados $BC,CA,AB$ de un triángulo dado $ABC$ de área $S$, de forma que
\[\frac{AC'}{AB}=\frac{BA'}{BC}=\frac{CB'}{CA}=p,\]
siendo $0\lt p\lt 1$ un parámetro variable. Determinar:
- El área del triángulo $A'B'C'$ en función de $p$ y $S$.
- El valor de $p$ que minimiza el área anterior.
- El lugar geométrico al variar $p$ de los puntos $P$ de intersección de las paralelas trazadas por $A'$ y $C'$, respectivamente, a los lados $AB$ y $AC$.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre