Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2764 problemas y 1057 soluciones.
Problema 1679
Dadas dos circunferencias exteriores de radios $r$ y $r'$ ($r\neq r'$), se pide dibujar, razonadamente, una recta paralela a una dirección dada, tal que determine sobre las dos circunferencias dos cuerdas tales que la suma de sus longitudes sea igual a una longitud dada $\ell$.
pistasolución 1info
Pista. Quédate con dos semicírculos de forma que el problema se reduzca a que la suma de longitudes sea $\frac{\ell}{2}$.
Solución. Por simplicidad, supongamos que la dirección dada es la horizontal y que el centro $O$ de la circunferencia $\Gamma$ de radio $r$ está a la izquierda (o sobre la misma vertical) que el centro de la circunferencia $\Gamma'$ de radio $r'$. Cortamos $\Gamma$ y $\Gamma'$ por sus diámetros verticales y consideramos $C$ la semicircunferencia izquierda de $\Gamma$ y $C'$ la semicircunferencia derecha de $\Gamma'$. Trasladamos horizontalmente $C'$ hasta otra semicircunferencia $C''$ para que su diámetro se superponga con el de $C$, creando así la figura sombreada en la imagen. Como esta figura está compuesta por dos semicírculos, será suficiente encontrar un segmento en la dirección dada de longitud $\frac{\ell}{2}$. Para ello sólo hay que desplazar la figura una distancia $\frac{\ell}{2}$ a la derecha y tomar los puntos $X$ donde el borde de figura trasladada (en rojo en la imagen) se corte con el borde original (en verde). Por estos puntos $X$ pasarán las rectas que buscamos.
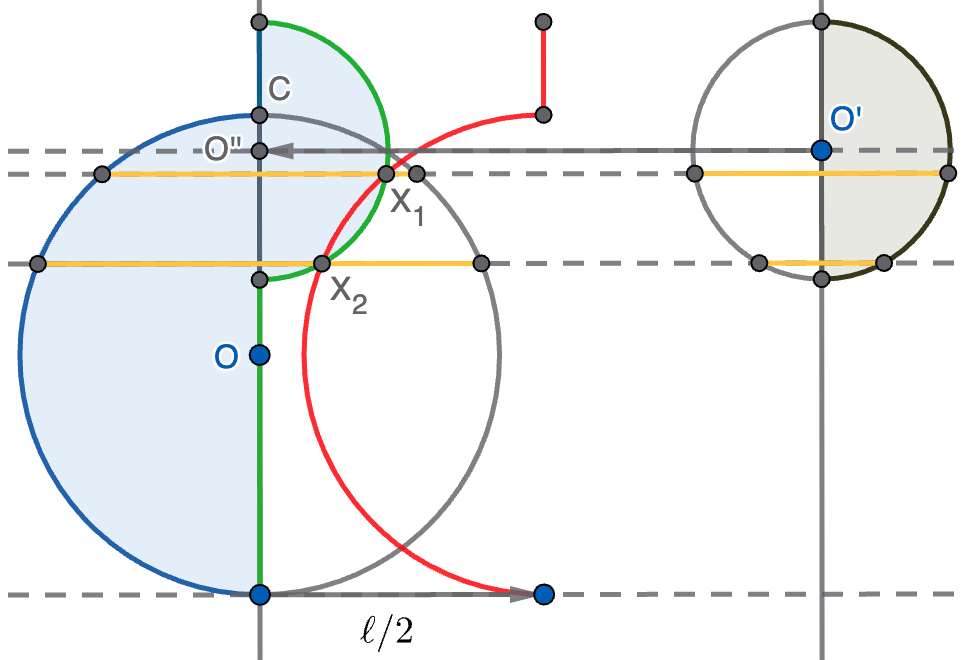
En la imagen se tiene un ejemplo, donde hay exactamente dos soluciones $X_1$ y $X_2$, para cada una de las cuales se ha indicado los segmentos cuyas longitudes suman $\ell$ en amarillo.

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 1675
Sean $A'$, $B'$ y $C'$ los puntos de tangencia de los lados $BC$, $CA$ y $AB$, respectivamente, de un triángulo con su circunferencia inscrita. Sea $D$ el punto de intersección de $C'A'$ con la bisectriz del ángulo del vértice $A$. Calcular el valor del ángulo $\angle ADC$.
pistasolución 1info
Pista. Demuestra que la circunferencia circunscrita a $A'DC$ pasa por el incentro del triángulo $ABC$.
Solución. Por comodidad, llamaremos $\alpha,\beta,\gamma$ a los ángulos del triángulo, como es usual. El triángulo $BAC'$ es isósceles, luego $\angle DC'A=180^\circ-\angle BC'A'=180^\circ-\frac{1}{2}(180^\circ-\beta)=90^\circ+\beta$. Por lo tanto, en el triángulo $AC'D$, tenemos que $\angle C'DA=180^\circ-\angle DC'A-\frac{\alpha}{2}=90-\frac{\alpha+\beta}{2}=\frac{\gamma}{2}$. Ahora bien, como $AD$ es la bisectriz y contiene al incentro $I$, deducimos que $\angle A'DI=\angle\frac{\gamma}{2}=\angle ICA'$. Por la propiedad del arco capaz, esto nos dice que $ICDA'$ es un cuadrilátero cíclico y, por tanto,
\[\angle ADC=\angle IDC=\angle IA'C=90^\circ.\]
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 1671
Tres puntos $A',B',C'$ están situados, respectivamente, sobre los lados $BC,CA,AB$ de un triángulo dado $ABC$ de área $S$, de forma que
\[\frac{AC'}{AB}=\frac{BA'}{BC}=\frac{CB'}{CA}=p,\]
siendo $0\lt p\lt 1$ un parámetro variable. Determinar:
- El área del triángulo $A'B'C'$ en función de $p$ y $S$.
- El valor de $p$ que minimiza el área anterior.
- El lugar geométrico al variar $p$ de los puntos $P$ de intersección de las paralelas trazadas por $A'$ y $C'$, respectivamente, a los lados $AB$ y $AC$.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 1666
Los puntos $A',B',C'$ se encuentran respectivamente sobre los lados $BC,CA,AB$ del triángulo $ABC$ y cumplen que
\[\frac{AC'}{C'B}=\frac{BA'}{A'C}=\frac{CB'}{B'A}=k.\]
Las rectas $AA',BB',CC'$ forman un triángulo $A_1B_1C_1$. En función de $k$ y del área $S$ del triángulo $ABC$, calcular el área del triángulo $A_1B_1C_1$.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 1663
Es muy conocido el puzzle consistente en descomponer la cruz griega de la
izquierda de la figura en cuatro partes con las que se pueda componer un cuadrado. Una solución habitual es la de la figura de la derecha. Demostrar que hay una infinidad de soluciones diferentes. ¿Hay alguna solución que dé lugar a cuatro partes iguales?

Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre