Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2764 problemas y 1057 soluciones.
Problema 1580
En el plano tenemos una recta $r$ y dos puntos $A$ y $B$ que no pertenecen a $r$ pero se encuentran en el mismo semiplano determinado por ella. Determinar un punto $M$ de la recta tal que el ángulo de $r$ con $AM$ sea doble del de $r$ con $BM$ (considerando como ángulo de dos rectas el menor de los ángulos que forman).
pistasolución 1info
Pista. Intenta que $BM$ sea la bisectriz del ángulo que forman $r$ y $AM$ y procura no dejar ningún caso sin analizar.
Solución. Trazamos la circunferencia $\Gamma$ de centro $B$ que es tangente a $r$, la semicircunferencia de $\Gamma$ más distante de $r$ (marcada en azul en la figura superior) y la región entre dicha circunferencia y $r$ (marcada en rosa en la figura superior). También consideramos las semirrectas paralelas a $r$ que se proyectan fuera de $\Gamma$ (marcadas en verde en la figura superior). Distinguimos dos casos:
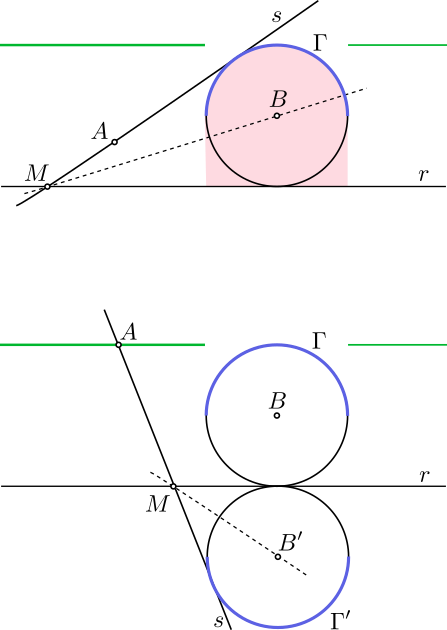
- Supongamos que $A$ no está en la región marcada en rosa. Entonces trazamos una recta tangente $s$ a $\Gamma$ que pase por $A$ y corte a $\Gamma$ en la semicircunferencia azul.
- Si $A$ no está en ninguna de las dos semirrectas paralelas a $r$ marcadas en verde, entonces podemos tomar $s$ que no sea paralela a $r$ y definimos $M$ como el punto de corte de $s$ y $r$. Entonces, $BM$ es la bisectriz del ángulo (menor de $90^\circ$) que forman $r$ y $AM$, luego se cumple la propiedad que queremos.
- Si $A$ está en una de las semirrectas marcadas en verde, entonces tomamos la circunferencia $\Gamma'$ simétrica de $\Gamma$ respecto de $r$ y $s$ una tangente a $\Gamma'$ en un punto de la semicircunferencia simétrica del original. Definimos de nuevo $M$ como el punto de corte de $s$ y $r$. Como $MB'$ es la bisectriz del ángulo menor de $90^\circ$ que forman $r$ y $s'$, se tiene que el ángulo que forman $MB$ y $r$ es igual al que forman $MB'$ y $r'$ y por tanto también se cumple la propiedad.
- Supongamos ahora que $A$ está en la región marcada de rojo. Entonces, las tangentes a $\Gamma$ o $\Gamma'$ son las únicas candidatas a cumplir la propiedad que deseamos y todas ellas la cumplen pero solo si consideramos el ángulo mayor que forman con $r$, no el menor como se especifica en el enunciado. Concluimos que en este caso el problema no tiene solución.

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 1575
Un depósito tiene forma de prisma hexagonal regular cuyas bases son de $1$ m de lado y su altura es de $10$ m. Se sitúan las aristas laterales en posición oblicua y se llena parcialmente con $9$ m$^3$ de agua. Sabiendo que el plano de la superficie libre del agua corta a todas las aristas laterales y que una de ellas queda con una parte de $2$ m bajo el agua. ¿Qué parte queda bajo el agua en la arista lateral opuesta del prisma?
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 1574
En una circunferencia de radio igual a la unidad se trazan dos cuerdas $AB$ y $AC$ de igual longitud.
- Averiguar cómo se puede construir una tercera cuerda $DE$ que quede dividida en tres partes iguales por las intersecciones con $AB$ y $AC$.
- Si $AB=AC=\sqrt{2}$, ¿cuánto valen las longitudes de los dos segmentos que la cuerda $DE$ determina sobre $AB$?
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 1572
Los tres lados de un triángulo equilátero se suponen reflectantes (excepto en los vértices), de forma que reflejen hacia dentro del triángulo los rayos de luz situados en su plano, que incidan sobre ellos y que salgan de un punto interior del triángulo. Determinar el recorrido de un rayo de luz que, partiendo de un vértice del triángulo alcance a otro vértice del mismo después de reflejarse sucesivamente en los tres lados. Calcular la longitud del camino seguido por la luz suponiendo que el lado del triángulo mide $1$ m.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 1567
En el plano se consideran los puntos $P=(8,2)$ y $Q=(5,11)$. Determinar el camino de longitud mínima para ir de $P$ a $Q$ con las siguientes condiciones: partiendo de $P$, llegamos a un punto del eje $x$ y recorremos un segmento de longitud $1$ a lo largo de este eje; después, nos separamos hasta llegar a un punto del eje $y$ y recorremos un segmento de longitud $2$ en este eje, para finalmente dirigirnos al punto $Q$. Hallar la longitud de dicho camino.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre