Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2764 problemas y 1057 soluciones.
Problema 1572
Los tres lados de un triángulo equilátero se suponen reflectantes (excepto en los vértices), de forma que reflejen hacia dentro del triángulo los rayos de luz situados en su plano, que incidan sobre ellos y que salgan de un punto interior del triángulo. Determinar el recorrido de un rayo de luz que, partiendo de un vértice del triángulo alcance a otro vértice del mismo después de reflejarse sucesivamente en los tres lados. Calcular la longitud del camino seguido por la luz suponiendo que el lado del triángulo mide $1$ m.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 1567
En el plano se consideran los puntos $P=(8,2)$ y $Q=(5,11)$. Determinar el camino de longitud mínima para ir de $P$ a $Q$ con las siguientes condiciones: partiendo de $P$, llegamos a un punto del eje $x$ y recorremos un segmento de longitud $1$ a lo largo de este eje; después, nos separamos hasta llegar a un punto del eje $y$ y recorremos un segmento de longitud $2$ en este eje, para finalmente dirigirnos al punto $Q$. Hallar la longitud de dicho camino.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 1566problema obsoleto
Se considera un triángulo equilátero de altura $1$. Para todo punto $P$ del interior del triángulo, se designan por $x, y, z$ las distancias de $P$ a los lados del triángulo.
- Probar que $x+y+z=1$.
- Determinar los puntos $P$ para los que la distancia a un lado es mayor que la suma de las distancias a los otros dos.
- Tenemos una barra de longitud 1 y la rompemos en tres trozos. Hallar la probabilidad de que con estos trozos se pueda formar un triángulo.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 1564
Sean $C$ y $C'$ dos circunferencias concéntricas de radios $r$ y $r'$, respectivamente. Determinar cuánto ha de valer el cociente $r'/r$ para que en la corona limitada por $C$ y $C'$ existan ocho circunferencias $C_1,C_2,\ldots,C_8$ que sean tangentes a $C$ y $C'$ y también que cada $C_i$ sea tangente exterior a $C_{i+1}$ para $1\leq i\leq 7$ y $C_8$ sea tangente exterior a $C_1$.
pistasolución 1info
Pista. Resuelve el triángulo cuyos vértices son el centro común de $C$ y $C'$, el centro de $C_1$ y el punto de tangencia de $C_1$ y $C_2$.
Solución. Supondremos que $C'$ es la circunferencia exterior. Por simetría, cada una de las circunferencias $C_1,C_2,\ldots,C_8$ tiene que estar inscrita en un sector angular de $45^\circ$. Todas ellas tienen que tener el mismo radio, que llamaremos $\rho$ y debe cumplirse que $r'=r+2\rho$ ya que un radio de $C'$ se puede expresar como suma de un radio de $C$ y del diámetro de cualquier $C_i$. Además, considerando el triángulo indicado en la figura, podemos calcular el seno de $22,5^\circ$ como el cateto opuesto $\rho$ dividido por la hipotenusa $r+\rho$. El seno de este ángulo se puede calcular por la fórmula del ángulo mitad (ver la nota), lo que nos da
\[\tfrac{1}{2}\sqrt{2-\sqrt{2}}=\operatorname{sen}(22.5)=\frac{\rho}{r+\rho}=\frac{r'-r}{r'+r}=\frac{\frac{r'}{r}-1}{\frac{r'}{r}+1},\]
luego podemos despejar
\[\frac{r'}{r}=\frac{1+\tfrac{1}{2}\sqrt{2-\sqrt{2}}}{1-\tfrac{1}{2}\sqrt{2-\sqrt{2}}}=7-4 \sqrt{2}+2 \sqrt{20-14 \sqrt{2}}.\]
¿Sabrías justificar esta última racionalización?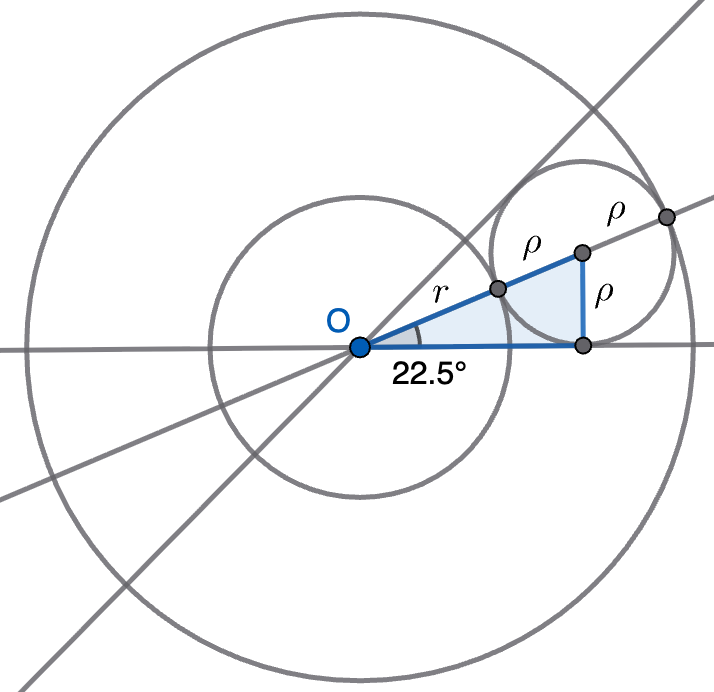

Nota. La fórmula del seno del ángulo mitad nos dice que \[\operatorname{sen}^2(\tfrac{x}{2})=\frac{1-\cos(x)}{2}.\] En el caso $x=45$, hay que darse cuenta también de que $\operatorname{sen}(\tfrac{x}{2})$ es positivo.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 1559
Dadas tres circunferencias de radios $r$, $r'$ y $r''$, cada una tangente exteriormente a las otras dos, calcular el radio del círculo inscrito al triángulo cuyos vértices son los centros de las tres circunferencias.
pistasolución 1info
Pista. Utiliza que el área de un triángulo es igual a su semiperímetro multiplicado por el radio de su circunferencia inscrita.
Solución. Los lados del triángulo son $a=r+r'$, $b=r'+r''$ y $c=r''+r$, luego el radio de su circunferencia inscrita $\rho$ puede calcularse mediante la fórmula $S=\rho p$, siendo $S$ el área del triángulo y $p=\frac{1}{2}(a+b+c)=r+r'+r''$ su semiperímetro. Usando la fórmula de Herón, tenemos que
\[\rho=\frac{S}{p}=\frac{\sqrt{p(p-a)(p-b)(p-c)}}{p}=\sqrt{\frac{r\cdot r'\cdot r''}{r+r'+r''}}.\]
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre