Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| OMCC |
| Retos UJA |
Buscar problemas
Informar de error en enunciado Informar de procedencia del problema
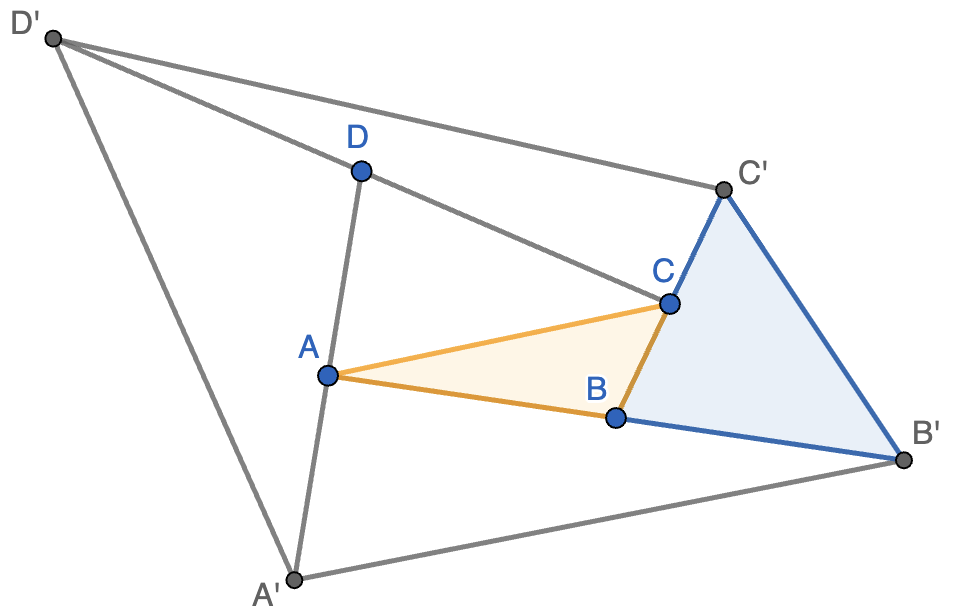
- Los puntos $A$ y $B$ se mueven con la misma velocidad angular constante y en el sentido de las agujas del reloj a lo largo de sendas circunferencias de centros $O_a$ y $O_b$. Demostrar que el vértice $C$ de un triángulo equilátero $ABC$ también se mueve uniformemente recorriendo cierta circunferencia.
- Si $ABC$ es un triángulo equilátero y un punto $P$ cumple $AP=2$ y $BP=3$, hallar el valor máximo posible de $CP$.
El apartado (b) es consecuencia de la desigualdad de Ptolomeo aplicada a los cuatro puntos $A,C,B,P$, que nos dice que \[CP\cdot AB\leq AP\cdot BC+BP\cdot AC\ \Longleftrightarrow\ CP\leq AP+BP=2+3=5,\] ya que $AB=BC=CA$. Además, sabemos que si $ACBP$ es un cuadrilátero cíclico, entonces la igualdad se alcanza. Por tanto, el máximo anterior $CP=5$ se alcanza cuando $P$ está en el arco menor $AB$ de la circunferencia circunscrita del triángulo $ABC$. En este caso, el triángulo $ABP$ tiene lados $AP=2$ y $BP=3$ que forman un ángulo de $120^\circ$ por la propiedad del arco capaz, de forma que el teorema del coseno nos da necesariamente \[AB^2=2^2+3^2-2\cdot 2\cdot 3\cos(120^\circ)=19.\] Deducimos así que el máximo $CP=5$ se alcanza efectivamente para un triángulo de lado $\sqrt{19}$ cuando el punto $P$ está en el arco menor $AB$.
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
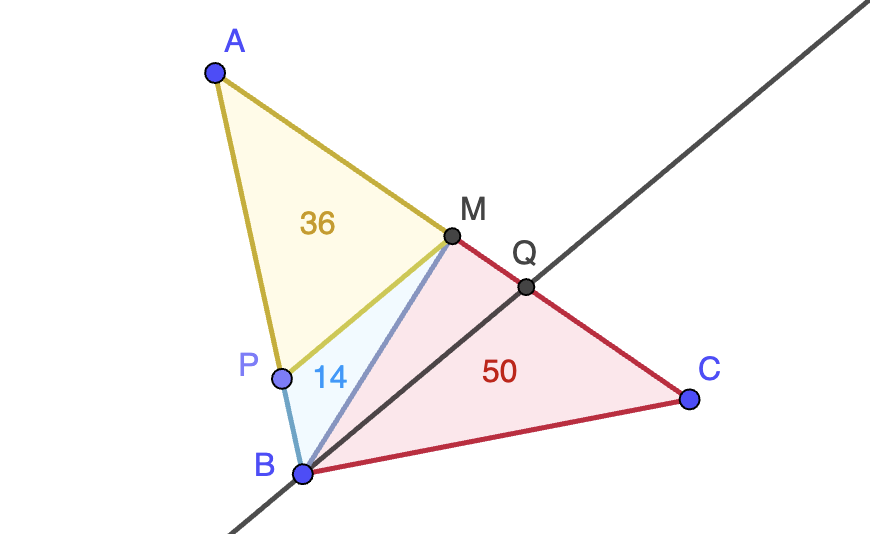
Nota. No es difícil terminar el razonamiento y ver que las soluciones al problema son \[(a,b)=\left(21\sqrt{3},5\sqrt{3}\right)\qquad\text{y}\qquad (a,b)=\left(-21\sqrt{3},-5\sqrt{3}\right).\]
Informar de error en enunciado Informar de procedencia del problema
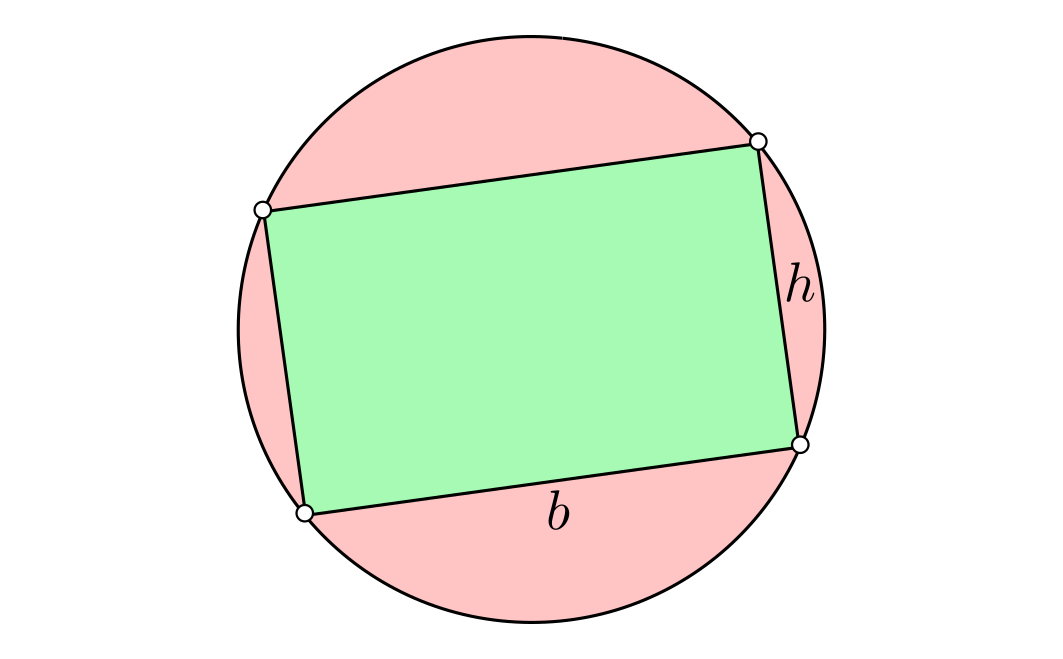
Nota. Otra opción para finalizar el ejercicio es darse cuenta de que el siguiente cociente es mayor que $1$: \[\frac{A}{A'}=\frac{\frac{b}{h}}{\frac{\pi}{4}((\frac{b}{h})^2+1)-\frac{b}{h}}=\frac{\frac{1+\sqrt{5}}{2}}{\frac{\pi}{4}((\frac{1+\sqrt{5}}{2})^2+1)-\frac{1+\sqrt{5}}{2}}\approx 1.32,\] donde hemos dividido numerador y denominador por $h^2$ para poder aplicar ($\star$). Una alternativa a esto último es suponer a lo largo de todo el razonamiento que $h=1$ haciendo previamente una homotecia.
Informar de error en enunciado Informar de procedencia del problema