Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2764 problemas y 1057 soluciones.
Problema 1428
Se construye con alambre un triángulo equilátero de lado $\ell$ y se deposita sobre una esfera maciza de radio $r$ (que no pasa a través del triángulo). ¿A qué distancia del centro de la esfera quedan los vértices del triángulo?
pistasolución 1info
Pista. Observa que la esfera es tangente a los tres lados del triángulo. Busca triángulos rectángulos que se formen entre el centro de la esfera, los vértices del triángulo y los puntos de tangencia.
Solución. Sea $ABC$ el triángulo equilátero, $M$ el punto medio del lado $AB$ y $O$ el centro de la esfera. El lado $AB$ es tangente a la esfera en $M$, luego perpendicular a $OM$, de forma que $AOM$ es un triángulo rectángulo y el teorema de Pitágoras nos asegura que
\[AO^2=OM^2+MA^2=R^2+\frac{\ell^2}{4},\]
luego la distancia que nos piden es $AO=\sqrt{R^2+\frac{\ell^2}{4}}$.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 1423
Un triángulo equilátero inscrito en una circunferencia de centro $O$ y radio igual a $4$cm, se gira un ángulo recto en torno a $O$. Hallar el área de la parte común al triángulo dado y al obtenido en ese giro.
pistasolución 1info
Pista. Los dos triángulos tienen en común un hexágono y el resto son seis triángulos rectángulos iguales entre sí.
Solución. Sea $ABC$ el triángulo y $A'B'C'$ el triángulo rotado $90^\circ$, como se indica en la figura (estamos interesados en hallar el área de color naranja). Los seis triángulos pintados de azul son congruentes entre sí ya que las líneas discontinuas son ejes de simetría (¿por qué?). Consideramos los puntos de intersección $D$ y $E$ de $B'C'$ con $AC$ y $BD$, respectivamente. Tenemos entonces que $\angle DCE=\angle BCA=60^\circ$ y $\angle DEC=90^\circ$ porque $B'C'$ es una rotación de $90^\circ$ de $BC$. Por lo tanto, el triángulo $CDE$ es rectángulo y cumple que
\[CE=CD\,\mathrm{sen}(30^\circ)=\tfrac{1}{2}CD,\qquad\qquad CE=CD\,\mathrm{cos}(30^\circ)=\tfrac{\sqrt{3}}{2}CD.\]
Ahora usamos que $CD+DE+EC=C'D+DE+EB'=B'C'=4\sqrt{3}$ (ver la nota). Esto nos dice que
\[\tfrac{1}{2}CD+CD+\tfrac{\sqrt{3}}{2}CD=4\sqrt{3}\ \Longleftrightarrow\ CD=\frac{8\sqrt{3}}{3+\sqrt{3}}.\]
Por tanto, el área de cada triángulo azul será
\[\text{Área}(CDE)=\frac{1}{2}DE\cdot EC=\frac{\sqrt{3}}{8}\left(\frac{8\sqrt{3}}{3+\sqrt{3}}\right)^2=8\sqrt{3}-12.\]
Finalmente, el área que buscamos se calcula como el área de $ABC$, que es igual a $12\sqrt{3}$ (ver la nota), menos tres veces el área de $CDE$, luego el resultado es, en centímetros cuadrados:
\[12\sqrt{3}-3\cdot (8\sqrt{3}-12)=36-12\sqrt{3}.\]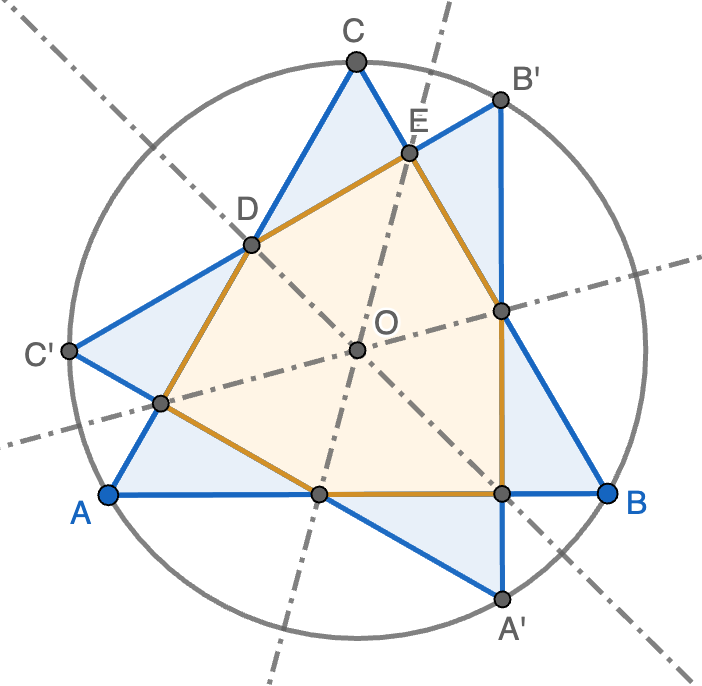

Nota. Hemos usado que si $\ell$ es el lado de un triángulo regular, entonces el radio de su circunferencia circunscrita es $R=\frac{\ell}{\sqrt{3}}$ y su área es $S=\frac{\sqrt{3}}{4}\ell^2$. ¿Sabrías probarlo?
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 1419
Dado un pentágono regular, se dibujan sus cinco segmentos diagonales. Se pide determinar el número total de triángulos que aparecen construidos en la figura y clasificar este conjunto de triángulos en clases de triángulos congruentes entre sí.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 1413
IMO, 1967-P4
Sean $A_0B_0C_0$ y $A_1B_1C_1$ dos triángulos acutángulos. Consideremos todos los triángulos $ABC$ que son semejantes a $A_1B_1C_1$ y tales que $A_0$ está en el lado $AB$, $B_0$ en $CA$ y $C_0$ en $AB$. De todos los posibles triángulos en estas condiciones, hallar el que tiene mayor área y construirlo.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 1411
IMO, 1967-P2
Demostrar que si una y solo una de las aristas de un tetraedro es mayor que $1$, entonces su volumen es menor o igual que $1/8$.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre