Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2764 problemas y 1057 soluciones.
Problema 1203
IMO, 1959-P5
Se elige un punto arbitrario $M$ en el interior de un segmento $AB$. Se toman cuadrados $AMCD$ y $MBEF$ al mismo lado de $AB$, siendo los segmentos $AM$ y $MB$ sus bases. Las circunferencias circunscritas a estos cuadrados, con centros en $P$ y $Q$, se cortan en $M$ y también en otro punto $N$. Sea $N'$ el punto de intersección de las rectas $AF$ y $BC$.
- Demostrar que los puntos $N$ y $N'$ coinciden.
- Demostrar que la recta $MN$ pasa por un punto $S$ al variar $M$.
- Encontrar el lugar geométrico del punto medio del segmento $PQ$ al variar $M$.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 1202
IMO, 1959-P4
Construir con regla y compás un triángulo rectángulo conociendo la hipotenusa $c$ y que la mediana que une el vértice del ángulo recto con el punto medio de la hipotenusa es la media geométrica de los dos catetos del triángulo.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 1191
ASU, 1965-P7
En un triángulo se traza una recta tangente a la circunferencia inscrita que es paralela a uno de los lados y corta a los otros dos en los puntos $X$ e $Y$. ¿Cuál es la mayor distancia posible $XY$ en términos del perímetro del triángulo?
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 1187
ASU, 1965-P3
Sea $\Gamma$ la circunferencia circunscrita al triángulo $ABC$. Sean $X$, $Y$ y $Z$ los puntos medios de los arcos $BC$, $AC$ y $AB$ de $\Gamma$ que no contienen a $A$, $B$ y $C$, respectivamente. Supongamos que $YZ$ corta a $AB$ en $D$ y que $XY$ corta a $BC$ en $E$. Demostrar que $DE$ es paralela a $AC$ y que pasa por el incentro de $ABC$.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 1181
ASU, 1964-P10
Un círculo de centro $O$ está inscrito en un cuadrilátero $ABCD$. Demostrar que
\[\angle AOB+\angle COD=180^\circ.\]
pistasolución 1info
Pista. Si $M$ y $N$ son los puntos medios de $AB$ y $BC$, entonces fíjate en que $BOM$ y $NOB$ son congruentes.
Solución. Sean $M,N,P,Q$ los puntos medios de los lados $AB,BC,CD,DA$, respectivamente, tal y como se indica en la figura. Los triángulos $AMO$ y $BNO$ son congruentes ya que $MB=BN$ y $\angle MBO=\angle NBO$ por la tangencia y también $BO$ es común a ambos triángulos. Por esto, se tiene que $\angle MOB=\angle NOB$. De la misma manera, se prueba que $\angle NOC=\angle POC$, que $\angle POD=\angle DOQ$ y que $\angle QOA=\angle AOM$. En la figura, se indican con el mismo color ángulos iguales, luego está claro que $\angle AOB+\angle COD=180^\circ$ ya que esta suma tiene un ángulo de cada color y el doble sería el ángulo completo de $360^\circ$.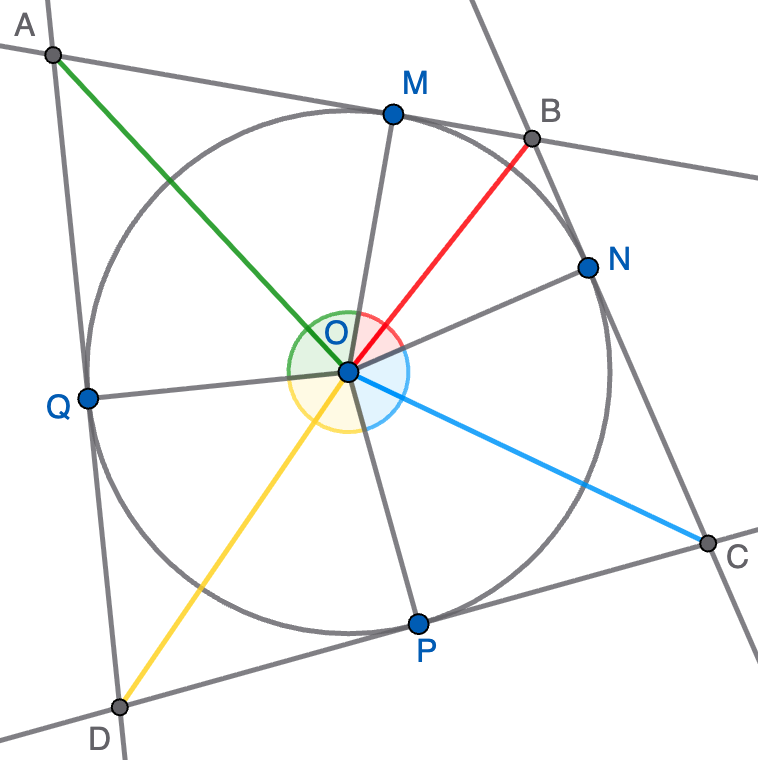

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre