Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
- Demostrar que $KP$ pasa por un punto fijo cuando varía $M$.
- Hallar el lugar geométrico de $P$ cuando varía $M$.
Informar de error en enunciado Informar de procedencia del problema
- Si cada una de las diagonales de un cuadrilátero convexo lo divide en dos triángulos de igual área, demostrar que se trata de un paralelogramo.
- Si cada una de las tres diagonales principales (que unen vértices opuestos) de un hexágono convexo lo divide en dos cuadriláteros de igual área, demostrar que estas tres diagonales tienen un punto en común.
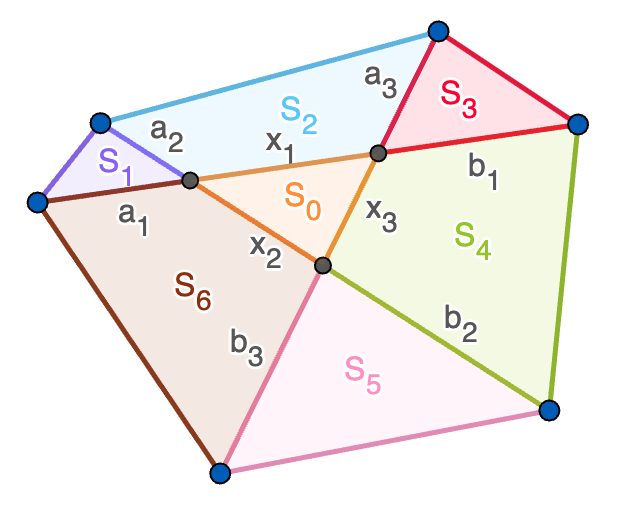
En cuanto al apartado (b), supongamos que tenemos un hexágono convexo que cumple la propiedad del enunciado pero no sabemos si las diagonales se cortan en el mismo punto. Estas diagonales dividen al hexágono en siete regiones de áreas $S_0,\ldots,S_6$ y denotamos por $a_1,a_2,a_3$, $b_1,b_2,b_3$ y $x_1,x_2,x_3$ los segmentos que se forman, todo ello como se indica en la figura. Las igualdades de las áreas se traducen en \begin{align*} S_1+S_2+S_3&=S_0+S_4+S_5+S_6,\\ S_3+S_4+S_5&=S_0+S_6+S_1+S_2,\\ S_5+S_6+S_1&=S_0+S_2+S_3+S_4. \end{align*} Sumando estas igualdades dos a dos, obtenemos que \[S_1=S_0+S_4,\qquad S_2=S_0+S_5,\qquad S_3=S_0+S_6,\] Tenemos que $S_1$ es el área de un triángulo que se puede calcular como la mitad del producto de $a_1$ y $a_2$ por el seno del ángulo que forman estos dos lados y que $S_0+S_4$ es el área de otro triángulo que análogamente es la mitad del producto de $x_1+b_1$ y $x_2+b_2$ por el seno del ángulo que forman estos dos segmentos. Los dos ángulos que se han considerado son opuestos por el vértice luego sus senos pueden simplificarse en la igualdad $S_1=S_0+S_4$, obteniendo que \[S_1=S_0+S_4\ \Longleftrightarrow\ a_1a_2=(b_1+x_1)(b_2+x_2)\] y de la misma forma \begin{align*} S_2=S_0+S_5&\ \Longleftrightarrow\ a_3b_1=(b_3+x_3)(a_1+x_1), S_3=S_0+S_6&\ \Longleftrightarrow\ b_2b_3=(a_2+x_2)(a_3+x_3). \end{align*} Multiplicando las tres igualdades así obtenidas, llegamos a que \[a_1a_2a_3b_1b_2b_3=(a_1+x_1)(a_2+x_2)(a_3+x_3)(b_1+x_1)(b_2+x_2)(b_3+x_3),\] pero como todos los números son positivos, el miembro de la derecha es estrictamente mayor que el de la izquierda a menos que $x_1=x_2=x_3=0$, lo que equivale a que las tres diagonales se corten en un único punto.
Informar de error en enunciado Informar de procedencia del problema