Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
- Los puntos $A$ y $B$ se mueven con la misma velocidad angular constante y en el sentido de las agujas del reloj a lo largo de sendas circunferencias de centros $O_a$ y $O_b$. Demostrar que el vértice $C$ de un triángulo equilátero $ABC$ también se mueve uniformemente recorriendo cierta circunferencia.
- Si $ABC$ es un triángulo equilátero y un punto $P$ cumple $AP=2$ y $BP=3$, hallar el valor máximo posible de $CP$.
El apartado (b) es consecuencia de la desigualdad de Ptolomeo aplicada a los cuatro puntos $A,C,B,P$, que nos dice que \[CP\cdot AB\leq AP\cdot BC+BP\cdot AC\ \Longleftrightarrow\ CP\leq AP+BP=2+3=5,\] ya que $AB=BC=CA$. Además, sabemos que si $ACBP$ es un cuadrilátero cíclico, entonces la igualdad se alcanza. Por tanto, el máximo anterior $CP=5$ se alcanza cuando $P$ está en el arco menor $AB$ de la circunferencia circunscrita del triángulo $ABC$. En este caso, el triángulo $ABP$ tiene lados $AP=2$ y $BP=3$ que forman un ángulo de $120^\circ$ por la propiedad del arco capaz, de forma que el teorema del coseno nos da necesariamente \[AB^2=2^2+3^2-2\cdot 2\cdot 3\cos(120^\circ)=19.\] Deducimos así que el máximo $CP=5$ se alcanza efectivamente para un triángulo de lado $\sqrt{19}$ cuando el punto $P$ está en el arco menor $AB$.
Informar de error en enunciado Informar de procedencia del problema
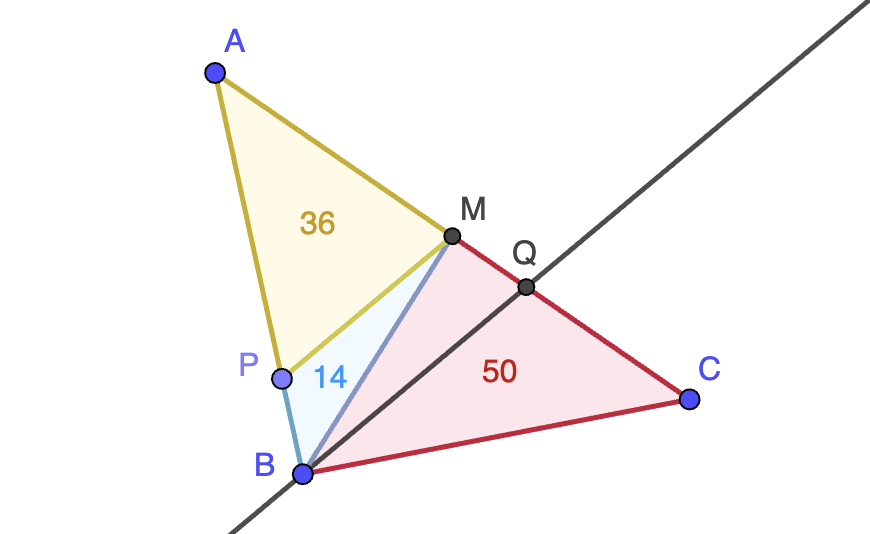
Informar de error en enunciado Informar de procedencia del problema