Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
Informar de error en enunciado Informar de procedencia del problema
Nota. No se puede expresar el resultado final en términos de funciones trigonométricas.
En el pentágono regular de lado $1$ de la figura, los triángulos $ACD$ y $DEP$ son semejantes pues sus lados son paralelos. Si llamamos $d$ a la longitud de la diagonal del pentágono, la semejanza $\frac{AD}{CD}=\frac{DE}{PE}$ se escribe como $\frac{d}{1}=\frac{1}{d-1}$, de donde $d$ cumple la ecuación $d^2-d-1=0$, de la que nos quedamos con la única solución positiva $d=\frac{1+\sqrt{5}}{2}$, la razón áurea. Ahora bien, el triángulo $ABQ$ de la figura es rectángulo y cumple $\angle BAQ=54$, luego \begin{align*}
\mathrm{sen}(54)&=BD=\frac{d}{2}=\frac{1+\sqrt{5}}{4},\\
\cos(54)&=AQ=\sqrt{1-BQ^2}=\sqrt{1-\left(\tfrac{1+\sqrt{5}}{4}\right)^2}=\frac{\sqrt{5-\sqrt{5}}}{2\sqrt{2}}.
\end{align*}
De esta forma, tenemos que el área del triángulo es
\[8\,\mathrm{sen}(54)\cos(54)=8\frac{1+\sqrt{5}}{4}\cdot\frac{\sqrt{5-\sqrt{5}}}{2\sqrt{2}}=\sqrt{10+2\sqrt{5}}.\]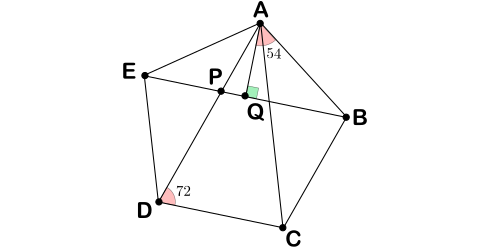
Informar de error en enunciado Informar de procedencia del problema
El área del triángulo $AOB$ se puede calcular de dos maneras equivalentes: \[\tfrac{1}{2}AB\cdot OP=\mathrm{Area}(AOB)=\tfrac{1}{2}BO\cdot AO\,\mathrm{sen}(60^\circ)=\tfrac{\sqrt{3}}{4}BO\cdot AO.\] Multiplicando por $(1+\lambda)$ y usando que \begin{align*} AC&=AO+OC=(1+\lambda)AO=7,\\ PQ&=OP+OQ=(1+\lambda)OP=4\sqrt{3}, \end{align*} según la información del enunciado, la igualdad de áreas se puede reescribir como \[AB\cdot (1+\lambda)OP=\tfrac{\sqrt{3}}{2}BO\cdot (1+\lambda)AO\ \Leftrightarrow\ \frac{BO}{AB}=\frac{8}{7}.\] Ahora bien, el teorema del coseno aplicado al triángulo $AOB$ nos dice que \[AB^2=BO^2+AO^2-2BO\cdot AO\cos(60^\circ)=BO^2+AO^2-BO\cdot AO,\] Dividiendo por $AB^2$, esto puede reescribirse como \[1=\left(\frac{BO}{AB}\right)^2+\left(\frac{AO}{AB}\right)^2-\frac{BO}{AB}\cdot \frac{AO}{AB}.\] Sustituyendo $\frac{BO}{AB}=\frac{8}{7}$ nos queda una ecuación de segundo grado en la incógnita $\frac{AO}{AB}$, que se resuelve fácilmente dando dos soluciones positivas: $\frac{AO}{AB}=\frac{3}{7}$ y $\frac{AO}{AB}=\frac{5}{7}$. Teniendo en cuenta que $AO=\frac{7}{1+\lambda}$, las soluciones anteriores nos dan $(1+\lambda)AB=\frac{49}{3}$ o bien $(1+\lambda)AB=\frac{49}{5}$.
Finalmente, como el área del trapecio está dada por $S=\frac{1}{2}(AB+CD)PQ=\frac{1}{2}(1+\lambda)AB\cdot PQ$ y que $PQ=4\sqrt{3}$ es conocido, llegamos a que las posibles soluciones son \[S=\frac{98\sqrt{3}}{3}\quad\text{y}\quad S=\frac{98\sqrt{3}}{5}.\] Las dos soluciones se corresponden con que $C$ se proyecte sobre $AB$.

Informar de error en enunciado Informar de procedencia del problema
- Si $\mathrm{sen}(\alpha)=\mathrm{sen}(\beta)$ y $\mathrm{sen}(\gamma)=\mathrm{sen}(\delta)$, hay dos posibilidades. La primera es que $\alpha+\beta=180^\circ$ o $\beta+\delta=180^\circ$ (en cuyo caso, $P$ está en la diagonal $AC$ o $BD$, respectivamente). La segunda es que $\alpha=\beta$ y $\gamma=\delta$; como $\alpha+\beta+\gamma+\delta=360^\circ$, se tiene que $\alpha+\delta=180^\circ$ y $P$ está sobre $BD$.
- Si $\mathrm{sen}(\alpha)=\mathrm{sen}(\delta)$ y $\mathrm{sen}(\gamma)=\mathrm{sen}(\beta)$, se razona de forma totalmente análoga.
Informar de error en enunciado Informar de procedencia del problema
Nota. Hemos usado la identidad de factorización \[\mathrm{sen}(x)\mathrm{sen}(y)=\frac{\cos(x-y)-\cos(x+y)}{2},\] que se deduce fácilmente sumando las fórmulas de los cosenos de la suma y la diferencia.
Informar de error en enunciado Informar de procedencia del problema