Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2764 problemas y 1057 soluciones.
Problema 1021
¿Qué valores han de tener los ángulos $\alpha$, $\beta$ y $\gamma$ de un triángulo $T$ para que este se pueda dividir en tres triángulos congruentes entre sí?
pistasolución 1info
Pista. Observa que si para subdividir unimos un vértice con un punto del lado opuesto, entonces necesariamente este segmento tiene que ser perpendicular al lado.
Solución. Hay cuatro formas esencialmente distintas de dividir un triángulo en tres triángulos, que está indicadas en la figura de abajo. Sin embargo, nos damos cuenta de que si un segmento termina en el interior de un lado y no es perpendicular a dicho lado, entonces forma dos ángulos suplementarios distintos. Estos dos ángulos deben ser dos de los ángulos de cada triángulo semejante pero un triángulo no puede tener dos ángulos que sumen $180^\circ$. Esto descarta directamente los casos III y IV y restringe el caso II. Veamos directamente qué restricciones adicionales nos da el hecho de que los tres triángulos deben tener ángulos iguales.
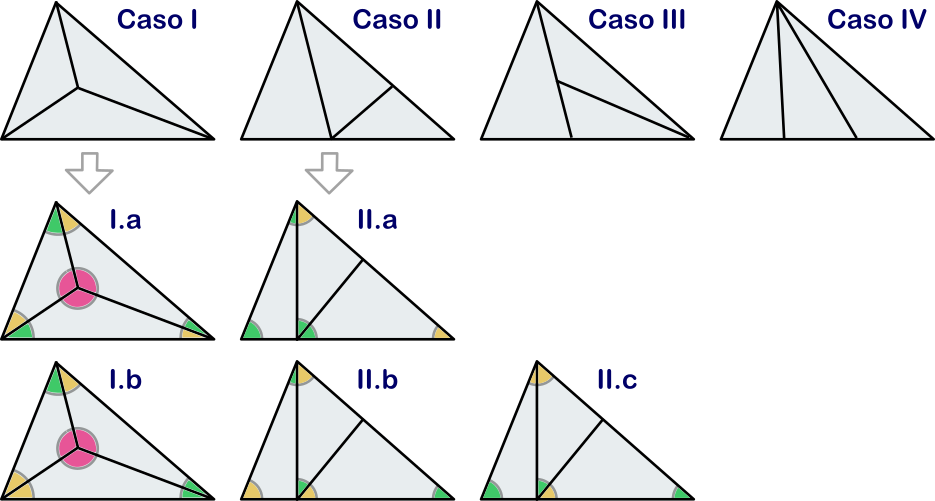
- Caso I. Tenemos un vértice interior, en el que se forman al menos dos ángulos obtusos, que deben ser iguales, y el tercero debe ser igual también ya que suma con uno de los obtusos más de $180^\circ$. Hay dos posibles configuraciones para los otros seis ángulos de los tres triángulos, que hemos llamado casos I.a y I.b. En el caso I.a, como la suma de los ángulos de $T$ es $180^\circ$, llegamos a que el ángulo verde más el amarillo suman $60^\circ$, luego $T$ es equilátero. En el caso I.b, el triángulo $T$ es isósceles, luego los ángulos amarillo y verde deben coincidir y también llegamos a que $T$ es equilátero.
- Caso II. Hay esencialmente tres configuraciones para los ángulos que no son rectos, que se indican en los casos II.a, II.b y II.c. En el caso II.a, dos verdes suman $90^\circ$, de donde se tiene que tanto el verde como el amarillo deben ser $45^\circ$ y $T$ es un triángulo rectángulo isósceles. En el caso II.b, el verde y el amarillo suman $90^\circ$, luego $T$ es en principio un triángulo rectángulo cualquiera. En el caso II.c, tenemos que $T$ es un triángulo isósceles cualquiera.
Tenemos, por tanto, que los únicos triángulos que pueden admitir la subdivisión son los triángulos rectángulos y los triángulos isósceles. Sin embargo, las subdivisiones que nos salen nos dan triángulos congruentes solamente en el caso del triángulo equilátero. Subdividiendo este último uniendo cada vértice con el centro, confirmamos que los triángulos equiláteros son las únicas soluciones.

Nota. Hemos probado, de hecho, que los únicos triángulos que se pueden subdividir en tres triángulos semejantes son los triángulos rectángulos y los triángulos isósceles.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 1020
Sea $E$ una elipse y consideremos tres rectas paralelas $r_1$, $r_2$ y $r_3$, cada una de las cuales corta a $E$ en dos puntos distintos. Sean estos puntos $A_1,B_1$, $A_2,B_2$ y $A_3,B_3$, respectivamente. Probar que los puntos medios de los segmentos $A_1B_1$, $A_2B_2$ y $A_3B_3$ están alineados.
pistasolución 1info
Pista. Puedes suponer en coordenadas que la elipse tiene ecuación
\[\frac{x^2}{a^2}+\frac{y^2}{b^2=1\]
y cortarla con rectas paralelas $y=mx+n$ dejando $m$ fijo y variando $n$.
Solución. Trabajando en coordenadas podemos suponer que el centro de $E$ es el origen de coordenadas y que sus semiejes están contenidos en los ejes de coordenadas, luego la elipse tiene ecuación
\[\frac{x^2}{a^2}+\frac{y^2}{b^2}=1,\]
donde $a,b\gt 0$ son las longitudes de los semiejes. Si cortamos esta elipse por un haz de rectas paralelas al eje $OY$, por simetría los puntos medios de los segmentos que se determinan están contenidos en el eje $OX$, luego están alineados. Vamos a ver que esto también es cierto para cualquier haz de rectas paralelas no verticales, es decir, veremos que los puntos medios de los segmentos determinado por la intersección de $E$ con las rectas forman una recta al dejar fija la pendiente $m\in\mathbb{R}$ y variar la ordenada en el origen $n\in\mathbb{R}$. Para hallar los puntos de intersección, sustituimos $y=mx+n$ en la ecuación de $E$, lo que nos da
\[\frac{x^2}{a^2}+\frac{(mx+n)^2}{b^2}=1\ \Leftrightarrow\ \left(\frac{1}{a^2}+\frac{m^2}{b^2}\right)x^2+\frac{2mn}{b^2}x+\left(\frac{n^2}{b^2}-1\right)=0.\]
Si la recta corta a $E$ en dos puntos $(x_1,y_1)$ y $(x_2,y_2)$, entonces $x_1$ y $x_2$ son las soluciones de la ecuación cuadrática anterior, luego la primera coordenada del punto medio que estamos buscando puede calcularse a partir de las relaciones de Cardano-Vieta para este polinomio (ver la nota):
\[\frac{x_1+x_2}{2}=\frac{1}{2}\cdot\frac{-\frac{2mn}{b^2}}{\frac{1}{a^2}+\frac{m^2}{b^2}}=\frac{-m}{b^2+a^2m^2}n,\]
y la segunda coordenada del punto medio será
\[\frac{y_1+y_2}{2}=\frac{m(x_1+x_2)}{2}+n=\frac{-m^2n}{2(b^2+a^2m^2)}+n=\left(\frac{-m^2}{2(b^2+a^2m^2)}+1\right)n.\]
Cuando $m$ está fijo, ambas coordenadas son de la forma
constante por $n$, luego forman una recta (que pasa por el origen) al variar $n$ y hemos terminado.
Nota. Hemos usado concretamente que en una ecuación $ax^2+bx+c=0$, la suma de las soluciones es $\frac{-b}{a}$.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 1018
OIM, 2016-P5
Las circunferencias $\mathcal C_1$ y $\mathcal C_2$ se cortan en dos puntos distintos $A$ y $K$. La tangente común a $\mathcal C_1$ y $\mathcal C_2$ más cercana a $K$ toca a $\mathcal C_1$ en $B$ y a $\mathcal C_2$ en $C$. Sean $P$ el pie de la perpendicular desde $B$ sobre $AC$ y $Q$ el pie de la perpendicular desde $C$ sobre $AB$. Si $E$ y $F$ son los puntos simétricos de $K$ respecto de las rectas $PQ$ y $BC$, probar que los puntos $A$, $E$ y $F$ son colineales.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 1016
OIM, 2016-P3
Sea $ABC$ un triángulo acutángulo cuya circunferencia circunscrita es $\Gamma$. Las tangentes a $\Gamma$ por $B$ y $C$ se cortan en $P$. Sobre el arco $AC$ que no contiene a $B$ se toma un punto $M$ distinto de $A$ y $C$, tal que la recta $AM$ corta a la recta $BC$ en $K$. Sean $R$ el punto simétrico de $P$ con respecto a la recta $AM$ y $Q$ el punto de intersección de las rectas $RA$ y $PM$. Sean $J$ el punto medio de $BC$ y $L$ el punto donde la recta paralela por $A$ a la recta $PR$ corta a la recta $PJ$. Demostrar que los puntos $L$, $J$, $A$, $Q$ y $K$ están sobre una misma circunferencia.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 1010
Sea $A_1$ el punto diametralmente opuesto al vértice $A$ del triángulo $ABC$ en la circunferencia circunscrita y sea $A'$ el punto en el que la recta $AA_1$ corta al lado $BC$. La perpendicular a $AA'$ trazada por $A'$ corta a los lados $AB$ y $AC$ (o a sus prolongaciones) en $M$ y $N$, respectivamente.
Demostrar que los puntos $A$, $M$, $A_1$ y $N$ están en una circunferencia cuyo centro se encuentra en la altura desde $A$ en el triángulo $ABC$.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre