Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2764 problemas y 1057 soluciones.
Problema 1006
OME Local, 2016-P11
Sean $C$ y $C'$ dos circunferencias tangentes exteriores con centros $O$ y $O'$ y radios $1$ y $2$, respectivamente. Desde $O$ se traza una tangente a $C'$ con punto de tangencia en $P'$ y desde $O'$ se traza la tangente a $C$ con punto de tangencia en $P$ en el mismo semiplano que $P'$ respecto de la recta que pasa por $O$ y $O'$. Hallar el área del triángulo $OXO'$, donde $X$ es el punto de corte de $O'P$ y $OP'$.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 1003
Dos circunferencias $C$ y $C'$ son secantes en dos puntos $P$ y $Q$. La recta que une los centros corta a $C$ en $R$ y a $C'$ en $R'$, la que une $P$ y $R'$ corta a $C$ en $X\neq P$ y la que une $P$ y $R$ corta a $C'$ en $X'\neq P$. Supongamos además que los tres puntos $X$, $Q$ y $X'$ están alineados.
- Hallar el ángulo $\angle XPX$.
- Demostrar que $(d+r−r')(d-r+r')=rr'$, donde $d$ es la distancia entre los centros de las circunferencias y $r$ y $r'$ sus radios.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 1000
En un triángulo $ABC$ la bisectriz por $A$, la mediana por $B$ y la altura por $C$ son concurrentes y además la bisectriz por $A$ y la mediana por $B$
son perpendiculares. Si el lado $AB$ mide una unidad, hallar cuánto miden los
otros dos lados.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 998
Sea $ABC$ un triángulo rectángulo en $C$ no isósceles con catetos $b\gt a$.
- Hallar el lado del cuadrado $AXYZ$ que circunscribe al triángulo $ABC$ (los vértices $B$ y $C$ tienen que estar en lados distintos del cuadrado).
- Explicar paso a paso cómo construir el cuadrado $AXYZ$ con regla y compás.
pistasolución 1info
Pista. Observa que $ACZ$ y $BCY$ son triángulos semejantes.
Solución. En la figura hemos representado el triángulo $ABC$ inscrito en el cuadrado $AXYZ$. Como el triángulo es rectángulo en $C$, se tiene que $\angle YBC=90^\circ-\angle YCB=\angle ACZ$, luego los triángulos $BCY$ y $ACZ$ son semejantes. Si llamamos $\ell$ al lado del cuadrado, tendremos que $CZ=\sqrt{b^2-\ell^2}$ y $CY=\ell-CX$, luego la semejanza nos dice que
\begin{align*}
\frac{CY}{AZ}=\frac{BC}{AC}&\ \Leftrightarrow\ \frac{\ell-\sqrt{b^2-\ell^2}}{\ell}=\frac{a}{b}\ \Leftrightarrow\ 1-\sqrt{\frac{b^2}{\ell^2}-1}=\frac{a}{b}\\
&\ \Leftrightarrow\ \sqrt{\frac{b^2}{\ell^2}-1}=1-\frac{a}{b}\ \Leftrightarrow\ \frac{b^2}{\ell^2}=1+\left(1-\frac{a}{b}\right)^2\\
&\ \Leftrightarrow\ \frac{1}{\ell^2}=\frac{b^2+(b-a)^2}{b^4}\ \Leftrightarrow\ \ell=\frac{b^2}{\sqrt{2b^2-2ab+a^2}}.
\end{align*}
Para construir el cuadrado observamos que al rotar el triángulo $90^\circ$ en sentido horario y antihorario (como se muestra en la figura) con centro en $A$, obtenemos triángulos congruentes $AB'C'$ y $AB''C''$. El cuadrado $AXYZ$ se convierte en sendos cuadrados con un lado en común con él, luego las rectas $BC'$ y $CB''$ contienen a los lados del cuadrado. Ahora basta tomar $Y$ como su intersección y $X$ y $Z$ como los pies de las perpendiculares desde $A$.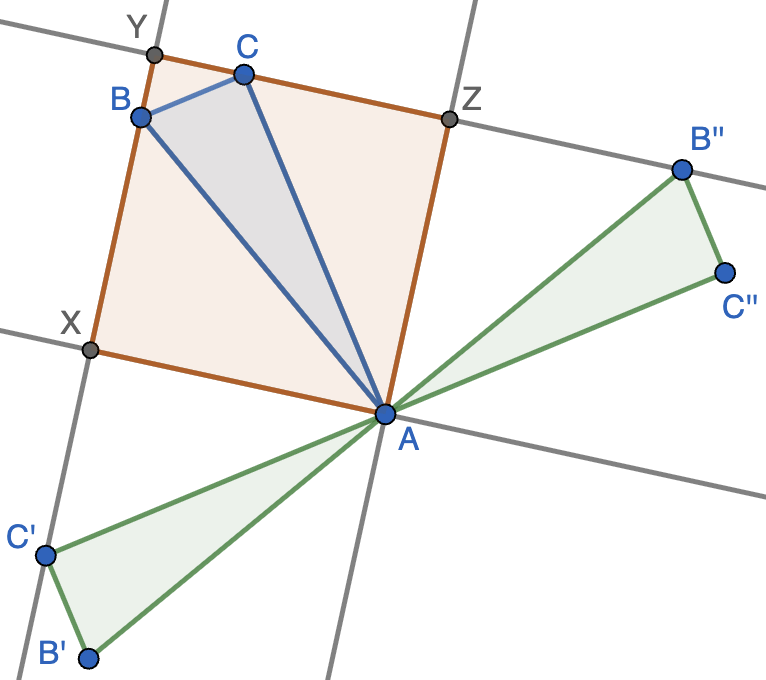

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 993
OIM, 2015-P4
En el triángulo acutángulo $ABC$, el punto $D$ es el pie de la perpendicular desde $A$ sobre el lado $BC$. Sea $P$ un punto del segmento $AD$. Las rectas $BP$ y $CP$ cortan a los lados $AC$ y $AB$ en $E$ y $F$, respectivamente. Sean $J$ y $K$ los pies de las perpendiculares desde $E$ y $F$ sobre $AD$, respectivamente. Demostrar que $FK=EJ$.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre