Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2748 problemas y 1042 soluciones.
Problema 946
Sea $ABCD$ un cuadrilátero convexo tal que
\[AB+CD=\sqrt{2}\,AC\qquad\text{y}\qquad BC+DA=\sqrt{2}\,BD.\]
¿Qué forma tiene dicho cuadrilátero?
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 941
OME Local, 2013-P12
Sean $A$, $B$ y $C$ los vertices de un triángulo y $P$, $Q$ y $R$ los respectivos pies de las bisectrices trazadas desde esos mismos vértices. Sabiendo que $PQR$ es un triángulo rectángulo en $P$, demostrar las siguientes afirmaciones:
- $ABC$ es obtusángulo.
- En el cuadrilátero $ARPQ$, pese a no ser cíclico, la suma de sus ángulos opuestos es constante.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 935
Por los puntos medios de dos lados de un triángulo $ABC$ trazamos las medianas y unimos los puntos que trisecan el tercer lado con el vértice opuesto. Así, en el interior del triángulo se obtiene una pajarita (dos
triángulos unidos por un vértice). Se pide calcular la fracción del área total del triangulo que representa la pajarita.
Sin pistas
Sin soluciones
infoSolución. Hola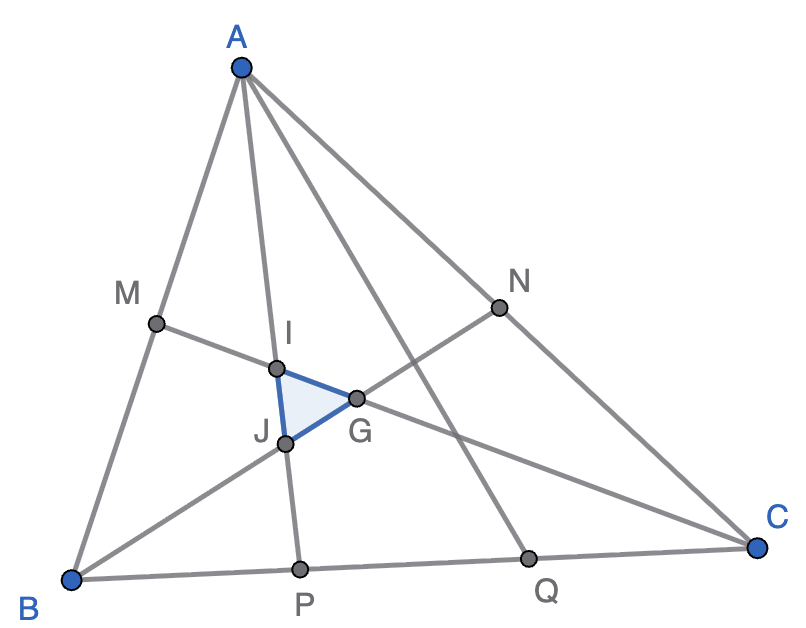

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 932
Deslizamos un cuadrado de $10\text{cm}$ de lado por el plano $OXY$ de forma que los vértices de uno de sus lados estén siempre en contacto con los ejes de coordenadas, uno con el eje $OX$ y otro con el eje $OY$. Determina los lugares geométricos que en ese movimiento describen:
- El punto medio del lado de contacto con los ejes.
- El centro del cuadrado.
- Los vértices del lado de contacto y del opuesto en el primer cuadrante.
pistasolución 1info
Pista. Utiliza coordenadas. En algún momento vas a tener que saber reconocer por su ecuación una cónica cuyos ejes no son paralelos a los ejes de coordenadas.
Solución. Por la simetría del problema, podemos pensar en que los puntos de contacto con los ejes están en el semiplano superior y luego añadir la configuración simétrica respecto del origen para completar los lugares geométricos que nos piden. Supondremos entonces que los vértices de contacto tienen coordenadas $A=(a,0)$ y $B=(0,\sqrt{100-a^2})$ y que, por tanto, $a$ se mueve en el intervalo $(-10,10)$. Observemos que $a=-10$ se corresponde con el cuadrado apoyado en el semieje negativo $OX$ y que el cuadrado está contenido en el tercer cuadrante, mientras que si $a=10$ entonces el cuadrado estará contenido completamente en el primer cuadrante.
- El punto medio $M$ del lado $AB$ tiene coordenadas $x_M=\tfrac{a}{2}$ e $y_M=\tfrac{1}{2}\sqrt{100-a^2})$, luego se cumple que $x_M^2+y_M^2=25$. Esto nos dice que $M$ describe la mitad superior de la circunferencia de radio $5$ y centro $(0,0)$. Por simetría, $M$ describe la circunferencia entera cuando dejamos que $B$ también se mueva por el semiplano inferior.
- Un vector normal al lado de contacto es $\vec{n}=(\sqrt{100-a^2},a)$ y tiene módulo $10$ igual a la longitud del lado. El centro del cuadrado puede calcularse como $C=M+\frac{1}{2}\vec{n}$, que tiene coordenadas $x_C=\tfrac{a}{2}+\frac{1}{2}\sqrt{100-a^2}$ e $y_C=\tfrac{1}{2}\sqrt{100-a^2})+\frac{a}{2}$, por lo que se cumple que $x_C=y_C$. Queda por ver qué puntos exactamente de la recta $x=y$ (bisectriz del primer cuadrante) toma el punto $C$, para lo que consideramos la función $f(a)=\tfrac{a}{2}+\frac{1}{2}\sqrt{100-a^2}$, que es continua en $[-10,10]$ y derivable en $(-10,10)$. Se verifica que $f'(a)=\frac{1}{2}-\frac{x}{2\sqrt{100-x^2}}$, de donde es fácil ver que $f'(a)=0$ tiene por única solución $a=5\sqrt{2}$, donde la función alcanza su máximo absoluto en el intervalo $[-10,10]$ y el valor máximo correspondiente es $f(5\sqrt{2})=5\sqrt{2}$. El mínimo absoluto se alcanza en el extremo $a=-10$, donde no es derivable, pero se cumple que $f(-10)=-5$. De esta forma, $C$ toma todos los valores en el segmento que une $(-5,-5)$ y $(5\sqrt{2},5\sqrt{2})$. Al considerar también el caso simétrico en que $B$ recorre el semiplano inferior, concluimos que el lugar geométrico de $C$ es el segmento rectilíneo que une $(-5\sqrt{2},-5\sqrt{2})$ y $(5\sqrt{2},5\sqrt{2})$ contenido en la bisectriz del primer cuadrante, incluyendo los extremos de dicho segmento.
- Un vértice $V$ opuesto al lado $AB$ viene dado por $V=A+\vec{n}$, luego tiene coordenadas $x_V=a+\sqrt{100-a^2}$ e $y_V=a$. Tenemos así que $(x_V-y_V)^2=100-y_V^2$ o equivalentemente $x_V^2-2x_Vy_V+2y_V^2=100$. Se trata, por tanto, de saber qué conjunto representa la ecuación $x^2-2xy+2y^2=100$. Como es un polinomio cuadrático, deducimos que se trata de una cónica; como podemos completar cuadrados para expresarlo como $(x-y)^2+y^2=100$ y ambos cuadrados tienen coeficientes positivos, deducimos que se trata de una elipse; como no tiene términos lineales en $x$ o $y$, deducimos que está centrada en el origen, aunque no tiene sus ejes paralelos a los ejes de coordenadas por tener término en $xy$. Ahora bien, al variar $a$ en $[-10,10]$ se ve fácilmente que se recorren todos los puntos de la elipse una vez se ha añadido el caso en que $B$ recorre el semieje $OY$ negativo.
Nota. Hemos supuesto que cuando $A$ y $B$ están en los semiejes positivos, el cuadrado está enteramente contenido en el primer cuadrante. Existe otra posibilidad que es suponer que en ese caso el cuadrado mira hacia el otro lado. No obstante, en tal caso, los lugares geométricos que nos piden serían simétricos de los obtenidos ya que se trataría simplemente de girar $90^\circ$ la figura.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 928
OIM, 2012-P5
Sea $ABC$ un triángulo y sean $P$ y $Q$ los puntos de intersección de la recta paralela a $BC$ que pasa por $A$ con las bisectrices exteriores de los ángulos $\angle B$ y $\angle C$, respectivamente. La perpendicular a $BP$ por $P$ y la perpendicular a $CQ$ por $Q$ se intersecan en $R$. Si $I$ es el incentro de $ABC$, mostrar que $AI=AR$.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre