Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2764 problemas y 1057 soluciones.
Problema 950
OIM, 2013-P4
Sean $\Gamma$ una circunferencia de centro $O$, $AE$ un diámetro de $\Gamma$ y $B$ el punto medio de uno de los arcos $AE$ de $\Gamma$. El punto $D\neq E$ está sobre el segmento $OE$. El punto $C$ es tal que el cuadrilátero $ABCD$ es un paralelogramo con $AB$ paralelo a $CD$ y $BC$ paralelo a $AD$. Las rectas $EB$ y $CD$ se cortan en el punto $F$. La recta $OF$ corta al arco menor $EB$ de $\Gamma$ en el punto $I$. Demostrar que la recta $EI$ es la bisectriz del ángulo $\angle BEC$.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 948
OIM, 2013-P2
Sean $X$ e $Y$ los extremos de un diámetro de una circunferencia $\Gamma$ y $N$ el punto medio de uno de los arcos $XY$ de $\Gamma$. Sean $A$ y $B$ dos puntos en el segmento $XY$. Las rectas $NA$ y $NB$ cortan nuevamente a $\Gamma$ en los puntos $C$ y $D$, respectivamente. Las tangentes a $\Gamma$ en $C$ y $D$ se cortan en $P$. Sea $M$ el punto de intersección del segmento $XY$ con el segmento $NP$. Demostrar que $M$ es el punto medio del segmento $AB$.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 946
Sea $ABCD$ un cuadrilátero convexo tal que
\[AB+CD=\sqrt{2}\,AC\qquad\text{y}\qquad BC+DA=\sqrt{2}\,BD.\]
¿Qué forma tiene dicho cuadrilátero?
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 941
OME Local, 2013-P12
Sean $A$, $B$ y $C$ los vertices de un triángulo y $P$, $Q$ y $R$ los respectivos pies de las bisectrices trazadas desde esos mismos vértices. Sabiendo que $PQR$ es un triángulo rectángulo en $P$, demostrar las siguientes afirmaciones:
- $ABC$ es obtusángulo.
- En el cuadrilátero $ARPQ$, pese a no ser cíclico, la suma de sus ángulos opuestos es constante.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 935
Por los puntos medios de dos lados de un triángulo $ABC$ trazamos las medianas y unimos los puntos que trisecan el tercer lado con el vértice opuesto. Así, en el interior del triángulo se obtiene una pajarita (dos
triángulos unidos por un vértice). Se pide calcular la fracción del área total del triangulo que representa la pajarita.
Sin pistas
Sin soluciones
infoSolución. Hola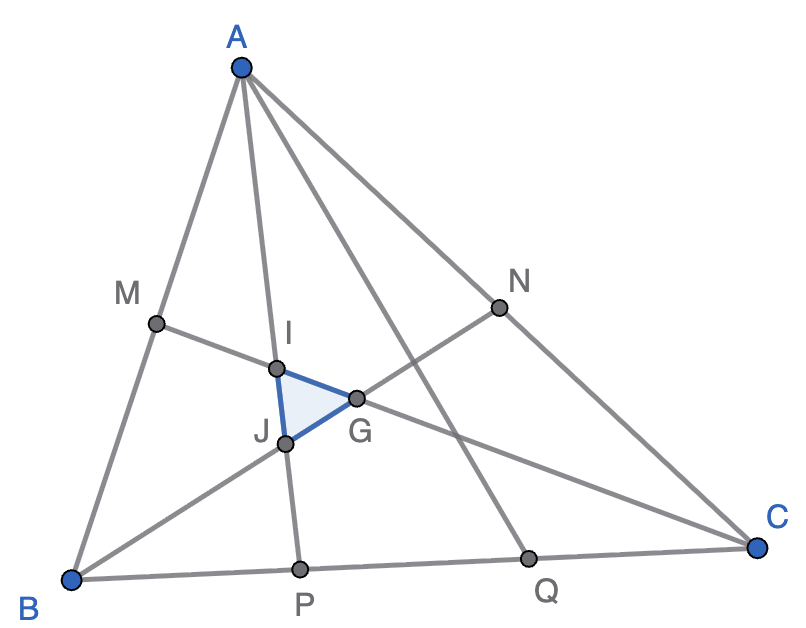

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre