Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2748 problemas y 1042 soluciones.
Problema 908
Sea $ABC$ un triángulo acutángulo con $\angle BAC=45^\circ$ y sea $P$ el pie de la altura que pasa por $B$. Trazamos la circunferencia de centro $P$ que pasa por $C$ y que vuelve a cortar a $AC$ en el punto $X$ y a la altura $PB$ en el punto $Y$. Sean $r$ y $s$ las rectas perpendiculares a la recta $AY$ por $P$ y $X$, respectivamente, y $L$ y $K$ las respectivas intersecciones de $r$ y $s$ con $AB$. Demostrar que $L$ es el punto medio de $KB$.
pistasolución 1info
Pista. Demuestra que $P$ es el ortocentro de $ABC$.
Solución. Como el triángulo $CXY$ es rectángulo isósceles, la recta $CY$ es perpendicular a $XY$ y por tanto también a $AB$ ($XY$ y $AB$ son paralelas ya que ambas forman un ángulo de $45^\circ$ con $AC$). Entonces, $CY$ es una altura del triángulo $ABC$ y, en consecuencia, $Y$ es el ortocentro del triángulo. En particular, deducimos que $AY$ es perpendicular a $CB$, luego $r$ y $s$ son paralelas a $CB$. Finalmente, el teorema de Thales nos asegura que $KL=LB$ a través de estas tres rectas paralelas ya que $XP=PC$.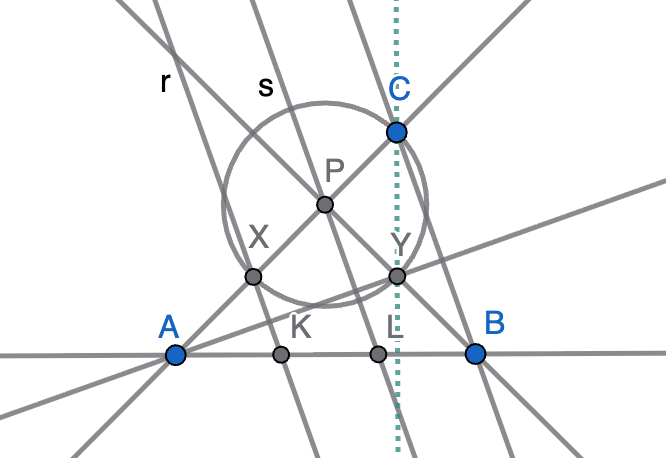

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 904
OIM, 2011-P4
Sea $ABC$ un triángulo acutángulo, con $AC\neq BC$, y sea $O$ su circuncentro. Sean $P$ y $Q$ puntos tales que $BOAP$ y $COPQ$ son paralelogramos. Demostrar que $Q$ es el ortocentro de $ABC$.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 903
OIM, 2011-P3
Sea $ABC$ un triángulo y sean $X,Y,Z$ los puntos de tangencia de su circunferencia inscrita con los lados $BC,CA,AB$, respectivamente. Supongamos que $C_1,C_2,C_3$ son circunferencias con cuerdas $YZ,ZX,XY$, respectivamente, tales que $C_1$ y $C_2$ se cortan sobre la recta $CZ$ y que $C_1$ y $C_3$ se corten sobre la recta $BY$. Suponga que $C_1$ corta a las cuerdas $XY$ y $ZX$ en $J$ y $M$, respectivamente; que $C_2$ corta a las cuerdas $YZ$ y $XY$ en $L$ e $I$, respectivamente; y que $C_3$ corta a las cuerdas $YZ$ y $ZX$ en $K$ y $N$, respectivamente. Demostrar que $I,J,K,L,M,N$ están sobre una misma circunferencia.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 898
Sea $ABC$ un triángulo con $\angle ABC=2\angle BCA$ y $\angle CAB\gt 90^\circ$. Sean $D$ el punto de la recta $AB$ tal que $CD$ es perpendicular a $AC$ y $M$ el punto medio de $BC$. Demostrar que $\angle AMB=\angle DMC$.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 897
Sean $A,B,C,D$ cuatro puntos en el espacio tales que no hay ningún plano que pasa por los cuatro a la vez. Los segmentos $AB$, $BC$, $CD$ y $DA$ son tangentes a una misma esfera. Demuestra que los cuatro puntos de tangencia están en un mismo plano.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre