Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2764 problemas y 1057 soluciones.
Problema 912
Sea $P$ un punto interior a un triángulo $ABC$ y sean $H_A$, $H_B$ y $H_C$ los ortocentros de los triángulos $PBC$, $PAC$ y $PAB$, respectivamente. Demostrar que los triángulos $H_AH_BH_C$ y $ABC$ tienen igual área.
pistasolución 1info
Pista. Demuestra que
\[\text{Área}PH_AH_B)=\pm\text{Área}(ABC)\cot(\angle BPC)\cot(\angle APC)\]
para lo que puede ser útil considerar que el área de un triángulo es la mitad del producto de dos de sus lados y el seno del ángulo que forman.
Solución. Llamamos $\alpha,\beta,\gamma$ a los ángulos del triángulo $ABC$ y también consideramos los ángulos $x=\angle BPC$, $y=\angle CPA$ y $z=\angle APB$. Nos centraremos en el triángulo $PH_AH_B$ por el momento. Su área se puede calcular como
\[\text{Área}(PH_AH_B)=\tfrac{1}{2}PH_A\cdot PH_B\,\mathrm{sen}\,\angle H_APH_B.\qquad (\star)\]
Ahora bien, $PH_A$ es la distancia de un vértice al ortocentro en el triángulo $PBC$ y por tanto igual al doble de la distancia del circuncentro $O_A$ de $PBC$ al punto medio $M$ del lado opuesto $BC$. Distinguimos dos casos:
- Si $x\geq 90$, entonces la propiedad del arco central en la circunferencia circunscrita a $ABP$ nos dice que $\angle BO_AM=180-x$, con lo que en el triángulo rectángulo $BO_AM$ tenemos que $PH_A=BC\cot(180-x)=-BC\cot(x)$.
- Si $x\lt 90$, entonces un razonamiento similar nos dice que $PH_A=BC\cot(x)$.
- Si $x$ es obtuso, entonces los tres puntos $H_A,H_B,H_C$ están fuera de los triángulos de los que son ortocentros, luego $P$ es interior a $H_AH_BH_C$ y se tiene que $\text{Área}(H_AH_BH_C)$ es la suma de las áreas $\text{Área}(PH_AH_B)$, $\text{Área}(PH_BH_C)$ y $\text{Área}(PH_CH_A)$. Esto también se extiende al caso en que $x$ es recto, ya que se tendría que $P$ coincide con uno de los vértices de $H_AH_BH_C$ y dos de las áreas anteriores serían nulas. En ambos casos, como las cotangentes de $x,y,z$ son todas menores o iguales que cero, tenemos que \begin{align*} \text{Área}(H_AH_BH_C)&=\text{Área}(ABC)(\cot(x)\cot(y)+\cot(y)\cot(z)+\cot(z)\cot(x)\\ &=\text{Área}(ABC)\bigl(\cot(x)\cot(y)+(\cot(x)+\cot(y))\cot(360-x-y)\bigr)\\ &=\text{Área}(ABC)\bigl(\cot(x)\cot(y)-(\cot(x)+\cot(y))\cot(x+y)\bigr) \\ &=\text{Área}(ABC)\left(\cot(x)\cot(y)-(\cot(x)+\cot(y))\frac{\cot(x)\cot(y)-1}{\cot(x)+\cot(y)}\right)\\ &=\text{Área}(ABC). \end{align*}
- Si $x$ es agudo, el razonamiento es similar, solo que ahora hay que restar del área de $PH_BH_C$ las áreas de $PH_CH_A$ y $PH_AH_B$. Sin embargo, estos cambios de signo se cancelan con los cambios de signo de la cotangente de $x$ y se puede seguir al pie de la letra el cálculo del apartado anterior.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 908
Sea $ABC$ un triángulo acutángulo con $\angle BAC=45^\circ$ y sea $P$ el pie de la altura que pasa por $B$. Trazamos la circunferencia de centro $P$ que pasa por $C$ y que vuelve a cortar a $AC$ en el punto $X$ y a la altura $PB$ en el punto $Y$. Sean $r$ y $s$ las rectas perpendiculares a la recta $AY$ por $P$ y $X$, respectivamente, y $L$ y $K$ las respectivas intersecciones de $r$ y $s$ con $AB$. Demostrar que $L$ es el punto medio de $KB$.
pistasolución 1info
Pista. Demuestra que $P$ es el ortocentro de $ABC$.
Solución. Como el triángulo $CXY$ es rectángulo isósceles, la recta $CY$ es perpendicular a $XY$ y por tanto también a $AB$ ($XY$ y $AB$ son paralelas ya que ambas forman un ángulo de $45^\circ$ con $AC$). Entonces, $CY$ es una altura del triángulo $ABC$ y, en consecuencia, $Y$ es el ortocentro del triángulo. En particular, deducimos que $AY$ es perpendicular a $CB$, luego $r$ y $s$ son paralelas a $CB$. Finalmente, el teorema de Thales nos asegura que $KL=LB$ a través de estas tres rectas paralelas ya que $XP=PC$.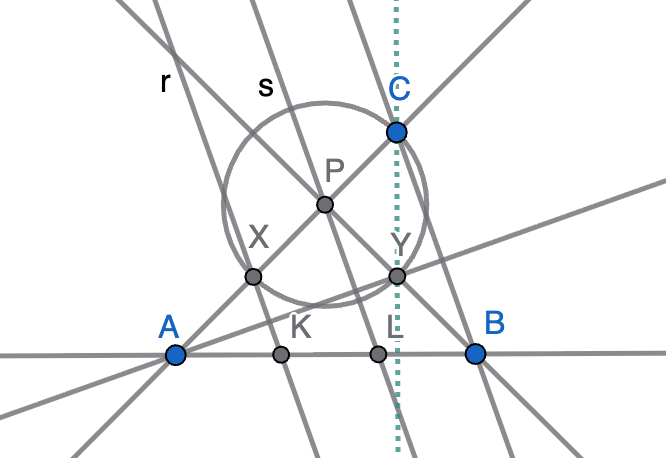

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 904
OIM, 2011-P4
Sea $ABC$ un triángulo acutángulo, con $AC\neq BC$, y sea $O$ su circuncentro. Sean $P$ y $Q$ puntos tales que $BOAP$ y $COPQ$ son paralelogramos. Demostrar que $Q$ es el ortocentro de $ABC$.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 903
OIM, 2011-P3
Sea $ABC$ un triángulo y sean $X,Y,Z$ los puntos de tangencia de su circunferencia inscrita con los lados $BC,CA,AB$, respectivamente. Supongamos que $C_1,C_2,C_3$ son circunferencias con cuerdas $YZ,ZX,XY$, respectivamente, tales que $C_1$ y $C_2$ se cortan sobre la recta $CZ$ y que $C_1$ y $C_3$ se corten sobre la recta $BY$. Suponga que $C_1$ corta a las cuerdas $XY$ y $ZX$ en $J$ y $M$, respectivamente; que $C_2$ corta a las cuerdas $YZ$ y $XY$ en $L$ e $I$, respectivamente; y que $C_3$ corta a las cuerdas $YZ$ y $ZX$ en $K$ y $N$, respectivamente. Demostrar que $I,J,K,L,M,N$ están sobre una misma circunferencia.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 898
Sea $ABC$ un triángulo con $\angle ABC=2\angle BCA$ y $\angle CAB\gt 90^\circ$. Sean $D$ el punto de la recta $AB$ tal que $CD$ es perpendicular a $AC$ y $M$ el punto medio de $BC$. Demostrar que $\angle AMB=\angle DMC$.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre