Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
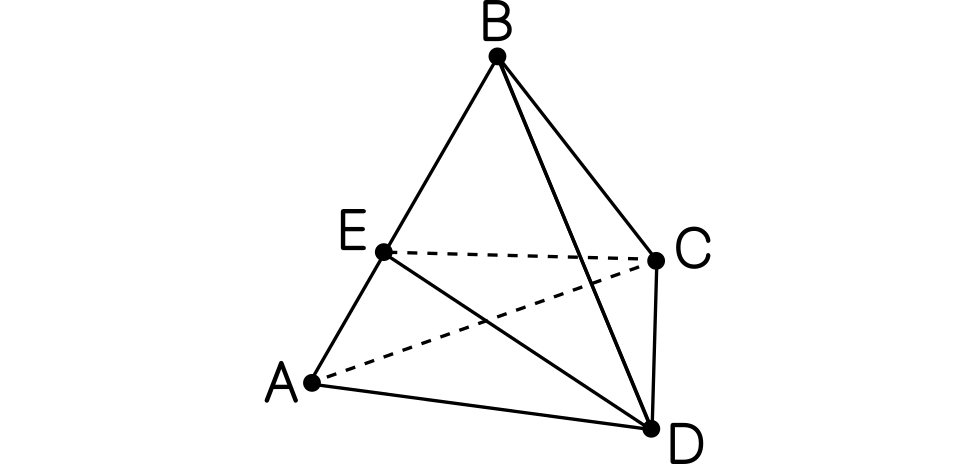
Nota. Usando el seno en lugar de la tangente, también puede razonarse de forma similar que lo que hay que minimizar es la longitud de $CE$, lo que nos lleva a que ha de ser perpendicular a $AC$ y $E$ tiene que ser el punto medio.
Informar de error en enunciado Informar de procedencia del problema
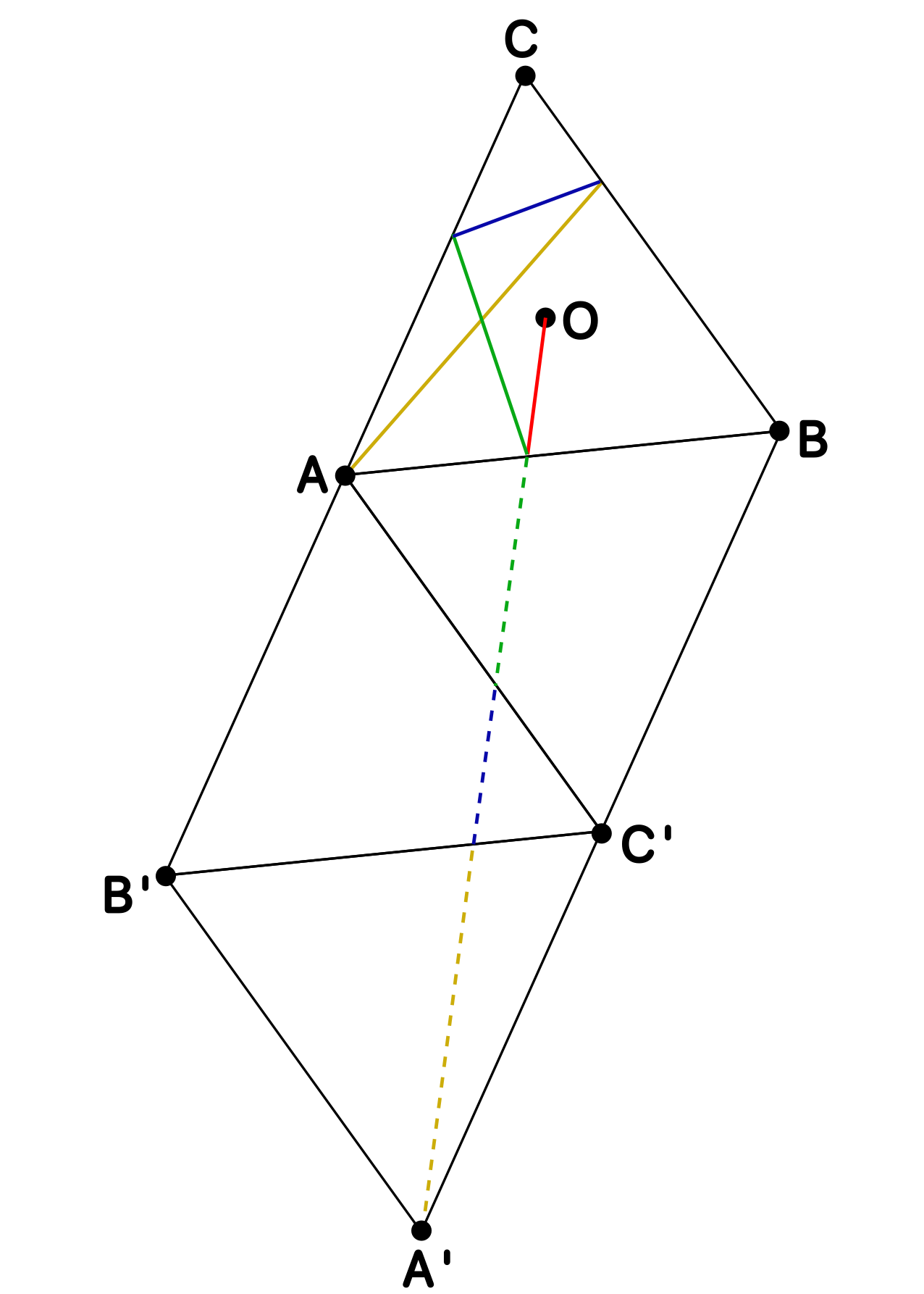
Nota. Cuando un rayo se refleja en un lado, los ángulos de entrada (incidencia) y salida (reflexión) coinciden.

Para ello, observamos que $OBA'$ es un triángulo rectángulo ya que $OB$ es una altura del triángulo equilátero y $BA'$ es paralela al lado opuesto. Además, se tiene que $OB=\frac{2}{3}\cdot\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{3}$ (dos tercios de la altura) y $BA'=2$ (dos veces el lado), luego el teorema de Pitágoras nos da la distancia que buscamos: \[OA'=\sqrt{\left(\tfrac{\sqrt{3}}{3}\right)^2+2^2}=\frac{\sqrt{39}}{3}.\]
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema