Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2764 problemas y 1057 soluciones.
Problema 882
OIM, 2010-P5
Sea $ABCD$ un cuadrilátero cíclico cuyas diagonales $AC$ y $BD$ son perpendiculares. Sean $O$ el circuncentro de $ABCD$, $K$ la intersección de sus diagonales, $L\neq O$ la intersección de las circunferencias circunscritas a $OAC$ y $OBD$, y $G$ la intersección de las diagonales del cuadrilátero cuyos vértices son los puntos medios de $ABCD$. Probar que $O$, $K$, $L$ y $G$ están alineados.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 880
OIM, 2010-P3
La circunferencia $\Gamma$ inscrita al triángulo escaleno $ABC$ es tangente a los lados $BC$, $CA$ y $AB$ en los puntos $D$, $E$ y $F$, respectivamente. La recta $EF$ corta a la recta $BC$ en $G$. La circunferencia de diámetro $GD$ corta a $\Gamma$ en $R$ ($R\neq D$). Sean P y Q ($P\neq R$, $Q\neq R$) las intersecciones de $BR$ y $CR$ con $\Gamma$, respectivamente. Las rectas $BQ$ y $CP$ se cortan en $X$. La circunferencia circunscrita a $CDE$ corta al segmento $QR$ en $M$ y la circunferencia circunscrita a $BDF$ corta al segmento $PR$ en $N$. Demostrar que las rectas $PM$, $QN$ y $RX$ son concurrentes.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 877
Sea $P$ un punto cualquiera de la bisectriz del ángulo $A$ de un triángulo $ABC$ y sean $A',B',C'$ puntos de las rectas $BC,CA,AB$, respectivamente, tales que $PA'$ es perpendicular a $BC$, $PB'$ es perpendicular a $CA$ y $PC'$ es perpendicular a $AB$. Demostrar que $PA'$ y $B'C'$ se cortan sobre la mediana $AM$, siendo $M$ el punto medio de $BC$.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 875
Sea $ABCD$ un cuadrilátero convexo y sea $P$ la intersección de sus diagonales $AC$ y $BD$ y supongamos que cumple $\angle APD=60^\circ$. Sean $E,F,G,H$ los puntos medios de los lados $AB,BC,CD,DA$, respectivamente. Hallar el mayor número real positivo $k$ tal que
\[EG+3HF\geq kd+(1-k)s,\]
siendo $s$ el semiperímetro de $ABCD$ y $d$ la suma de las longitudes de las diagonales.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 869
Se considera un tetraedro regular como el de la figura. Si el punto $E$ recorre la arista $AB$. ¿Cuándo el ángulo $\angle CED$ es máximo?
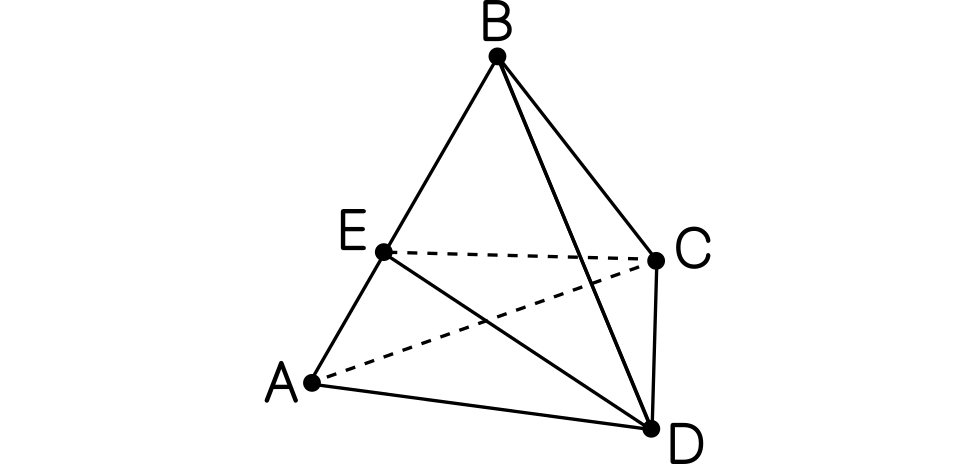
pistasolución 1info
Pista. Si $M$ es el punto medio de $CD$, demuestra el ángulo será máximo cuando la longitud de $EM$ sea mínima.
Solución. Sea $M$ el punto medio de $CD$, de forma que $EM$ es una altura del triángulo isósceles $CDE$. El ángulo $\alpha=\angle CED$ verifica que $\mathrm{tan}(\frac{\alpha}{2})=\frac{CM}{EM}$. El ángulo será máximo cuando la tangente sea máxima, es decir, cuando $EM$ sea mínimo ya que $CM$ no depende de dónde hayamos puesto el punto $E$. Ahora podemos restringirnos al plano que contiene al triángulo $ABM$. El segmento $EM$ está en este plano y su longitud será mínima cuando $EM$ sea perpendicular a $AB$, es decir, cuando $EM$ sea una altura de $ABM$, que coincide con la mediatriz por ser $ABM$ isósceles. Concluimos que el ángulo $\angle CED$ es máximo cuando $E$ es el punto medio de $AB$.
Nota. Usando el seno en lugar de la tangente, también puede razonarse de forma similar que lo que hay que minimizar es la longitud de $CE$, lo que nos lleva a que ha de ser perpendicular a $AC$ y $E$ tiene que ser el punto medio.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre