Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
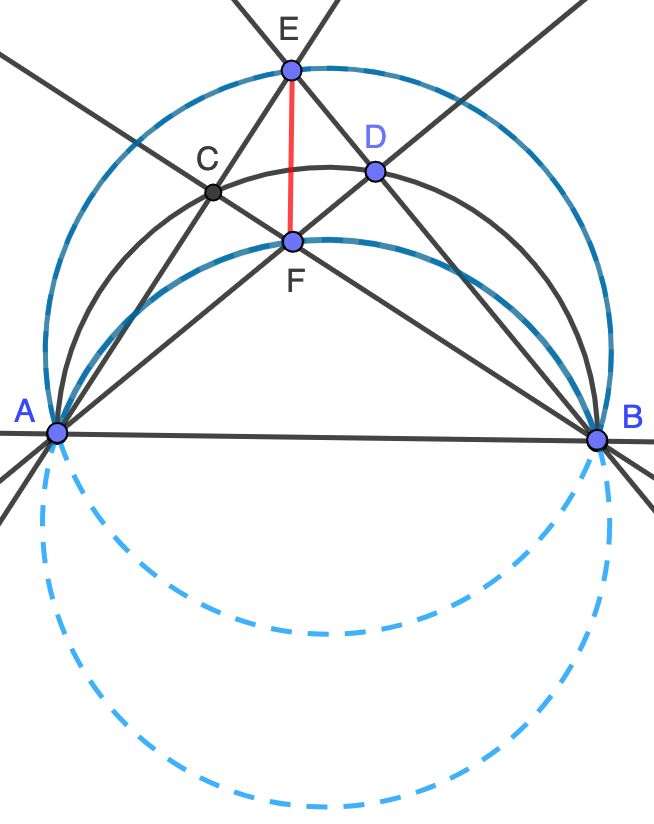
Es muy fácil darse cuenta de la recta $EF$ ha de ser perpendicular a $AB$: dado que los ángulos $\angle ACB$ y $\angle ADB$ son rectos por comprender al diámetro $AB$ en la semicircunferencia, se tiene que $AD$ y $BC$ son alturas del triángulo $AEB$, luego $F$ es su ortocentro y $EF$ es la tercera altura, que debe ser perpendicular al lado $AB$. Tenemos así que la dirección del segmento $EF$ no varía.
Veamos ahora que su longitud tampoco varía. Por la propiedad del arco capaz, el ángulo $\alpha=\angle CAD=\angle CBD$ sólo depende de $c$, no de la posición concreta de la cuerda $CD$. Como los ángulos $\angle ACB$ y $\angle ADB$ son rectos por comprender al diámetro $AB$ en la semicircunferencia, deducimos que $\angle AEB=90-\alpha$. Además, como la suma de los ángulos del cuadrilátero $ECFD$ es $360$, tenemos también que $\angle AFB=\angle CFD=90+\alpha$. Todo ello nos dice que los puntos $E$ y $F$ se mueven en sendos arcos de circunferencia con extremos $A$ y $B$ (al variar la cuerda $CD$ sin modificar su longitud), como puede verse en la figura. Además, como los ángulos con los que $E$ y $F$ ven al segmento $AB$ son $90-\alpha$ y $90+\alpha$, que suman $180$, estas circunferencias son simétricas respecto de $AB$. En particular, tienen el mismo radio y, al pasar por $A$ y $B$, tiene que ser una trasladada de la otra en la dirección perpendicular a $AB$. De esta forma, la longitud del segmento $EF$ es la del vector de traslación, o sea, constante.
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
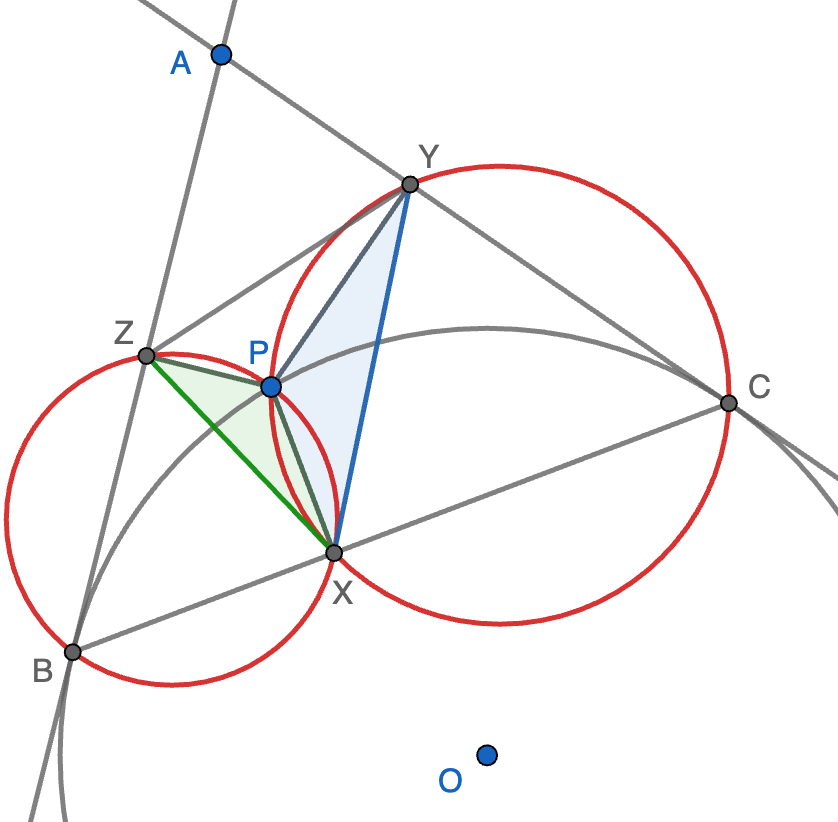
El primer caso es que $P$ sea interior al triángulo $ABC$. Los cuadriláteros $ZPBX$ e $YPXC$ son cíclicos ya que tienen dos ángulos rectos opuestos. La propiedad del arco capaz nos dice que $\angle XPY=180-\angle ACB$ y $\angle ZPX=180-\angle ABC$; como se tiene que $\angle ACB=\angle ABC$ por ser $ABC$ isósceles, se deduce que $\angle XPY=\angle ZPX$ y ya tenemos un ángulo igual. Para el segundo ángulo, calculamos de nuevo por arco capaz \begin{align*} \angle PXY-\angle ZPX&=\angle PCY-\angle PBX=\angle ACB-\angle PCX-\angle PBX\\ &=\angle ACB-180+\angle BPC. \end{align*} En el último paso hemos usado que los ángulos del triángulo $BPC$ suman $180$. Ahora bien, $\angle BOC=360-2\angle BPC$ por la propiedad del arco central, donde $O$ es el centro de la circunferencia tangente a los lados. Como en el cuadrilátero $ABCO$ los ángulos suman $360$ y dos de ellos son rectos, llegamos a que $\angle BOC=180-\angle BAC$ y, por tanto, $\angle BPC=90+\frac{1}{2}\angle BAC=180-\angle ACB$ (ya que $ABC$ es isósceles). Volviendo al cálculo anterior, tenemos que $\angle PXY-\angle ZPX=0$, lo que concluye la demostración de que $XPY$ es semejante a $ZPX$.
El segundo caso es que $P$ sea exterior al triángulo $ABC$, es decir, $P$ está en el arco mayor $BC$ de la circunferencia. La demostración se adapta pero los cálculos son ligeramente distintos. La igualdad $\angle XPY=\angle ZPX$ es cierta pero en este caso porque los dos ángulos son iguales a $180-\angle ABC$. Para la otra igualdad de ángulo, calculamos \begin{align*} \angle PXY-\angle ZPX&=\angle PCY-\angle PBX=180-\angle ACB-\angle PCX-\angle PBX\\ &=\angle ACB+\angle BPC=\angle ACB+\tfrac{1}{2}\angle BOC=\angle ACB+\tfrac{1}{2}(180-\angle BAC)=0. \end{align*}
Informar de error en enunciado Informar de procedencia del problema
- $0^\circ\leq A \leq 60^\circ$.
- La altura relativa al lado $a$ es tres veces el inradio $r$.
- La distancia del circuncentro al lado $a$ es $R-r$, siendo $R$ el circunradio.
En cuanto al apartado (b), calculamos el área del triángulo de dos formas distintas. Por un lado, $S=\frac{1}{2}(a+b+c)r$ y por otro $S=\frac{1}{2} ah_a$, siendo $h_a$ la altura relativa al vértice $A$. Sustituyendo $a=\frac{b+c}{2}$ en ambas expresiones e igualándolas, se llega directamente a que $h_a=3r$.
Finalmente, para el apartado (c) usaremos la fórmula $abc=4RS$ y la fórmula de Herón, de forma que \begin{align*} R-r&=\frac{abc}{4S}-\frac{2S}{a+b+c}=\frac{abc(a+b+c)-8S^2}{4(a+b+c)S}\\ &=\frac{abc(a+b+c)-\frac{1}{2}(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}{4(a+b+c)S}\\ &=\frac{2abc-(-a+b+c)(a-b+c)(a+b-c)}{8S}=\frac{(b+c)bc-\frac{b+c}{2}(\frac{-b+3c}{2})(\frac{3b-c}{2})}{8S}\\ &=\frac{(b+c)(3b^2-2bc+3c^2)}{64S}=\frac{abc\cos(A)}{4S}=R\cos(A). \end{align*} Si $O$ es el circuncentro y $M$ el punto medio de $BC$, entonces el triángulo $BOM$ es rectángulo y tiene $\angle COM=A$ ya que este es la mitad del ángulo central. Por tanto, en este triángulo rectángulo se cumple que $\cos(A)=\frac{OM}{OB}$, es decir, $OM=OB\cos(A)=R\cos(A)$ y hemos terminado.
Nota. Probablemente, la demostración del apartado (c) no sea la más elegante, pero es sistemática en el sentido de que expresamos $R-r$ en función únicamente de los lados $a,b,c$. Luego se puede expresar también $OM$ en términos de estos lados y usando la condición $a=\frac{b+c}{2}$ se tiene que conseguir probar el enunciado. En la solución propuesta, se ha introducido además el área y el coseno de $A$ como atajo para evitar más cálculos.
Informar de error en enunciado Informar de procedencia del problema